В последние десятилетия модели многомерных временных рядов, такие как модель векторной авторегрессии VAR , её модификации SVAR (структурная векторная авторегрессия) и BVAR (байесовская векторная авторегрессия), нашли широкое применение в макроэкономическом анализе при исследовании влияния шоков одних экономических переменных на другие [1, 2]. Этому способствовал ряд причин, в частности простота применения, по сравнению с системами одновременных уравнений, требующими выполнения априорных ограничений на структурные параметры для решения проблемы эндогенности регрессоров, точность результатов, сопоставимая с точностью сложных макроэкономических моделей, разработка аппарата оценивания, диагностики, исследования и его реализация в современных эконометрических пакетах, таких как Eviews, SAS, STATA, SPSS, и т.д., а также пакетах свободно распространяемых объектно-ориентированных языков программирования R и Piton.
Годовые значения макроэкономических показателей
|
№ |
год |
Y |
X |
№ |
год |
Y |
X |
|
1 |
1991 |
0,9 |
0,5 |
16 |
2006 |
17809,7 |
5698,8 |
|
2 |
1992 |
9,2 |
6,6 |
17 |
2007 |
21968,6 |
8034,1 |
|
3 |
1993 |
106,8 |
46,3 |
18 |
2008 |
27543,5 |
10526,1 |
|
4 |
1994 |
422,1 |
156 |
19 |
2009 |
29269,6 |
7344,8 |
|
5 |
1995 |
1016,6 |
363,4 |
20 |
2010 |
32514,6 |
10472,7 |
|
6 |
1996 |
1435,9 |
475,2 |
21 |
2011 |
40883,8 |
14584,1 |
|
7 |
1997 |
1776,1 |
514,8 |
22 |
2012 |
47273,4 |
16721,9 |
|
8 |
1998 |
2003,8 |
393,5 |
23 |
2013 |
52433,6 |
16985 |
|
9 |
1999 |
3285,7 |
715,3 |
24 |
2014 |
56735,9 |
17695,5 |
|
10 |
2000 |
4476,8 |
1365,7 |
25 |
2015 |
58531,1 |
18402,8 |
|
11 |
2001 |
5886,8 |
1963,1 |
26 |
2016 |
61398,5 |
19773,4 |
|
12 |
2002 |
7484,1 |
2169,3 |
27 |
2017 |
65289,5 |
21681,2 |
|
13 |
2003 |
9058,7 |
2755,1 |
28 |
2018 |
70147,5 |
22764,5 |
|
14 |
2004 |
11477,9 |
3558,9 |
29 |
2019 |
75578,5 |
24862,4 |
|
15 |
2005 |
14438,2 |
4338,7 |
30 |
2020 |
75062,8 |
25659,3 |
Данная работа посвящена реализации моделей векторной авторегрессии в бесплатном кросс-платформенном программном пакете Gretl, преимущество которого состоит в русифицированном интерфейсе, что значительно облегчает построение, диагностику и применение эконометрических моделей и способствует внедрению в учебные процессы вузов.
Основная цель данной работы состоит в сравнении возможностей реализации основных этапов построения моделей VAR в Gretl и программной среде R, таких как предварительная обработка данных (проверка данных временных рядов на стационарность, при необходимости, их преобразование); выбор максимальной величины лага, учитываемого в спецификации модели (при помощи обобщенных информационных критериев); оценка параметров VAR-модели, диагностика предпосылок оцененной модели при помощи обобщенных тестов – многомерных аналогов одномерных тестов на автокорреляцию (Portmanteau Test), гетероскедастичность (обобщенные LM-тесты ARCH), нормальность распределения возмущений (Jarque-Bera test).
Для построения модели VAR (для иллюстративной цели) воспользуемся данными макроэкономических показателей (основных компонент ВВП): расходы на конечное потребление (Y) и валовое накопление (X) в РФ. В таблице приводятся годовые данные показателей за период с 1991 по 2020 г. включительно (в млрд руб.) [3].
Предварительная обработка данных. Для проверки временных рядов на стационарность используется расширенный тест Дики – Фуллера: в программной среде R выполняемый при помощи функции adf.test(y) пакета {tseries}, в Gretl данная операция осуществляется из меню «Переменная» главного окна, включающего опцию «Тесты единичного корня», в которой выбирается функция «Расширенный тест Дики – Фуллера (ADF-тест).
В появившемся окне назначаются максимальный порядок лага и три тестируемые модели, используемые в тесте ADF (модели с ограничениями: без константы и тренда, с константой и без тренда; модель без ограничений – с константой и трендом), указывается тип проверяемого на стационарность ряда: уровни переменной, первые разности переменной. Как и следовало ожидать, макроэкономические ряды Y и X нестационарны (по результатам проверки в R и Gretl). Поэтому в качестве первичной обработки они были подвергнуты логарифмированию и вычислению разностей первого порядка. Преобразованные переменные y и x (логарифмические доходности) по результатам ADF-теста являются стационарными и используются в качестве исходных переменных при построении модели VAR.
Выбор параметра авторегрессии. Максимальная величина лага p модели VAR(p) подбирается при помощи информационных критериев – критериев качества моделей, учитывающих компромисс между их точностью и сложностью. Модель оценивается при различном количестве лагов для проверки устойчивости результата к спецификации модели. В моделях векторной авторегрессии, для определения максимальной величины лага, используются обобщенные информационные критерии Акаике, Шварца и Хеннана – Куина, отличающиеся штрафными функциями на количество оцениваемых параметров [4]:
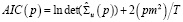 , (1)
, (1)
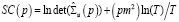 , (2)
, (2)
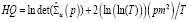 , (3)
, (3)
где m – число переменных VAR-модели, T – объем выборки, 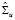 – оценка автоковариационной матрицы вектора возмущений. Вычисление перечисленных статистик и выбор максимального лага модели векторной авторегрессии в программной среде R выполняется при помощи функции VARselect() пакета {vars}:
– оценка автоковариационной матрицы вектора возмущений. Вычисление перечисленных статистик и выбор максимального лага модели векторной авторегрессии в программной среде R выполняется при помощи функции VARselect() пакета {vars}:
varmat <- as.matrix(cbind(y,x))
VARselect (varmat, lag.max = 4, type = «cons»,exogen = NULL)
Вычисление информационных критериев (1)–(3) и выбор максимального лага модели векторной авторегрессии в программной среде Gretl выполняется следующем порядке: в основном окне программы выбирается меню «Модель», далее опция «Временные ряды», «Multivariate» (многомерные), «VAR lag selection» (рис. 1).
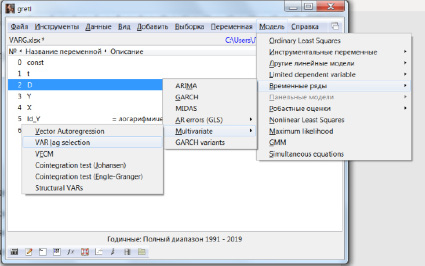
Рис. 1. Определение «оптимального» параметра авторегрессии
Результаты выбора величины лага в R и Gretl совпадают: критерии Акаике и Хеннана – Куина указывают на величину лага – 3, критерий Шварца (налагающий больший штраф на увеличение числа параметров) – 1. Оценим модель векторной авторегрессии третьего порядка:
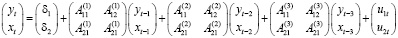 .
.
Оценка параметров модели VAR(p). После уточнения спецификации модели выполняется оценка её параметров. Если случайные возмущения уравнений представляют собой белый шум, для оценки параметров модели VAR применяется обычный метод наименьших квадратов (МНК), который последовательно применяется к каждому уравнению системы отдельно. Для оценки модели VAR(p) и построения прогнозов в программной среде R используется функция VAR () пакета {vars}:
varfit <- VAR(varmat,3,type=”cons”,ic=”AIC”); summary(varfit)
Оценка параметров модели векторной авторегрессии в Gretl выполняется в следующей последовательности: на главной панели выбирается меню «Модель», далее «Временные ряды», «Multivariate» (многомерные), функция «Vector Autoregression» и выбираются переменные, включаемые в спецификацию. Результаты оценивания параметров модели VAR(3), показателей её качества и значимости в R и Gretl совпадают:
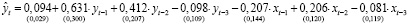
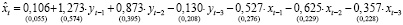
Диагностика VAR(p)-моделей. После оценки параметров VAR-модели выполняется диагностика предпосылок оцененной модели при помощи обобщенных тестов – многомерных аналогов одномерных тестов на автокорреляцию, гетероскедастичность, нормальность распределения возмущений. Для тестирования автокорреляции применяется тест Портманто (Portmanteau Test), являющийся обобщением теста Бокса – Пирса для многомерных временных рядов. Статистика теста [5, 6]:
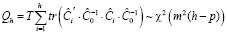 ,
, 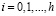
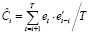 – оценка автоковариационной матрицы вектора остатков модели VAR(p), p – порядок модели векторной авторегрессии, h – порядок автокорреляции, m – число эндогенных переменных модели, используется для проверки нулевой гипотезы:
– оценка автоковариационной матрицы вектора остатков модели VAR(p), p – порядок модели векторной авторегрессии, h – порядок автокорреляции, m – число эндогенных переменных модели, используется для проверки нулевой гипотезы:
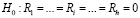 ,
, 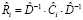 ,
, 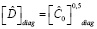 .
.
В программной среде R тест выполняется при помощи функции serial.test пакета {vars}:
serial.test(varfit, lags.pt=6, type=”PT.adjusted”)
data: Residuals of VAR object varfit
Chi-squared = 12.757, df = 12, p-value = 0.3869
В Gretl результаты тестирования включены в протокол оцененной модели: Портманто-тест (Portmanteau): LB(6) =13,778, Ст. свободы = 12 [0,315].
Результаты тестирования показывают отсутствие автокорреляции в остатках модели, небольшое отличие значений статистик в R и Gretl объясняется различием алгоритмов, реализующих их вычисления.
Для исследования гетероскедастичности в многомерных моделях временных рядов используются тесты ARCH, основанные на оценивании вспомогательной модели вида [5]:
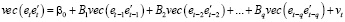 , (4)
, (4)
где 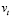 – процесс белого шума,
– процесс белого шума, 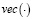 – оператор формирования вектора из нижней треугольной матрицы с элементами на главной диагонали и вертикальным выстраиванием её столбцов. Нулевая и альтернативная гипотезы формулируются следующим образом:
– оператор формирования вектора из нижней треугольной матрицы с элементами на главной диагонали и вертикальным выстраиванием её столбцов. Нулевая и альтернативная гипотезы формулируются следующим образом:
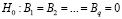 ,
, 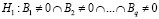 , (5)
, (5)
и проверяются при помощи статистики
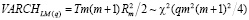 ,
,
где 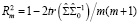 – коэффициент детерминации вспомогательной модели, q – максимальная величина лага, включенная в модель,
– коэффициент детерминации вспомогательной модели, q – максимальная величина лага, включенная в модель, 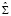 – автоковариационная матрица вектора возмущений модели без ограничений на параметры (4) ,
– автоковариационная матрица вектора возмущений модели без ограничений на параметры (4) , 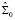 – с ограничениями на параметры в рамках гипотезы
– с ограничениями на параметры в рамках гипотезы 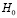 (5). В программной среде R тест выполняется при помощи функции arch.test пакета {vars}:
(5). В программной среде R тест выполняется при помощи функции arch.test пакета {vars}:
arch.test(varfit, lags.multi=3); ARCH (multivariate)
data: Residuals of VAR object varfit
Chi-squared = 40.457, df = 27, p-value = 0.0464,
в Gretl – в меню протокола оцененной модели нужно выбрать: Тесты, тест на наличие ARCH процессов (рис. 2).
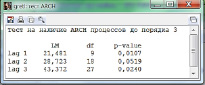
Рис. 2. Результат тестирования гетероскедастичности остатков в Gretl
Результаты тестирования показывают отсутствие гетероскедастичности в остатках модели, небольшое отличие значений статистик в R и Gretl, как и при тестировании автокорреляции, объясняется различием алгоритмов, реализующих их вычисления.
Тестирование предпосылки о нормальном распределении возмущений модели можно выполнить при помощи обобщенного теста Харке – Бера (Jarque-Bera test), статистика которого вычисляется по формуле
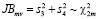 ,
, 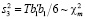 ,
,
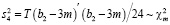 ,
,
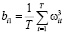 ,
, 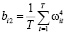 ,
,
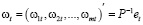 ,
,
где Р – матрица факторизации для ковариационной матрицы вектора остатков 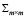 , используемая для нормирования моментов. В программной среде R тест Харке – Бера реализован в функции normality.test пакета {vars}:
, используемая для нормирования моментов. В программной среде R тест Харке – Бера реализован в функции normality.test пакета {vars}:
normality.test(varfit, multivariate.only=TRUE); JB-Test (multivariate) data: Residuals of VAR object varfit Chi-squared = 23.738, df = 4, p-value = 9.015e-04
К настоящему времени разработаны различные модификации теста Харке – Бера, в зависимости от выбора матрицы факторизации. В тесте Дурника – Хансена (Doornik-Hansen) [7], реализованного в Gretl, применяются преобразования матрицы факторизации, позволяющие нормальный случайный вектор свести к стандартному нормальному вектору, что способствует сокращению времени вычислительных процедур. Для тестирования предпосылки о нормальном распределении возмущений VAR-модели в Gretl в меню протокола оцененной модели выбирается: Тесты, Нормальность остатков. Как тест Харке – Бера, так и тест Дурника – Хансена отклоняют нулевую гипотезу о нормальном распределении возмущений модели (рис. 3).
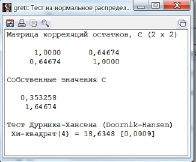
Рис. 3. Тест Дурника – Хансена в Gretl
Функции импульсного отклика. Для обратимого процесса векторной авторегрессии, в случае стационарности всех временных рядов, образующих многомерный вектор эндогенных переменных, векторную модель авторегрессии представляют в форме скользящего среднего (VMA (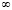 )):
)):
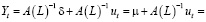
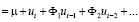 . (6)
. (6)
Оператор
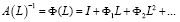 .
.
– передаточная функция фильтра, выражающая совместное влияние на эндогенную переменную остальных переменных. Коэффициентами разложения оператора 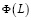 по степеням лагового оператора L являются матрицы
по степеням лагового оператора L являются матрицы 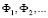 называемые импульсными мультипликаторами. Для периода упреждения s модель (6) принимает вид
называемые импульсными мультипликаторами. Для периода упреждения s модель (6) принимает вид
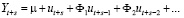 .
.
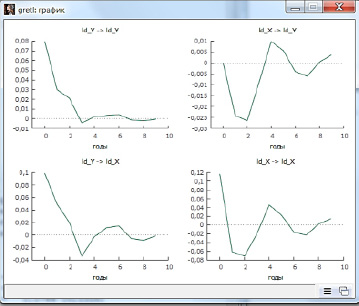
Рис. 4. Графики функций импульсного отклика всех переменных модели
Элементами матрицы 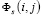 (i – индекс переменной, j – индекс случайного возмущения (шока)) являются производные
(i – индекс переменной, j – индекс случайного возмущения (шока)) являются производные 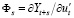 , которые измеряют реакцию переменной Yi в момент t+s на единичное изменение шока в переменной Yj в момент t. Динамика влияния на переменную Yi единичного шока εj в переменной Yj :
, которые измеряют реакцию переменной Yi в момент t+s на единичное изменение шока в переменной Yj в момент t. Динамика влияния на переменную Yi единичного шока εj в переменной Yj :
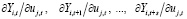 (7)
(7)
называется функцией импульсного отклика (отдачи) (impulse-response function, IRF). Для построения функции импульсного отклика (7) и её графика в R применяются функции
irf.x<-irf(varfit, impuls=”y”, response=”x”, n.ahead=5); plot(irf.x).
В Gretl – на панели результатов оценивания модели VAR(3) выбирается меню «Анализ» и функция «импульсные отклики». Выбираются переменные, для которых строятся функции импульсного отклика и горизонт прогнозирования. Имеется возможность размещения всех графиков на одном рисунке (рис. 4).
Как следует из рис. 4, импульсы (шок) в переменной «накопление» и «потребление» в начальный момент времени оказывают большое влияние на их значения в следующем периоде времени, но эффекты со временем стабилизируются.
Разложение дисперсии ошибки прогноза VAR(p)-модели. Помимо функций импульсного отклика важным инструментом анализа методологии VAR является декомпозиция дисперсий ошибок прогнозов (variance decomposition) [4]. Дисперсия ошибки прогноза определяется как сумма
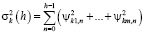
– дисперсия ошибки прогноза k-й переменной с периодом упреждения h, m – число эндогенных переменных в модели VAR(p) в форме векторного скользящего среднего:
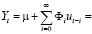
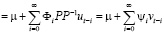 ,
,
где 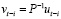 ,
,  . Влияние переменной j на прогнозную дисперсию ошибки переменной k для периода упреждения h обычно представляют в процентном выражении.
. Влияние переменной j на прогнозную дисперсию ошибки переменной k для периода упреждения h обычно представляют в процентном выражении.
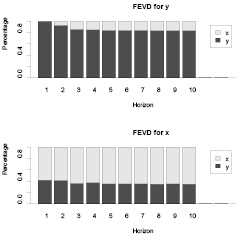
Рис. 5. График декомпозиции дисперсий прогноза переменных модели
Для вычисления составляющей дисперсии ошибок прогноза и их графического представления в программной среде R применяются следующие функции пакета {vars}:
fevd.var<-fevd(varfit, n.ahead=10); fevd.var
plot(fevd.var,addbars=2)
График декомпозиции дисперсий прогноза переменных модели представлен на рис. 5.
Из рис. 5 следует, что 90 % дисперсии переменной «потребление» вызвано самим потреблением, в то время как только около 60 % дисперсии переменной «накопление» вызвано самим накоплением, а остальные 40 – потреблением.
В Gretl – на панели результатов оценивания модели VAR(3) выбирается меню «Анализ» и функция «Прогноз для разложения дисперсии». Для графического представления прогноза разложения дисперсии, на панели результатов оценивания модели VAR выбирается меню «Графики» и в функции «прогноз для разложения дисперсии» выбирается горизонт прогнозирования, вид гистограммы, переменная, для которой строится гистограмма прогнозов разложения дисперсии для заданного горизонта прогнозирования.
Оценивание моделей векторной авторегрессии в кросс-платформенном программном пакете Gretl и программной среде R показало идентичность реализованного в них инструментария для построения, диагностики и исследования моделей. Выбор пользователей определяется их предпочтениями: оба продукта являются бесплатными и свободно распространяемыми. Однако следует отметить такие преимущества Gretl, как русифицированный интерфейс, простоту использования, возможность применения без знания языков программирования. Это способствует внедрению Gretl в учебные процессы вузов в блоке эконометрических дисциплин.



