В модельных задачах с высокой размерностью в процессе решения с целью построения матриц, размеры которых достигали до 1000, разрабатываются генераторы матриц. Поэтому необходимо для решения подобных задач разработать программные продукты. Известно, что в процессе построения балансовых моделей, погрешности исходных данных модели приводят как к небольшим погрешностям, так и к большим погрешностям результатов решения.
Известно, что при применении модели для решения практических задач ее исходные данные могут быть заданы неточно. Известно, что если небольшие ошибки исходных данных незначительно влияют на результат решения модели, то в этом случае модель называется корректно поставленной, а если значительно влияют на результат решения, то в этом случае модель называется некорректно поставленной.
В случае, когда исходные данные, допускающие некоторые неточности, приводят к незначительным погрешностям результатов ее решения, то для решения задач можно применить итерационные методы. А в случае, когда исходные данные, допускающие некоторые неточности, приводят к значительным погрешностям результатов ее решения, можно применить метод регуляризации.
Цель исследования – разработать методики неотрицательного решения двойственной балансовой модели с учетом её обусловленности, реализовать в программу разработанную методику, разработать модель межотраслевого баланса ЗАО «Фотон» и найти его неотрицательное решение с помощью разработанной программы.
Материалы и методы исследования
Для получения результатов исследования были использованы метод итерации и метод регуляризации. Применены усредненные статистические данные за 2018–2021 гг. ЗАО «Фотон».
Результаты исследования и их обсуждение
Рассмотрим балансовую модель вида [1–3]:
x = Ax + f (1)
Здесь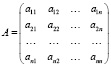 
является технологической матрицей размерности n×n, которая обладает неотрицательными элементами.
Известно, что модель, двойственная к модели (1), имеет вид
p = ATp + v, (2)
где p является вектором цен производимой отраслями продукции, v является вектором добавленной стоимости,
является матрицей транспонированной к матрице A модели (1).
Известно, что в случае прибыльности модели (2) модель (1) является продуктивной и, наоборот, в случае продуктивности модели (1) модель (2) является прибыльной.
Далее представим модель (2) в виде
(I – AT)p = v. (3)
Обозначим (I – AT) = D, тогда модель (3) будет иметь вид
Dp = v. (4)
Является ли решение (4) устойчивым, зависит от незначительных погрешностей исходных данных (4) и погрешности, которая появляется при большой размерности n, приводящей к незначительным погрешностям полученного решения.
Обозначим через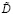 
и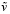 
отличные от точных значений величины (4), тогда модель имеет вид
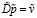. (5)
Относительно моделей (4) и (5) получим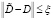 
, 
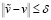, где ξ является погрешностью 
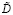, δ является погрешностью вектора 
.
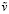Тогда относительную погрешность решения (5) можно представить в виде
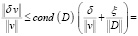
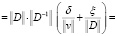
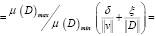
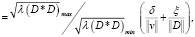
где cond(D) является числом обусловленности D; μ(D) является сингулярным числом; λ является собственным числом.
Решение модели (4) является устойчивым в зависимости от числа обусловленности матрицы. Например, в случае condAT ≤ 1000 решение (4) является устойчивым, а в случае condAT > 1000 решение (4) является неустойчивым.
При первом случае для неотрицательного решения рассматриваемой модели применяем итерационный метод. В таком методе точность результата подсчета в каждой итерации определяется лишь результатом предшествующей итерации, практически не зависящем от предыдущих подсчетов [4, c. 136]:
pk+1 = ATpk + v, p0 = θ, k = 0, 1, 2,… (6)
Известно, что матрица AT из (4) является прибыльной, если ||AT|| < 1.
Если ||AT|| < 1 истинно, то решение (2):
1) существует и оно единственное;
2) при ∀p0 процесс (6) сходится и справедливой является следующая оценка:
||pk – p|| ≤ ||AT|| ||p0 – p||, (7)
где p является решением (2).
В системе (6) нет ограничения p ≥ 0.
Если элементы AT, v имеют некоторые погрешности, то иногда можно получить решение p, к большим погрешностям и для этого случая надо применить метод регуляризации.
Предположим, что (4) некорректно поставлена и
, 
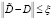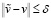. (8)
Будем искать приближенное решение (5), применяя метод регуляризации [5, 6].
Из [5, 7] известно, что нахождение решения (4) на основе (5) сводится к поиску pα, минимизирующего сглаживающий функционал:
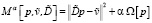, α > 0, (9)
где Ω[p] = ||p||2 называется стабилизирующим функционалом, α = α(δ) – параметром регуляризации.
Из [5, 7] известно о существовании одного pα, которое можно определить при любом фиксированном α > 0 из
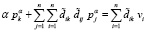, (10)
.
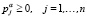Опишем следующий алгоритм:
1. Вводим значение n.
2. Вводим значения элементов AT.
3. Вводим значения элементов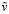 
.
4. Задаём начальное приближение p0.
5. Задаём погрешность ε > 0, для вычисления p.
6. Вычисляем condAT.
7. Если condAT ≤ 1000, то переходим к пункту 8, иначе переходим к шагу 11.
8. Проверяется выполнимость условия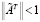 
.
9. Если условия пунктов 7, 8 выполнимы, то для вычисления применяем формулу (4) до достижения необходимой погрешности ε > 0.
10. В случае невыполнимости условия из пункта 8 вычисляем другую норму 
.
11. Задаем α1 > 0.
12. При α1, находим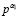 
из (10).
13. При известных α1,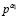 
, вычисляем 
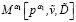из (9).
14. Задаем α2 > 0, α2 < α1.
15. При α2, находим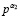 
из (10).
16. При известных α2,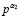 
, вычисляем 
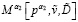из (9).
17. Если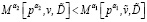 
, то переходим к шагу 19.
18. Если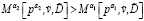 
, то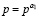 
.
19. Задаем α3 > 0, α3 < α2.
20. При α3, находим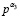 
из (10).
21. При α3,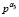 
, вычисляем 
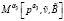из (9).
22. Если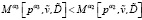 
, то переходим к шагу 24.
23. Если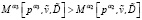 
, то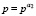 
.
24. Задаем α4 > 0, α4 < α3.
25. Таким образом, продолжается до тех пор, пока на (k+1)-м шаге не отыщутся αk+1,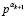 
, при которых
,
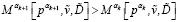то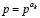 
и процесс завершается.
Описанный алгоритм был реализован в программный продукт на языке программирования С ++.
В таблице представлена принципиальная схема межотраслевого баланса ЗАО «Фотон», для построения которой были применены усредненные статистические данные ЗАО «Фотон» за 2018–2021 гг.
Принципиальная схема межотраслевого баланса ЗАО «Фотон» за 2018–2021 гг.
|
Производящие отрасли |
Потребляющие отрасли (тыс. руб.) |
Конечный спрос (тыс. руб.) |
Валовой продукт (тыс. руб.) |
|||
|
1 |
2 |
3 |
4 |
|||
|
Производство и распределение электроэнергии |
0 |
4551,1 |
0 |
0 |
19047,3 |
23598.4 |
|
Производство хлебобулочных изделий |
1015,6 |
1663,2 |
0 |
0 |
8331,8 |
11010.6 |
|
Строительство жилых и нежилых зданий |
2131,4 |
0 |
9134,6 |
0 |
17279,6 |
28545.6 |
|
Гостиничный комплекс |
354,6 |
0 |
0 |
2190,4 |
11143,9 |
13688.8 |
|
Амортизация Оплата труда Чистый доход |
20096,8 |
4796,3 |
19411,01 |
11498,5 |
||
|
Валовой продукт |
23598.4 |
11010.6 |
28545.6 |
13688.8 |
||
Из таблицы видно, что:
− отрасль по производству «Производство и распределение электроэнергии» в среднем производит валовую продукцию на сумму 23598,4 тыс. руб.;
− отрасль по производству «Производство хлебобулочных изделий» в среднем производит валовую продукцию на сумму 11010,6 тыс. руб.;
− отрасль по производству «Строительство жилых и нежилых зданий» в среднем производит валовую продукцию на сумму 28545,6 тыс. руб.;
− отрасль по производству «Гостиничный комплекс» в среднем производит валовую продукцию на сумму 13688,8 тыс. руб.
Из таблицы получим:
,
.
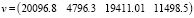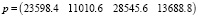Если ЗАО «Фотон» в 2023 г. увеличит значение вектора v на 17 % относительно усредненных данных, т.е.
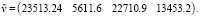
Вводим исходные данные в программу и получим, что матрица хорошо обусловлена condAT ≤ 1000 и
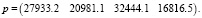
Таким образом,
− отрасль по производству «Производство и распределение электроэнергии» в 2023 г. должна произвести валовую продукцию на сумму 27933,2 тыс. руб.;
− отрасль по производству «Производство хлебобулочных изделий» в 2023 г. должна произвести валовую продукцию на сумму 20981,1 тыс. руб.;
− отрасль по производству «Строительство жилых и нежилых зданий» в 2023 г. должна произвести валовую продукцию на сумму 32444,1 тыс. руб.;
− отрасль по производству «Гостиничный комплекс» в 2023 г. должна произвести валовую продукцию на сумму 16816,5 тыс. руб.
Заключение
Результаты решения показывают, что матрица двойственной модели ЗАО «Фотон» имеет хорошую обусловленность. Она является прибыльной и продуктивной.
Результаты исследования могут представлять интерес для хозяйствующих субъектов при решении их балансовых моделей любой обусловленности.