Может ли самообучающийся агент взять на себя роль трейдера? Может ли обучение с подкреплением эффективно торговать, чтобы заменить реального человека? Может ли искусственный интеллект успешно торговать и выходить в плюс? Данная тематика важна и актуальна в нынешних условиях, поскольку цель любого участника рынка – это как минимум не выйти в минус, а в идеале – выйти в плюс. К сожалению, новички – участники фондового рынка очень часто думают, что торговать – это очень просто [1]. В реальности же трейдеры используют для подобного огромный пласт знаний: знания текущего состояния рынка, используют технические индикаторы, парсят и исследуют различные новостные ресурсы – это титанический труд, который может быть сведен к математике, теории вероятностей и математической статистике.
Алгоритмическая торговля и автоматизированная торговля на фондовом рынке широко исследуется с 1990-х гг. [1]. При торговле целью инвестора является максимизация своего вознаграждения, которая попросту называется прибылью (либо PnL: нереализованная прибыль и убытки). Трейдинг обычно состоит из двух основных действий:
1. Анализ актуального состояния рынка.
2. Принятие определенных действий и решений, которые приводят к увеличению (или, по крайней мере, не уменьшению) прибыли.
История машинного обучения в экономической сфере начинается с различных макроэкономических моделей, в которых исследователи пытались прогнозировать рыночные цены акций [2, 3]. Однако эти исследования обычно терпели неудачу при попытке предсказать цены в краткосрочной перспективе. С развитием математического аппарата (методов глубокого обучения и обучения с подкреплением) данные проблемы удалось решить. К примеру, достаточно популярный метод Q-learning был использован для трейдинга: RL справился лучше, чем методы обучения с учителем. Это было одно из самых первых исследований в данной области [4].
Методы технического анализа также были широко исследованы для прогнозирования рынка. Трейдеры часто анализируют технические индикаторы рынка, потому что они показывают прогностическую способность и способны сообщать о различных паттернах на рынке [5].
Существует достаточно много статей, посвященных использованию нейронных сетей в трейдинге. К примеру, в статье использовалась сверточная нейронная сеть, в качестве аппроксимации Q-функции [6]. Были и попытки внедрения других технологий обучения с подкреплением в алгоритмической торговле, таких как Deep Q-Network (DQN), Duel Doble DQN и др.
Технология Deep Q-Network (DQN) широко протестирована на видеоиграх и прикладных технических задачах, например, при решении охлаждении серверов (https://tproger.ru/news/google-deepmind-cooling/). Однако только относительно недавно начались активные исследования в области торговли. Многие роботы уже добились успехов. Однако данная технология в алгоритмической торговле широкого применения пока не получила. Известно, что DQN переоценивает значения действий из-за шума и неточной аппроксимации функций. Для решения этой проблемы был реализовали алгоритм Double DQN [7].
В работе [8] описана технология глубокого обучения с подкреплением Dueling Double DQN. Авторами доказано, что данный алгоритм улучшает качество обучения и производительность в целом всей системы. Но для волатильных акций не исследовалось, как ведет себя данная технология, когда рынок непредсказуем (локдауны, кризисы и т.д.).
Из приведенных источников видно, что технологии обучения с подкреплением внедряются в алгоритмическую торговлю. Следовательно, данное исследование является актуальным.
Целью исследования является разработка различных алгоритмов глубокого обучения с подкреплением (DQN, DDQN, DDDQN) для алгоритмической торговли и ее тестирование на российских акциях в различных условиях.
Материалы и методы исследования
Построение торговой среды. Сначала мы вводим биржевые данные Open-High-Low-Close-Volume-OpenInt в торговую среду через загрузчик данных. Часть этих данных используется на этапе обучения, когда агент узнает, какое действие предпринять, основываясь на вознаграждении, которое он получает, агент взаимодействует с окружающей средой, предпринимая какие-либо действия. Затем производится тест на данных вне выборки.
В созданной торговой среде агент может решать, когда открывать длинные или короткие позиции по одной акции. У агента также есть свобода принятия решения: он может в любой момент продать, купить или удерживать акцию, когда он захочет, за исключением того, что он может занимать только одну позицию одновременно. Например, если у него есть длинная позиция, он не может одновременно иметь короткую позицию. Ему нужно закрыть свою длинную позицию, а затем открыть короткую. Кроме того, было добавлено состояние флэт, где агент может просто наблюдать за рынком, не имея длинной или короткой позиции. В таком случае агент просто удерживает акцию и наблюдает за состоянием рынка.
Чтобы стабилизировать процесс обучения и обучить нейронную сеть дополнительной информации в период обучения, был внедрен модуль памяти. Для выполнения воспроизведения опыта агент во время обучения сохраняется на каждом временном шаге в памяти агента. При каждом обновлении весов нейронной сети обновления Q-значений применяются к случайно выбранной выборке этих опытов.
Рассмотрим состояния агента.
Самое очевидное это
[price(t–1), price(t), positionprice, position],
где t – это время, positionprice – цена, по которой агент вошел в позицию (позиция: короткая, длинная, флэт).
Однако на основе опыта других исследователей, а также первых версий работы был сделан вывод, что агент не мог узнать много информации всего из предыдущей и нынешней цены. Когда трейдер в реальности смотрит на график цен, он смотрит по цене 100–1000 пунктов перед открытием позиции, поэтому было принято решение дать агенту возможность смотреть в историю индекса. В противном случае агент лишь удерживал актив и крайне редко предпринимал какие-либо действия.
Действия, которые может предпринимать агент – это купить актив, продать или удержать.
Награда – это максимизация вознаграждения (выбирая ту или иную позицию).
Построение моделей
1. Deep Q-сеть (DQN)
Определим функцию Q (s, a) так, чтобы для данного состояния s и действие a оно возвращало оценку общей награды, которой можно достичь, если мы начнем с этого состояния. Q-Learning использует понятие уравнение Беллмана, агент DQN выбирает действие в соответствии с жадной политикой, максимизация функции Q *.
Q*(st, a) → r(st, at) + γmaxαQ*(st+1, a);
Q* – оптимальное Q значение;
γ – коэффициент дисконтирования;
s – state, a – action, r – reward.
Это уравнение сходится к желаемому Q* при условии, что существует конечное число состояний, и каждая пара состояние-действие представлена неоднократно. Чаще всего, Q-функция в реальности не обладает таким свойством, поэтому стараются найти различные ее аппроксимации, к примеру, с помощью нейронных сетей: Deep Q-Сеть (DQN). Однако использование нейронной сети все равно является не идеальным вариантом, потому что она склонна к переоцениванию действий и зашумлению [8]. Именно по этой причине был введен блок памяти агента, чтобы стабилизировать обучение. Данный модуль должен заставлять нашу модель лучше сходиться.
На рис. 1 представлена архитектура модели DQN.
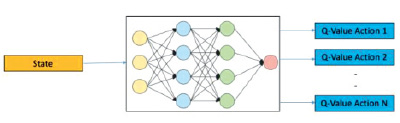
Рис. 1. Архитектура модели DQN
2. Double-DQN
Одна из проблем, с которыми сталкивается агент DQN, заключается в том, что агент имеет тенденцию переоценивать функцию Q из-за максимума в формуле и, таким образом, плохо сходится. При оценке функции Q для определенного состояния оценка зашумлена и отличается от истинного значения, всё это распространяется на другие состояния. Чтобы решить эту проблему, был создан алгоритм Double DQN (DDQN). В DDQN существуют две отдельные функции Q. Одна сеть используется для определения максимального действия, в то время как другая сеть оценивает стоимость (рис. 2).
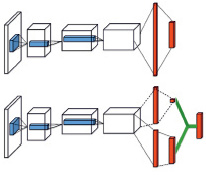
Рис. 2. Архитектура модели Double-DQN
Убирая максимизирующие действия из его значения, мы можем исключить предвзятость максимизации. Изменение оценки выглядит следующим образом:
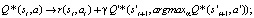
Q* – оптимальное Q значение;
γ – коэффициент дисконтирования;
s – state, a – action, r – reward, Q', s', a' – это целевые значения Q – cети.
Это помогает повысить стабильность процесса обучения. Данный алгоритм уже зарекомендовал себя в решении сложных задач [7].
3. Dueling Double DQN
Существует также еще более производительный алгоритм: Dueling Double DQN (DDDQN). С математической точки зрения данный алгоритм выглядит следующим образом:
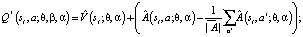
Q* – оптимальное Q значение;
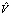– значение первой сети; β – параметр сети;
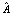– Dueling сеть (Advantage); α – параметр этой сети;
s – state, a – action, r – reward, Q', s', a' – это целевые значения Q – cети.
В данном алгоритме благодаря разделению так называемых потоков агент лучше дифференцирует действия друг от друга. Это значительно улучшает обучение. Кроме того, в DQN на каждой итерации для каждого состояния в пакете мы обновляем только Q-значения за действия, предпринятые в состоянии. Это приводит к более медленному обучению в случае действий, которые были редко использованы и не выучены в блоке.
Результаты исследования и их обсуждение
Рассмотрим работу всех трех моделей на одном наборе данных.
В качестве данных агент обучается торговле акциями компании Яндекс (YNDX) c января 2018 г. по июнь 2021 г., где цены акции, лежащие в пределах от конца 2019 г. до нынешнего времени, – это тестовый набор данных. Отметим, что данный период для теста особенно интересен в связи с обширными финансовыми новостями и вспыхнувшей пандемии вируса SARS-CoV-2. Такие новости приводят к непредвиденным колебаниям на рынке, что еще больше подогревает интерес к поведению агента [9].
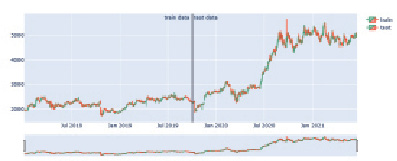
Рис. 3. Динамика актива
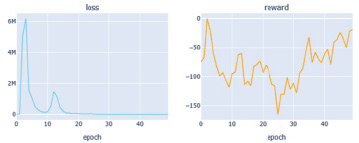
Рис. 4. Графики потерь и наград агента DQN
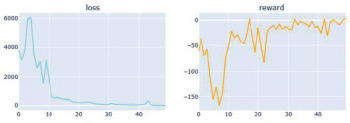
Рис. 5. Графики потерь и наград агента DDQN
На рис. 3 представлена динамика данного актива.
Можно заметить, что в начале 2020 г. актив вел себя странно (из-за ситуации с ковидом и локдауном), с июля 2020 г., то наблюдается активный рост (видимо, в связи с планированием Яндекса покупки банка Тинькофф и снятие локдауна), а после известии об отмене покупки, акции рухнули вниз.
На рис. 4–6 приведены графики обучения агентов для трех моделей.
Сравнивая наши графики, мы видим, что все три агента показывают неплохие результаты (потери сходятся, а награда c эпохой увеличивается). Из всех лучшие результаты с точки зрения потерь, а также вознаграждения имеет агент Dueling Double DQN. Мы также можем заметить, что потери в DQN не совсем стабильны, и это связано с положительной систематической переоценкой, однако на тестовой выборке данная модель показала второй результат.
Далее все модели были протестированы на 50 % наборе тестовых данных. На тестовом прогоне агент DDDQN имеет наибольший доход (рис. 7).
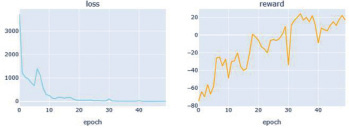
Рис. 6. Графики потерь и наград агента DDDQN
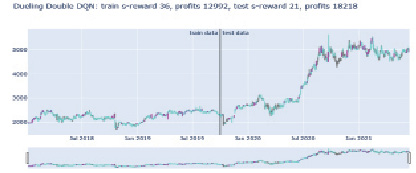
Рис. 7. Тест агента DDDQN
Заключение
В данной работе были продемонстрированы три алгоритма обучения с подкреплением, а также показано, что стратегии обучения с подкреплением могут успешно торговать на финансовом рынке и выходить в плюс. Обучение с подкреплением кардинально отличается от supervised learning и от типичного экономического подхода тем, что в последних прогнозам необходимо пройти через модели риска и исполнения, тогда как в обучении с подкреплением мы можем торговать с ограничениями в структуре вознаграждений. Лучшей моделью оказалась DDDQN.