Приведем классическое определение нечетких множеств.
Определение. Нечетким множеством А называется множество упорядоченных пар вида
<x, μA(x)>,
где x является элементом некоторого универсального множества X, а μA(x) – функция принадлежности μA(x): X → [0; 1].
В работе [1] один из авторов показал, что нечеткие множества вкладываются в пространство банаховых сеток или банаховых матриц.
Цель исследования заключается в рассмотрении некоторых примеров использования нечетких множеств, в том числе в геометрии пространств Банаха и экономике.
Материалы и методы исследования
Элементы нечеткой геометрии пространств Банаха
С теорией линейных нормированных пространств можно ознакомиться в оригинальном переиздании книги С. Банаха (на русском языке см. [2]).
Известно, что H-свойством обладает каждое локально равномерно выпуклое (LUR) банахово пространство. Напомним соответствующее определение:
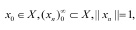
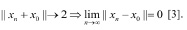
Пусть X – банахово пространство и x,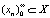 
. Известно, что последовательность xn слабо сходится к элементу x, если 
.
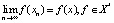Определение. Банахово пространство Х называется слабо локально равномерно выпуклым (обозначается Х∈WLUR), если из условий
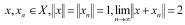
следует слабая сходимость последовательности xn к элементу x [4].
Определение. Сопряженное банахово пространство Х* называется слабо* локально равномерно выпуклым (обозначается Х*∈W*LUR), если из условий
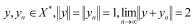
следует слабая* сходимость последовательности yn к элементу y [3].
Введем понятие нечеткой слабой локальной равномерной выпуклости, которая есть обобщение слабой и * – слабой локальной равномерной выпуклости пространств Банаха.
Определим нечеткую слабую сходи- мость.
Пусть X – банахово пространство и x,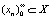 
. Последовательность xn нечетко слабо сходится к элементу x, если 
.
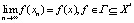Определение. Пространство X называется нечетко слабо локально равномерно выпуклым, если из условия
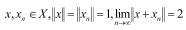
следует нечеткая слабая сходимость последовательности xn к элементу x, т.е.
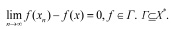
Очевидно, если X нечетко слабо локально равномерно выпукло при Г = Х*, то получим обычное WLUR – свойство пространства Х. Если Х* нечетко слабо локально равномерно выпукло при Г = Х, то получим Х*∈W*LUR. Очевидно, что если Г ⊃ Г1, то из Х нечетко слабо локально равномерно выпукло при Г следует, что Х нечетко слабо локально равномерно выпукло при Г1.
В случае сепарабельных пространств Г вопрос о наличии эквивалентной нормы, относительно которой Х нечетко слабо локально равномерно выпукло, решается следующим утверждением, которое представляет собой аналог теоремы Кадеца [4] и которое в другой формулировке доказано в работе [5].
Теорема 1. Любое банахово пространство X обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме для всех Г – сепарабельных подпространств Х*.
Пусть Т – произвольное множество. Тогда через ℓ∞ (Т) обозначают банахово пространство всех ограниченных вещественных функций на Т с нормой
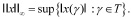
Когда Т = N – множество целых положительных чисел, просто пишут ℓ∞.
Известно, что несепарабельное банахово пространство l∞ не становится локально равномерно выпуклым ни в какой эквивалентной норме, тем не менее отсутствие локальной равномерной выпуклости ни в какой эквивалентной норме не отменяет нечеткой слабой локальной равномерной выпуклости в эквивалентной норме. Из теоремы 1 получаем
СЛЕДСТВИЕ 1.1. Пространство l∞ обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме для всех Г – сепарабельных подпространств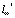 
.
Более того, так как l1 – сепарабельное пространство,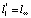 
, из теоремы 1 получаем для l∞ «вполне четкое» свойство слабой* локальной равномерной выпуклости.
СЛЕДСТВИЕ 1.2 [5]. Пространство l∞ допускает двойственную эквивалентную слабо* локально равномерно выпуклую норму.
Среди банаховых пространств одним из наиболее исследованных является класс слабо компактно порожденных банаховых пространств (обозначается X∈WCG). Известно, если X – сепарабельное пространство, то X – слабо компактно порожденное пространство.
Возникает вопрос: в каких случаях банахово пространство X обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме, если Г – несепарабельное пространство? В этом направлении можно доказать следующие утверждения, которые в другой формулировке доказаны в работе [6].
Теорема 2. Пусть X*∈WCG (или X∈WCG). Тогда банахово пространство X обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме для всех Г-подпространств Х*.
Теорема 3. Пусть X∈WCG. Тогда банахово пространство X* обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме для всех Г-подпространств Х.
Экономические приложения теории нечетких множеств
К банаховым пространствам относится векторное пространство, имеющее широкие приложения в экономике. В экономической практике приходится оперировать действительными числами, отражающими прогнозные значения, например, отдельных элементов денежного потока при оценке инвестиционных проектов, экспертные оценки ожидаемого уровня инфляции, цен на сырьевые товары, доходов и т.п. Учитывая, что подобные оценки, как правило, не являются точными, в экономике все в большей степени используются нечеткие числа, нечеткие множества и нечеткая логика.
Волкова Е.С. и Гисин В.Б. выделили четыре укрупненных класса нечетких моделей на основе природы возникновения неопределенности [7]: модели, использующие нечеткие числовые величины (например, в задаче внутренней нормы доходности денежного потока в случае нечетко определенных платежей); модели нечеткого управления на основе лингвистических переменных с использованием определенного количества правил вывода (используются в условиях высокой неопределенности, когда приходится учитывать плохо формализуемые факторы или основываться только на экспертных оценках, например при исследовании влияния норматива достаточности капитала на отношение «банковские активы/ВВП»); оптимизационные модели (например, в задаче нечеткого линейного программирования нечеткими могут являться параметры модели или ограничения), логические модели, использующие нелинейные логические шкалы (например, при оценке аудиторских свидетельств).
В исследовании Лебедевой М.Е. [8] находит подтверждение тезис, что методы теории нечетких множеств используются во всех основных типах моделирования экономических систем: эконометрическом моделировании; моделях общего экономического равновесия; имитационных моделях; балансовых моделях. При анализе и принятии решений в ситуациях с высокой степенью неопределенности прибегают к когнитивному моделированию на основе интеллектуальных карт как способа представления мыслей человека-эксперта. В настоящее время после работ Б. Коско когнитивное моделирование осуществляется на основе нечетких когнитивных карт. Как правило, в экономике к слабо определенным ситуациям относятся макроэкономические процессы. Рассмотренные Лебедевой М.Е. примеры приложения нечетких когнитивных исследований макропроцессов в экономике России, осуществляемые разными исследователями, подтверждают перспективность использования теории нечетких множеств в экономике [8].
Результаты исследования и их обсуждение
Теория нечетких множеств позволяет решать тот же класс задач, который традиционно решается в экономических приложениях. Однако вследствие того, что аппарат теории нечетких множеств оперирует с понятиями, выражаемыми на естественном языке, то получаемые результаты часто оказываются более понятными, легко интерпретируемыми и эффективными, чем при использовании традиционных моделей с высокой степенью абстракции.
Обоснованию применения нечеткой логики к задачам оценки эффективности инвестиционных проектов посвящена, например, работа Тютюкиной Е.Б., Гисина В.Б. [9]. На первом этапе экспертам предлагается оценивать показатели инвестиционного проекта в трех термах («низкое значение», «среднее значение», «высокое значение»). Затем на основе модели нечеткого вывода делается заключение о целесообразности участия инвестора в проекте. При этом мнение экспертов учитывается более полно.
Оценочные суждения на основе методов теории нечетких множеств и нечеткой логики применительно к кредитному скорингу рассмотрены в [10]. Проведенное исследование выявило, что использование в кредитном скоринге нейронных сетей и генетических алгоритмов связано с определенными трудностями интерпретации полученных результатов, в то время как комбинирование указанных методов с методами нечеткой логики допускает более естественное описание результатов вычислений.
Наибольший эффект от применения методов теории нечетких множеств наблюдается при анализе фондового рынка. Например, в работе [11] на основе данных 250 международных компаний построена нечеткая параболическая регрессия отношения «цена – доход», дающая, с одной стороны, инвесторам информацию о компаниях, которые являются недооцененными, и заработать на них определенный доход, а с другой стороны, возможность трансформации прогноза для рынка по фактору «цена – доход» в прогноз капитализации определенной компании.
Жданова О.А., Курагина А.Ю. провели сравнительный анализ традиционной вероятностной модели формирования портфеля ценных бумаг и модели на основе теории нечетких множеств [12]. Нечеткая модель оказалась более информативной применительно к критерию «доходность – риск», а также выявила его существенный рост (то есть снижение риска) при увеличении количества ценных бумаг в портфеле, что согласуется с общепринятой практикой.
Как известно, хорошо разработанный аппарат задач линейного программирования в некоторой степени ограничивал их применение вследствие изменчивости параметров и ограничений модели реальных экономических ситуаций. С использованием методов теории нечетких множеств и нечеткой логики эта проблема преодолевается. Например, в работе [13] исследуется задача оптимизации инвестиционного процесса как задача нечеткого линейного программирования, что позволяет найти оптимальное решение и в условиях неопределенности параметров.
Козловский А.Н. с соавторами показал, что нечетко-логические описания, используемые для моделирования новых нетрадиционных механизмов обеспечения устойчивости предприятий, позволяют повысить эффективность их применения [14]. Внешние воздействия на организацию рассматриваются как нечеткий сигнал, который распространяется по системе организации. Соответственно, последствия также моделируются как нечеткие переменные, а для моделирования ответных мер в виде проектных инициатив используется нечетко-логическое моделирование.
Имеются определенные достижения в применении методов теории множеств к разработкам систем мотивации персонала. Например, Недосекин А.О. с соавторами представил нечеткую модель системы мотивации персонала горнодобывающего предприятия [15]. Проблема заключается в том, что работники более мотивированы на повышение производительности труда, что отражается на их заработке, чем на соблюдение требований в сфере охраны труда и промышленной безопасности. Формирование модели сбалансированных показателей с нечеткими факторами и мягкими связями, а также выявление нечетких калибровочных соотношений позволяет выстроить систему «заработок – штраф» таким образом, чтобы работники были мотивированы как на рост производительности труда, так и на соблюдение требований безопасности.
Заключение
Имеющиеся многочисленные положительные примеры использования методов теории нечетких множеств и нечеткой логики применительно к экономическим приложениям требуют теоретического обоснования и применительно к их базовому пространству – пространству Банаха. Проведенное исследование показало возможность введения понятия нечеткой слабой локальной равномерной выпуклости, определения нечеткой слабой сходимости. Доказано, что любое банахово пространство обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме для всех его сепарабельных подпространств, а также установлены случаи, когда банахово пространство обладает свойством нечеткой слабой локальной равномерной выпуклости в эквивалентной норме для несепарабельных пространств.
Изучение применений теории нечетких множеств и нечеткой логики к задачам, традиционно используемым в экономике, таким как задача линейного программирования, регрессионные модели, модели множественного выбора и другие, показало, что положительные результаты применения связаны со следующими причинами:
– возможностью формулирования задачи на естественном языке, что позволяет учитывать экспертные оценки более полно и повышает содержательную интерпретацию результатов;
– более слабые допущения (нечеткие числа) позволяют получить необходимую информацию для принятия решений в результате оптимизации или моделирования, в том числе и тех в случаях, где жесткие ограничения не приводили к искомому результату.