Рост доходов населения России является важной составляющей ее государственной политики. Так, в соответствии с прогнозами социально-экономического развития Российской Федерации (далее РФ) на период до 2036 г., которые предоставило Министерство экономического развития РФ, за период с 2020 по 2036 гг. планируется достигнуть роста реальной заработной платы в 1,6 раза [1].
Официальная статистика по нашей стране, представленная на сайте Федеральной службы государственной статистики [2], представляет показатель реальных денежных доходов по регионам в динамике, т.е. в процентах к соответствующему периоду предыдущего года, что неудобно при проведении статистического анализа и моделирования. Показатель же средней номинальной начисленной заработной платы по всем регионам представляется в денежном выражении, что обусловливает удобство его использования при проведении статистического анализа данных.
Показатель средней номинальной начисленной заработной платы будет использован в работе в качестве эндогенной переменной, определяющей различия в уровне жизни и благосостояния населения различных регионов России. С помощью этого и других показателей мы увидим диспропорции социально-экономического развития регионов, входящих в один и тот же федеральный округ, и обнаружим «похожесть» в этом смысле регионов, расположенных в территориально различных частях страны. Возможность адекватной оценки уровня заработной платы в регионе является актуальной задачей и позволит региональным властям и работодателям сделать вывод о необходимости индексации заработной платы, если она оказалась ниже требуемого уровня.
Целью исследования являются анализ и прогнозирование уровня среднемесячной номинальной заработной платы на всей территории РФ с учетом региональных дифференциаций.
Для достижения цели были решены следующие задачи:
1) выбраны наиболее информативные факторы из большого перечня социально-экономических показателей, так или иначе связанных с показателем средней номинальной заработной платы;
2) выполнена кластеризация полного перечня регионов РФ по нескольким показателям одновременно для получения информации о группах регионов, схожих по уровню социально-экономического развития, в том числе по уровню доходов;
3) построена эконометрическая модель с фиктивными переменными для оценки различий в уровне доходов населения регионов из разных кластеров;
4) определен перечень регионов, средний фактический уровень номинальной заработной платы в которых не соответствует полученным в ходе исследования нижним и верхним границам;
5) получены прогнозные оценки значений средней номинальной заработной платы при заданном уровне включенных в модель факторов.
Материалы и методы исследования
В работе использовались данные за IV квартал 2019 г., полученные на сайте Федеральной службы государственной статистики [2]. Выбор периода обусловлен тем, что ситуация с пандемией в 2020 г. не позволила бы объективно оценить ситуацию с уровнем доходов населения.
Работа выполнена с использованием методов кластерного анализа, квантильной и классической регрессии. Представленные результаты получены с помощью программ MS Excel, Gretl, R.
Результаты исследования и их обсуждение
На начальном этапе исследования решалась задача выбора информативных факторов, тесно связанных с показателем средней начисленной номинальной заработной платы и значимо влияющих на него (NZP).
В результате корреляционного анализа данных и пошагового отбора статистически значимых факторов для моделирования уровня средней номинальной заработной платы были отобраны два фактора, удовлетворяющие всем необходимым условиям выбора:
1) стоимость фиксированного набора товаров и услуг (FIX), в рублях;
2) инвестиции в основной капитал (IOK), в млн рублей.
Показатель стоимости фиксированного набора потребительских товаров и услуг предназначен для межрегиональных сопоставлений покупательной способности населения по отдельным субъектам РФ. При расчете стоимости минимального набора продуктов питания по РФ и субъектам РФ используются единые (установленные в целом по РФ) минимальные объемы потребления [3]. Объем инвестиций в основной капитал выбран как фактор, влияющий на уровень заработной платы в регионе.
Общий объем исследуемых нами данных включал в себя 82 региона России. Нетрудно сделать вывод о нецелесообразности моделирования номинальной заработной платы на основе сплошной таблицы, включающей все регионы. В силу этого было принято решение провести предварительную кластеризацию регионов по нескольким признакам одновременно. Следует отметить, что, кроме эндогенной переменной и двух выбранных для ее анализа факторов, при кластеризации использовались показатели динамики реальных денежных доходов (RDD) и среднедушевые денежные доходы населения (CDD). Это было сделано для того, чтобы группировка регионов в полученных кластерах в большей степени была обусловлена различиями в уровне доходов населения.
В результате кластеризации мы получили пять кластеров различного объема (табл. 1).
Таблица 1
Результат кластеризации
|
Регион |
Кластер |
Регион |
Кластер |
|
Брянская область |
1 |
Забайкальский край |
1 |
|
Владимирская область |
1 |
Камчатский край |
1 |
|
Ивановская область |
1 |
Магаданская область |
1 |
|
Калужская область |
1 |
Еврейская автономная область |
1 |
|
Костромская область |
1 |
Чукотский автономный округ |
1 |
|
Курская область |
1 |
Республика Татарстан |
2 |
|
Липецкая область |
1 |
Краснодарский край |
2 |
|
Орловская область |
1 |
Свердловская область |
2 |
|
Рязанская область |
1 |
Ленинградская область |
2 |
|
Смоленская область |
1 |
Красноярский край |
2 |
|
Тамбовская область |
1 |
Иркутская область |
2 |
|
Тверская область |
1 |
Республика Саха (Якутия) |
2 |
|
Ярославская область |
1 |
г. Санкт-Петербург |
2 |
|
Республика Карелия |
1 |
Самарская область |
3 |
|
Республика Коми |
1 |
Саратовская область |
3 |
|
Калининградская область |
1 |
Волгоградская область |
3 |
|
Новгородская область |
1 |
Ростовская область |
3 |
|
Псковская область |
1 |
Республика Крым |
3 |
|
Республика Адыгея |
1 |
Челябинская область |
3 |
|
Республика Калмыкия |
1 |
Вологодская область |
3 |
|
Астраханская область |
1 |
Республика Дагестан |
3 |
|
г. Севастополь |
1 |
Тульская область |
3 |
|
Республика Ингушетия |
1 |
Пермский край |
3 |
|
Кабардино-Балкарская Республика |
1 |
Белгородская область |
3 |
|
Карачаево-Черкесская Республика |
1 |
Нижегородская область |
3 |
|
Республика Северная Осетия – Алания |
1 |
Кемеровская область |
3 |
|
Чеченская Республика |
1 |
Новосибирская область |
3 |
|
Республика Марий Эл |
1 |
Омская область |
3 |
|
Республика Мордовия |
1 |
Мурманская область |
3 |
|
Удмуртская Республика |
1 |
Оренбургская область |
3 |
|
Чувашская Республика |
1 |
Ставропольский край |
3 |
|
Кировская область |
1 |
Приморский край |
3 |
|
Пензенская область |
1 |
Хабаровский край |
3 |
|
Ульяновская область |
1 |
Амурская область |
3 |
|
Курганская область |
1 |
Республика Башкортостан |
3 |
|
Республика Алтай |
1 |
Сахалинская область |
3 |
|
Республика Тыва |
1 |
Архангельская область |
3 |
|
Республика Хакасия |
1 |
Воронежская область |
3 |
|
Алтайский край |
1 |
г. Москва |
4 |
|
Томская область |
1 |
Тюменская область |
4 |
|
Республика Бурятия |
1 |
Московская область |
5 |
Прокомментируем результаты кластерного анализа. Обратим внимание на то, что регионы, попавшие в одну группу, часто территориально принадлежат различным федеральным округам. Так, Чукотский автономный округ находится в одном кластере с целой группой регионов Центрального федерального округа. Это свидетельствует о том, что различия в уровне доходов населения России определяются не только спецификой территорий и климатическими условиями, в силу чего они не могут дифференцироваться только по федеральным округам.
Профили кластеров представлены в табл. 2 в виде средних значений переменных кластеризации и на рис. 1.
Таблица 2
Профили кластеров
|
Кластер |
RDD |
SDD |
NZP |
FIX |
IOK |
|
1 |
102,13 |
32240,46 |
40588,80 |
15648,08 |
36608,68 |
|
2 |
100,79 |
42606,13 |
53184,04 |
16376,78 |
293397,79 |
|
3 |
102,10 |
35709,52 |
43888,03 |
15562,56 |
137835,20 |
|
4 |
103,90 |
68466,00 |
89617,17 |
20203,35 |
1514743,93 |
|
5 |
103,90 |
54057,00 |
59305,33 |
17631,10 |
660594,60 |
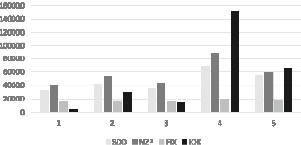
Рис. 1. Профили кластеров
Видим, что наивысшие значения всех переменных кластеризации – в регионах четвертого кластера, т.е. в г. Москве и Тюменской области. На втором месте находится единственный регион пятого кластера – Московская область. Заметим, что среди названных лидеров нет Санкт-Петербурга. Данный регион вместе с Татарстаном, Краснодарским краем, Красноярским краем, Иркутской областью и другими регионами (всего их 8) представлены во втором кластере, чьи переменные кластеризации занимают третье место в рейтинге (исключение составляет динамика реальных денежных доходов, которая в этом кластере имеет самое низкое значение). Близкими по уровню средних значений являются регионы третьего кластера (всего их 25), среди которых Белгородская область, Крым, Ростовская, Тульская, Воронежская области и другие, и регионы первого кластера (всего 46 регионов), среди которых Орловская, Костромская, Смоленская и другие области. Регионы третьего кластера все же отличает от регионов первого кластера существенное преобладание величины инвестиций в основной капитал.
В любом случае 46 регионов первого кластера характеризуются низкими значениями различных характеристик доходов и инвестиций в основной капитал. А это более половины всей России. Справедливости ради заметим, что Магаданская область, Чукотский автономный округ, Камчатский край наиболее удалены от центра первого кластера, что позволит им покинуть его при пересмотре руководством этих регионов социально-экономической политики в нужном русле. Практически в центре первого кластера находятся Брянская, Орловская, Рязанская, Смоленская, Новгородская области, Республики Карелия и Бурятия. Именно их социально-экономические показатели являются определяющими профиль первого кластера – группы регионов с низкими значениями социально-экономических показателей.
На следующем этапе нашей работы мы ввели четыре фиктивные переменные Z2, Z3, Z4, Z5 соответственно для регионов второго, третьего, четвертого и пятого кластеров. Профиль регионов первого кластера был принят за базовый, поэтому коэффициенты при фиктивных переменных в нашей модели оценят отличие средней номинальной заработной платы в регионах соответствующего кластера от ее среднего уровня для регионов первого кластера.
Приведем окончательный вид эконометрической модели:
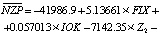 (1)
(1)
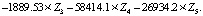
Полученное уравнение обладает неплохими качественными характеристиками:
– наблюдается высокий уровень точности модели (фактические значения NZP отличаются от расчетных (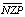 ) не более чем на 10 %);
) не более чем на 10 %);
– исправленное значение коэффициента детерминации составляет порядка 95 %, что свидетельствует о высокой доле учтенной в модели изменчивости эндогенной переменной.
Можно сделать следующие выводы, основанные на значениях параметров модели.
1. Увеличение стоимости фиксированного набора товаров и услуг в регионе на 1000 рублей должно приводить к увеличению средней номинальной заработной платы в среднем на 5137 рублей. Нарушение данного соотношения не обеспечит требуемой платежеспособности населения региона.
2. Увеличение инвестиций в основной капитал на 1 млрд рублей дает только 57 рублей в изменении номинальной заработной платы. Видим незначительное влияние. Это следовало предполагать еще при анализе корреляционной матрицы, где коэффициент парной корреляции NZP с IOK составлял всего лишь 0,45. Очевидно, что объем инвестиций в основной капитал обусловливает рост макроэкономических показателей региона, таких как валовой региональный продукт и другие, а на уровень заработной платы в регионе влияет лишь опосредованно.
3. Коэффициенты при фиктивных переменных демонстрируют отличия в среднем уровне номинальной заработной платы в соответствующем кластере от этого показателя для регионов первого кластера. Так, наибольшее отличие заработных плат регионов из первого кластера наблюдается от зарплат регионов четвертого кластера (величина отклонения порядка 58 000 рублей), по сравнению с регионами пятого кластера отличие номинальной заработной платы составляет примерно 27 000 рублей, около 7 000 рублей – отличие от заработной платы регионов второго кластера. Различия в номинальной заработной плате регионов первого и третьего кластеров несущественны.
Далее мы воспользовались нашей моделью для определения регионов, фактические уровни номинальных зарплат которых не попадают в моделируемые границы. Для этой цели были построены 95 %-ные доверительные интервалы для переменной NZP. Соответствующие результаты представлены в табл. 3 и на рис. 2.
Таблица 3
Перечень регионов с завышенным и заниженным относительно доверительного интервала уровнем NZP
|
№ п/п |
Регионы с завышенным уровнем NZP |
Регионы с заниженным уровнем NZP |
|
1 |
Брянская область |
Мурманская область |
|
2 |
Владимирская область |
Астраханская область |
|
3 |
Воронежская область |
Республика Тыва |
|
4 |
Ивановская область |
Республика Хакасия |
|
5 |
Смоленская область |
Иркутская область |
|
6 |
Калининградская область |
Кемеровская область |
|
7 |
Псковская область |
Томская область |
|
8 |
Республика Калмыкия |
Республика Бурятия |
|
9 |
Республика Крым |
Республика Саха (Якутия) |
|
10 |
Краснодарский край |
Забайкальский край |
|
11 |
Ростовская область |
Магаданская область |
|
12 |
Республика Дагестан |
Сахалинская область |
|
13 |
Кабардино-Балкарская Республика |
Чукотский автономный округ |
|
14 |
Карачаево-Черкесская Республика |
|
|
15 |
Чеченская Республика |
|
|
16 |
Ставропольский край |
|
|
17 |
Нижегородская область |
|
|
18 |
Республика Алтай |
|
|
19 |
Алтайский край |
|
|
20 |
Приморский край |
|
|
21 |
Еврейская автономная область |
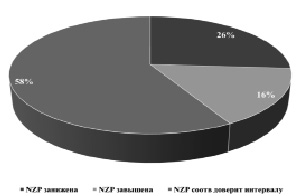
Рис. 2. Соответствие уровня номинальной заработной платы доверительному интервалу, в долях от общего количества регионов
Значительное количество регионов (21 регион (26 %)) имеют неоправданно заниженный уровень средних номинальных зарплат, что свидетельствует о необходимости серьезных изменений в политике начисления заработных плат работодателями этих областей. Стоит также отметить, что заниженный уровень заработных плат имеет место в регионах ЦФО и некоторых южных регионах, а завышенный уровень (в некоторых случаях существенно завышенный) наблюдается в северных регионах, регионах Сибири, Алтайского края и Дальнего Востока. Здесь территориальная принадлежность регионов хорошо себя проявила.
Таким образом, 13 регионов (около 16 %) демонстрируют завышенный уровень заработных плат, в 21 регионе (около 26 %) уровень зарплат занижен, в 48 регионах (58 %) уровень средней номинальной заработной платы находится в доверительном интервале (рис. 2).
Другой подход к анализу и прогнозированию номинальной заработной платы населения Российской Федерации с учетом ее региональной дифференциации состоит в применении метода квантильной регрессии [4]. В квантильной регрессии предполагается, что среднее значение 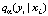 условного квантиля порядка α случайной величины Y линейно зависит от регрессоров Xj [4]
условного квантиля порядка α случайной величины Y линейно зависит от регрессоров Xj [4] 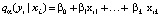 .
.
Квантильная регрессия позволяет получить иную, по сравнению с классической регрессией, информацию о поведении эндогенной переменной. Квантильная регрессия является непараметрическим методом. Она менее чувствительна к нарушению многочисленных предварительных требований, предъявляемых к исходной статистической информации в классическом регрессионном анализе [5]. Метод квантильной регрессии устойчив к аномальным наблюдениям, «выбросам» и успешно применяется при неоднородности данных. Для получения доверительного интервала прогнозных значений с уровнем доверия 1-2α достаточно воспользоваться двумя уравнениями квантильной регрессии с уровнями условного квантиля α и 1-α и в качестве доверительного интервала принять интервал значений Y, заключенный между этими двумя условными квантилями [6]. В данной работе применение квантильной регрессии позволяет подтвердить выводы, сделанные ранее, несмотря на наличие аномальных наблюдений и гетероскедастичности остатков регрессии.
Для удобства интерпретации и возможности графического представления результатов, а также учитывая небольшой вклад в регрессию переменной IOK – инвестиции в основной капитал, в качестве регрессора выберем единственную переменную FIX – стоимость фиксированного набора товаров и услуг.
Поскольку объем выборки невелик, в качестве α выберем значение 0,1, и тогда количество наблюдений, расположенных ниже уравнения квантильной регрессии с α = 0,1, как и количество наблюдений, расположенных выше уравнения квантильной регрессии с уровнем квантиля 1-α = 0,9, будет примерно равно nα = 82*0,1 ≈ 8. Результаты моделирования не противоречат полученным ранее результатам. График изменения коэффициента 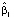 уравнения
уравнения 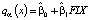 квантильной регрессии уровня α в зависимости от α приведен на рис. 3. Вычисления выполнялись в Gretl и R [7].
квантильной регрессии уровня α в зависимости от α приведен на рис. 3. Вычисления выполнялись в Gretl и R [7].
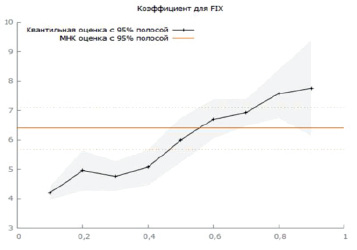
Рис. 3. График изменения коэффициента уравнения квантильной регрессии при переменной FIX в зависимости от α
Коэффициент 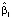 всех квантильных регрессий больше нуля. Это означает, что все квантили с ростом FIX возрастают, причем, чем больше α, тем выше скорость роста.
всех квантильных регрессий больше нуля. Это означает, что все квантили с ростом FIX возрастают, причем, чем больше α, тем выше скорость роста.
Для 10 % регионов, в которых средняя номинальная заработная плата (NZP) выше 90 % условного квантиля, вычисленного по уравнению квантильной регрессии с уровнем квантиля α = 0,9, скорость возрастания границы подмножества, определяемой 90 %-м условным квантилем NZP, равна 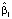 = 7,76, а для 10 % регионов с условно малым NZP, лежащим ниже вычисленного по уравнению 10 %-й квантильной регрессии значения, возрастание квантиля при возрастании FIX на единицу составляет
= 7,76, а для 10 % регионов с условно малым NZP, лежащим ниже вычисленного по уравнению 10 %-й квантильной регрессии значения, возрастание квантиля при возрастании FIX на единицу составляет 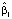 = 4,20, т.е. при увеличении FIX на единицу 10 %-й квантиль NZP, отделяющий регионы с относительно малой стоимостью набора товаров от остальных регионов, возрастает на 4,2.
= 4,20, т.е. при увеличении FIX на единицу 10 %-й квантиль NZP, отделяющий регионы с относительно малой стоимостью набора товаров от остальных регионов, возрастает на 4,2.
Это означает, что регионы с относительно высоким NZP в существенно большей степени реагируют на рост FIX. По уравнению регрессии, полученному с учетом разбиения на кластеры, скорость возрастания среднего значения NZP составляет 5,137, т.е. при увеличении FIX на 1000 рублей NZP увеличится в среднем на 5,137 тыс. рублей. Однако, как видим, на концах распределения NZP скорость изменения NZP сильно отличается от среднего значения, и при прогнозировании NZP целесообразно учитывать, принадлежит ли регион к группе с ожидаемым высоким или низким NZP.
На заключительном этапе покажем, как использовать нашу модель (1) при точечном и интервальном прогнозировании средней номинальной заработной платы в регионе при планируемых значениях включенных в нее факторов. Для примера найдем прогнозную оценку значения номинальной заработной платы в Орловском регионе (первый кластер, все фиктивные переменные модели равны нулю), если инвестиции в основной капитал увеличатся на 10 % относительно IV квартала 2019 г. и составят 36880,8 млн рублей, а стоимость фиксированного набора товаров и услуг вырастет на уровень инфляции, т.е. на 3 %, и составит 14 270 рублей. Точечный прогноз средней номинальной заработной платы в регионе и 90 %-ный доверительный интервал для заданных значений факторов представлены в табл. 4.
Таблица 4
Точечный прогноз средней номинальной заработной платы в Орловском регионе и 90 %-ный доверительный интервал
|
FIX прогнозное |
IOK прогнозное |
NZP |
||
|
Точечный прогноз |
Нижняя граница |
Верхняя граница |
||
|
14 270 |
36 880,8 |
33 415,1 |
32 111,4 |
34 718,8 |
Таким образом, прогнозируемые значения средней номинальной заработной платы вполне адекватны реальным достигнутым ранее значениям.
Заключение
В результате моделирования номинальной заработной платы с помощью двух различных методов получены схожие результаты. Оба использованных для моделирования метода позволили свести к минимуму последствия негативных для моделирования с помощью классической регрессии свойств исходной информации, таких как наличие сильно отличающихся от остальных наблюдений и наличие гетероскедастичности остатков регрессии. По итогам проведенного исследования можно сделать вывод о перспективности использования предложенных подходов для анализа и моделирования уровня средней номинальной заработной платы по региональным данным всей территории Российской Федерации с учетом региональных дифференциаций; полученную модель можно рекомендовать для использования при определении соответствия уровня средней номинальной заработной платы в регионе имеющимся или планируемым значениям включенных в нее факторов.



