Исследование взаимосвязи экономических показателей является актуальной задачей экономической науки. Ведущая роль в решении этой задачи принадлежит эконометрике. Возможности эконометрических исследований значительно расширяются с расширением возможностей вычислительной техники и развитием экономико-математических методов. В настоящее время наиболее широко применяются и развиваются методы регрессионного анализа, в котором на основе статистических данных об n наблюдениях исследуется условное среднее зависимой переменной Y от определяющих переменных X1,…, Xp, E(Y|X). В предположении, что значение Y в i-м наблюдении yi равно линейной комбинации xij значений Xj в этом наблюдении, j = 1,..,p, плюс случайный остаток εi со средним значением ноль, 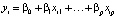 + εi, условное среднее E(yi|xi) равно
+ εi, условное среднее E(yi|xi) равно
E(yi|xi) = 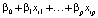 , i = 1,…,n,
, i = 1,…,n,
где xi = (1, xi1, …, xip) – i-я строка матрицы значений регрессоров X.
Вместо поиска условного среднего значения прогнозируемой переменной квантильная регрессия направлена на поиск условной медианы и любых других условных квантилей. Дополняя обычный регрессионный анализ, квантильная регрессия позволяет расширить спектр решаемых задач и тем самым получить дополнительную информацию из анализа исходной статистической информации об объекте исследования. В отличие от классической линейной регрессии, квантильная регрессия является непараметрическим методом. Она менее чувствительна к нарушению многочисленных предварительных требований, предъявляемых к исходной статистической информации в классическом регрессионном анализе [1, 2].
Цель исследования: выявление и оценка изменения степени влияния индекса цен на коэффициент рождаемости в субъектах РФ в зависимости от уровня индекса цен с помощью квантильной регрессии.
Материалы и методы исследования
В исследовании использованы данные по субъектам РФ: коэффициент рождаемости (число родившихся на 1000 человек населения) и индекс потребительских цен. Источник – Федеральная служба государственной статистики [3, 4].
Мы можем предположить наличие линейной взаимосвязи между коэффициентом рождаемости и индексом цен. При этом также можем предположить наличие гетероскедастичности в остатках, которая зачастую наблюдается в моделях, построенных по пространственным данным.
На рис. 1 приведена диаграмма рассеяния коэффициента рождаемости от индекса цен, на которой в верхней части отчетливо видны «выбросы» – наблюдения, относящиеся к регионам, имеющим аномально высокие по сравнению с другими регионами значения коэффициента рождаемости [5].
Построив линейную регрессионную модель, проверим выполнение второй предпосылки МНК, а именно, условие гомоскедастичности с помощью теста Бреуша – Пагана (функция bptest()в R).
|
library(lmtest) > fm<-lm(Y~X) > summary(fm) > # Бреуша-Пагана > bptest(fm, varformula = ~X, studentize = FALSE) |
Breusch-Pagan test
data: fm
BP = 9.5856, df = 1, p-value = 0.001961
Тестовая статистика имеет значение 9,59; p-value = 0,002 свидетельствуют о наличии гетероскедастичности, как и можно было предположить при работе с пространственными данными.
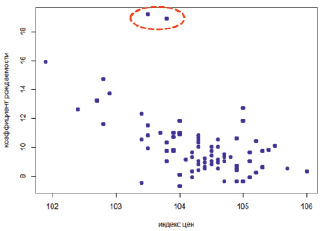
Рис. 1. Диаграмма рассеяния коэффициента рождаемости
Будем использовать метод квантильной регрессии, который относится к робастным методам, так как является устойчивым к отклонениям от предположений классических моделей. Метод квантильной регрессии устойчив к аномальным наблюдениям, «выбросам» и успешно применяется при неоднородности данных.
Напомним, что для любых θ, таких, что 0 < θ < 1, 100 θ-процентный квантиль qθ представляет собой пороговое значение, для которого случайная величина может принять меньшее значение с вероятностью θ. Функция распределения случайной величины в точке qθ принимает значение, равное θ, F(qθ) = θ.
Квантиль q(θ) можно представить как решение задачи оптимизации, минимизирующее взвешенную сумму модулей отклонений случайной величины Y от квантиля [6]
q(θ)= argmi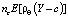 , (1)
, (1)
где ρθ(.) обозначает следующую функцию:
ρθ(y) = (θ – I (y < 0)) y = ((1 – θ) I (y < 0) +
+ θ I (y ≥ 0))y.
Индикаторная функция I (y < 0) принимает значение 1, если y < 0 и значение 0, если y ≥ 0, 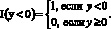
Исходя из этого, величина ρθ(y – c) принимает значение (1 – θ) | y – с |, если y < c, и значение θ|y – с|, если y ≥ c. Функция ρθ(z) является асимметричной функцией от модуля z. При этом вес (1 – θ) присваивается отрицательным z, а вес θ присваивается положительным z.
Квантильная регрессия предполагает, что условный квантиль порядка θ случайной величины Y линейно зависит от регрессоров Xj, j = 1,…,p,
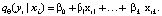 (2)
(2)
Квантильная регрессия позволяет получить иную, по сравнению с классической регрессией, информацию о поведении эндогенной переменной. Применяя её при различных значениях уровня квантиля θ, мы можем получить набор квантильных регрессий вместо единственной, получаемой с помощью метода наименьших квадратов, и тем самым мы получаем более полную картину поведения исследуемого показателя. Существенное преимущество состоит также в том, что метод квантильной регрессии не является параметрическим методом. Кроме того, квантильная регрессия устойчива к выбросам в наблюдаемых регрессорах. Она также предоставляет возможность её использования при гетероскедастичности ошибок регрессии. Это позволяет не прибегать к различным ухищрениям для ослабления влияния гетероскедастичности на оценки, тем более что это не всегда возможно.
Результаты исследования и их обсуждение
Рассмотрим задачу моделирования влияния индекса цен на коэффициент рождаемости в субъектах Российской Федерации с помощью квантильной регрессии в среде R и в Gretl.
Первая модель была получена в Gretl для квантиля 0,9 и варианта «Вычислить стандартные ошибки» при отключённом «Робастные стандартные ошибки / интервалы».
Модель 1: Квантильная оценка, использованы наблюдения 1-82
Зависимая переменная: Y
tau = 0,9
|
Коэффициент |
Ст. ошибка |
t-статистика |
P-значение |
||
|
const |
193,497 |
45,9010 |
4,216 |
<0,0001 |
*** |
|
X |
−1,74286 |
0,440091 |
−3,960 |
0,0002 |
*** |
|
Медиана зав. перемен |
9,650000 |
Ст. откл. зав. перемен |
2,143853 |
|
|
Сумма модулей ошибок |
169,9286 |
Сумма кв. остатков |
487,2063 |
Уравнение квантильной регрессии порядка τ = 0,9 имеет вид
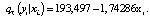
Все коэффициенты модели значимы. Выборочный коэффициент регрессии 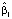 при xi отрицательный,
при xi отрицательный, 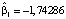 . Это означает, что для 10 % регионов, в которых коэффициент рождаемости находится выше предсказанного по 90 %-му уравнению квантильной регрессии, повышение индекса цен на единицу приводит в среднем к падению коэффициента рождаемости на 1,74.
. Это означает, что для 10 % регионов, в которых коэффициент рождаемости находится выше предсказанного по 90 %-му уравнению квантильной регрессии, повышение индекса цен на единицу приводит в среднем к падению коэффициента рождаемости на 1,74.
В меню Модель1 при выборе Анализ/Матрица коэффициентов ковариации была получена автоковариационная матрица, на главной диагонали которой находятся дисперсии коэффициентов регрессии:
|
const |
X |
|
|
const |
2106,9 |
-20,2 |
|
X |
-20,2 |
0,19368 |
Вектор оценок коэффициентов квантильной регрессии  имеет асимптотически нормальное распределение. В протоколе модели 1 приведены стандартные ошибки параметров
имеет асимптотически нормальное распределение. В протоколе модели 1 приведены стандартные ошибки параметров 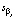 (
(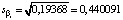 ) и соответствующие t-статистики. Далее доверительные границы параметров получаются в виде
) и соответствующие t-статистики. Далее доверительные границы параметров получаются в виде 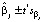 , где t* ‒ критическое значение для заданного уровня значимости. Эти доверительные границы можно получить при выборе в меню Окно модели/Анализ/Доверительные интервалы для коэффициентов:
, где t* ‒ критическое значение для заданного уровня значимости. Эти доверительные границы можно получить при выборе в меню Окно модели/Анализ/Доверительные интервалы для коэффициентов:
t(80, 0,025) = 1,990
|
Переменная |
Коэффициент |
95 доверительный интервал |
|
const |
193,497 |
(102,151, 284,843) |
|
X |
-1,74286 |
(-2,61867, -0,867049) |
Gretl и R предоставляют возможность получения доверительных интервалов 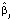 разными способами. Коэффициенты квантильной регрессии для всех методов одинаковые. Различаются лишь 5 %-ные доверительные интервалы коэффициентов. Они получены при разных допущениях относительно отклонений от регрессии. В основном рассматриваются 3 варианта предположений относительно отклонений: независимые одинаково распределённые (i.i.d), не независимые одинаково распределённые (n.i.d), независимые неодинаково распределённые (i.ni.d). К тому же предоставляется возможность выбора робастных или неробастных методов оценки. Выбор того или иного допущения предоставляется пользователю.
разными способами. Коэффициенты квантильной регрессии для всех методов одинаковые. Различаются лишь 5 %-ные доверительные интервалы коэффициентов. Они получены при разных допущениях относительно отклонений от регрессии. В основном рассматриваются 3 варианта предположений относительно отклонений: независимые одинаково распределённые (i.i.d), не независимые одинаково распределённые (n.i.d), независимые неодинаково распределённые (i.ni.d). К тому же предоставляется возможность выбора робастных или неробастных методов оценки. Выбор того или иного допущения предоставляется пользователю.
В Gretl можно задать не один квантиль, а список квантилей. В этом случае будут вычислены оценки коэффициентов квантильной регрессии, их стандартные ошибки и доверительные интервалы для каждого из указанных значений.
При выдаче протокола Наблюдаемые и расчетные значения некоторые наблюдения помечаются * – это означает, что ошибка квантильной регрессии для этого наблюдения выходит за пределы 2,5 единиц стандартных ошибок. В нашем случае – это 3 наблюдения: 42 (Чеченская Республика) и 63 (Республика Тыва) имеют коэффициент рождаемости существенно выше предсказанного для данной группы регионов с высокой рождаемостью, а для 46-го наблюдения (Республика Мордовия) коэффициент рождаемости значительно ниже ожидаемого. Это явно аномальные наблюдения. Для классической регрессии они бы сильно повлияли на результаты моделирования, а для квантильной регрессии не имеет значения, насколько велико отклонение yi от ожидаемого значения, имеет значение только факт принадлежности наблюдения к данной группе.
Далее воспользуемся возможностью построения серии моделей квантильной регрессии с различными значениями квантилей, указав квантили от 0,1 до 0,9 с шагом 0,1 (Модель 3).
Модель 3: Квантильная оценка, использованы наблюдения 1-82
Зависимая переменная: Y
Асимптотические стандартные ошибки считаются независимыми и одинаково распределенными
tau Коэффициент Ст. ошибка t-статистика
-------------------------------------------------------
const 0,100 127,600 32,0240 3,98452
0,200 139,275 23,3508 5,96446
0,300 139,625 17,0092 8,20881
0,400 154,378 23,1615 6,66528
0,500 137,300 29,7506 4,61503
0,600 159,143 27,6001 5,76603
0,700 155,306 27,8035 5,58583
0,800 167,250 34,2478 4,88352
0,900 193,497 45,9010 4,21553
X 0,100 -1,14286 0,307040 -3,72218
0,200 -1,25000 0,223883 -5,58327
0,300 -1,25000 0,163081 -7,66491
0,400 -1,38889 0,222068 -6,25434
0,500 -1,22222 0,285244 -4,28483
0,600 -1,42857 0,264625 -5,39848
0,700 -1,38889 0,266575 -5,21013
0,800 -1,50000 0,328362 -4,56813
0,900 -1,74286 0,440091 -3,96022
Изменение значений коэффициента 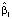 моделей в зависимости от значения квантиля τ приведено на рис. 2.
моделей в зависимости от значения квантиля τ приведено на рис. 2.
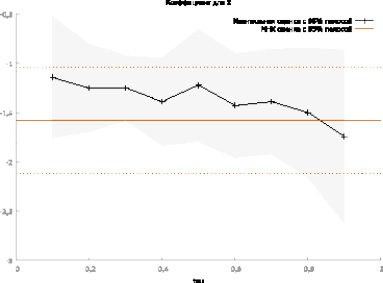
Рис. 2. Изменение значений коэффициента 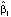
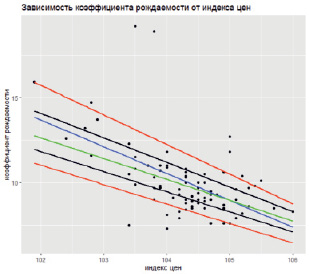
Рис. 3. Графики квантильных регрессий при пяти различных τ и график классической регрессии
Коэффициент 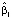 всех квантильных регрессий меньше нуля. Это означает, что все квантили с ростом индекса цен убывают, причём чем больше τ, тем скорость убывания больше. Для 10 % регионов, в которых коэффициент рождаемости выше 90 % условного квантиля, вычисленного по уравнению квантильной регрессии с уровнем квантиля τ = 0,9, скорость убывания границы подмножества, определяемой 90 %-ным условным квантилем коэффициента рождаемости, равна
всех квантильных регрессий меньше нуля. Это означает, что все квантили с ростом индекса цен убывают, причём чем больше τ, тем скорость убывания больше. Для 10 % регионов, в которых коэффициент рождаемости выше 90 % условного квантиля, вычисленного по уравнению квантильной регрессии с уровнем квантиля τ = 0,9, скорость убывания границы подмножества, определяемой 90 %-ным условным квантилем коэффициента рождаемости, равна 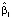 = -1,74 , а для 10 % регионов с условно низким коэффициентом рождаемости, лежащим ниже вычисленного по уравнению 10 %-ной квантильной регрессии значения, убывание квантиля при возрастании индекса цен на единицу составляет
= -1,74 , а для 10 % регионов с условно низким коэффициентом рождаемости, лежащим ниже вычисленного по уравнению 10 %-ной квантильной регрессии значения, убывание квантиля при возрастании индекса цен на единицу составляет 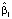 = -1,14, то есть при увеличении индекса цен на единицу 10 %-ный квантиль коэффициента рождаемости, отделяющий регионы с низкой рождаемостью от остальных регионов, уменьшится на 1,14. Это означает, что регионы с относительно высокой рождаемостью в существенно большей степени реагируют на рост индекса цен. По уравнению регрессии, полученному с помощью метода наименьших квадратов (МНК)), скорость убывания среднего значения коэффициента рождаемости составляет -1,577, то есть при увеличении индекса цен на 1 коэффициент рождаемости уменьшится в среднем на -1,577. Однако, как видим, на концах распределения коэффициента рождаемости скорость изменения коэффициента рождаемости сильно отличается от среднего значения и при прогнозировании коэффициента рождаемости целесообразно учитывать, принадлежит ли регион к группе с высокой или низкой рождаемостью.
= -1,14, то есть при увеличении индекса цен на единицу 10 %-ный квантиль коэффициента рождаемости, отделяющий регионы с низкой рождаемостью от остальных регионов, уменьшится на 1,14. Это означает, что регионы с относительно высокой рождаемостью в существенно большей степени реагируют на рост индекса цен. По уравнению регрессии, полученному с помощью метода наименьших квадратов (МНК)), скорость убывания среднего значения коэффициента рождаемости составляет -1,577, то есть при увеличении индекса цен на 1 коэффициент рождаемости уменьшится в среднем на -1,577. Однако, как видим, на концах распределения коэффициента рождаемости скорость изменения коэффициента рождаемости сильно отличается от среднего значения и при прогнозировании коэффициента рождаемости целесообразно учитывать, принадлежит ли регион к группе с высокой или низкой рождаемостью.
Ниже приведены графики квантильных регрессий при τ, равных 0,1; 0,25; 0,5; 0,75; 0,9 и график классической регрессии для условного среднего Y.
С помощью такого рода графиков можно строить доверительные границы для предсказанных значений yi. Графики всех квантильных регрессий почти параллельны. Третий сверху график относится к классическому уравнению регрессии. Угловой коэффициент графика смещён, вероятно, под влиянием аномальных наблюдений, и потому этот график пересекается с графиком медианной регрессии. В данном случае прогнозировать значения yi предпочтительней по медианной регрессии.
Заключение
В заключение ещё раз подчеркнём, что квантильная и классическая регрессии не конкурируют между собой, а взаимно дополняют друг друга. Они отвечают на разные вопросы. Если в центре внимания классической регрессии лежит математическое ожидание условного среднего в зависимости от того, какое значение примет определённый набор параметров, называемых регрессорами, то в квантильной регрессии изучается математическое ожидание условных квантилей случайной величины в зависимости от того, какое значение примет набор регрессоров.



