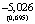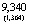Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Достоинством моделей векторной авторегрессии является простота их использования, точность прогнозов, сопоставимая с точностью сложных макроэкономических моделей, отсутствие каких-либо структурных или идентификационных ограничений на параметры. Однако последняя их особенность приводит к слабой экономической обоснованности и проблеме сверхпараметризации. Проблема сверхпараметризации может быть решена при помощи байесовского подхода, применительно к модели VAR. А проблема интерпретации функций импульсных откликов, получаемых на основе VAR(p)-моделей, решается переходом к моделям структурной векторной авторегрессии (SVAR). При построении таких моделей на шоки векторной авторегрессии структурной формы VAR накладываются ограничения по аналогии с моделями систем одновременных уравнений (СОУ), что и позволяет получить функции импульсных откликов, имеющие экономическое обоснование [1, 2]. В последние десятилетия модели SVAR используются как стандартная и универсальная процедура, явно учитывающая взаимосвязи между переменными и повышающая точность и надёжность оценок по сравнению с моделями VAR [3].

Основная цель данной работы состоит в сравнительном анализе результатов оценивания макроэкономических показателей в рамках современных модификаций моделей векторной авторегрессии, нашедших широкое применение в практике краткосрочного прогнозирования: классической модели векторной авторегрессии (VAR) (модель без ограничений на параметры), байесовской модели векторной авторегрессии (BVAR) (модель с ограничениями на параметры) и модели структурной векторной авторегрессии (SVAR) (модель с ограничениями на параметры). В качестве показателя эффективности рассматривается стандартная ошибка модели. Результаты оценивания моделей VAR и BVAR с применением программной среды R приведены в работе [4]. В данной статье уделяется внимание моделям SVAR и реализации их алгоритмов оценивания и анализа в программной среде R.

Спецификация и идентификация моделей SVAR

Структурная форма VAR (как и рекурсивная) учитывает в явном виде одновременные взаимодействия между элементами вектора переменных модели добавлением к правой части спецификации члена, относящегося к текущему моменту времени. Для идентифицируемости матрицы коэффициентов этого члена вводятся некоторые ограничения: в рекурсивной VAR – это механическая процедура, учитывающая порядок включения переменных в спецификацию, в структурной форме VAR для задания порядка одновременных связей между переменными используются предпосылки экономической теории. Спецификация модели SVAR(p), как модификация модели VAR(p) приведенной формы,

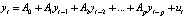, (1)

принимает вид

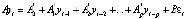, (2)

где ошибки структурной формы εt – вектор ненаблюдаемых структурных шоков (белый шум) с автоковариационной матрицей Σε, B – матрица зависимости между структурными шоками, ut – вектор остатков приведенной VAR(p)-модели не имеющий экономической интерпретации,

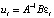, (3)

с автоковариационной матрицей

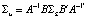. (4)

Взаимосвязь структурных и приведенных параметров модели выполняется по правилу:

, ,

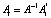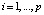где Ai – (m×m)-матрица приведенных параметров с единицами на главной диагонали, 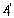– (m×m)-матрица структурных параметров. Спецификация VAR(p)-модели в форме бесконечного векторного скользящего среднего (представление Вольда):

,

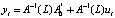где

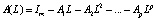
– оператор авторегрессии порядка p, используется при анализе эффектов влияния шоковых воздействий одних переменных на другие, однако динамические отклики не обладают экономическим смыслом. Учитывая взаимосвязь (3) между приведенными и структурными шоками, можно получить информацию о структурных шоках, с учетом ограничений, накладываемых в рамках модели SVAR на приведенные шоки. Таким образом, SVAR-модель может быть использована, как и модель VAR, для исследования влияния шоков путем наложения ограничений на матрицы A и/или B в модели (2).

В качестве идентифицирующих ограничений используются: ограничения на параметры одного уравнения (условия нормализации); ограничения на параметры нескольких структурных уравнений (например, выбор рекурсивной спецификации системы уравнений); ограничения на структуру автоковариационной матрицы возмущений (например, ортогональность возмущений). В SVAR рассматриваются три типа моделей: A-модель – ограничения накладываются на матрицу B (B = Im), с минимальным для идентификации числом ограничений – m(m – 1)/2; B-модель – ограничения накладываются на матрицу A (A = Im), с минимальным для идентификации числом ограничений – m(m – 1)/2; AB-модель – ограничения могут быть наложены на обе матрицы (минимальное количество ограничений для идентификации составляет m2 + m(m – 1)/2), где I – единичная матрица, m – число эндогенных переменных модели.

Модель SVAR – оценивается методом максимального правдоподобия с функцией правдоподобия вида 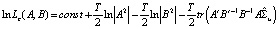[5]:

, (5)

где 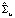– оценка автоковариационной матрицы остатков приведенной модели VAR(p). При формировании целевой функции метода, к функции правдоподобия (5) добавляют ограничения на структурные параметры.

Для тестирования сверхидентифицируемости ограничений на структурные параметры используется тест отношения правдоподобия:

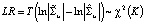, (6)

где 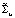– оценка автоковариационной матрицы вектора возмущений модели SVAR без ограничений на параметры, 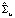– оценка автоковариационной матрицы вектора возмущений модели SVAR с ограничениями на структурные параметры, K – число ограничений на структурные параметры.

SVAR(p)-модели в программной среде R

В программной среде R в пакете vars для оценки модели SVAR используются два метода. Первый метод применяет функцию optim () для прямой минимизации отрицательной функции логарифмического правдоподобия (5), тогда как второй метод использует алгоритм оценки scoring, предложенный в работе [6]. Для выбора метода (аргумент «estmethod» в функции SVAR()) используются параметры: «direct» или «scoring» соответственно. Первый аргумент в функции SVAR () должен быть объектом класса varest (оцениваемый при помощи функции VAR() пакета vars). Выбор A-, B- или AB-модели определяется параметрами: Amat и Bmat соответственно. Если оценивается A-модель, то задаются параметры Amat, Bmat = NULL (в этом случае Bmat приравнивается к единичной матрице, размером m×m). Если оценивается B-модель, то задаются параметры Bmat, Amat = NULL (в этом случае Amat приравнивается к единичной матрице, размером m×m). В зависимости от выбранной модели, в качестве выходной информации в протоколе приводятся элементы матрицы A и их стандартные ошибки Ase, элементы матрицы B и их стандартные ошибки Bse.

При использовании метода estmethod = = «direct» стандартные ошибки возвращаются только в том случае, если в функции SVAR() указать параметр hessian = TRUE. Возвращённый элемент Sigma.U представляет собой оценку автоковариационной матрицы приведенной формы (4), умноженную на 100: 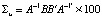. Эта оценочная матрица соответствует аналогу матрицы в приведенной форме только в том случае, если SVAR-модель точно идентифицируема.

Функция summary(svar.A) формирует протокол, включающий: название функции с параметрами; тип модели; размер выборки; значение логарифмической функции правдоподобия; метод оценки параметров; количество итераций; статистику теста отношения правдоподобия на значимость ограничений на структурные параметры SVAR модели; оценку элементов матрицы A; оценку стандартных ошибок элементов матрицы A; элементы матрицы B; оценку автоковариационной матрицы вектора возмущений приведенной формы, умноженную на 100.

Для анализа причин и эффектов влияния одних переменных на другие в VAR-моделях используется функция импульсного отклика. В случае если элементы вектора возмущений ut коррелированы, шоки оказывают не изолированные воздействия на выбранные переменные, а влияют на все другие элементы вектора эндогенных переменных модели. Возникают затруднения с интерпретацией данных функций. Для преодоления этой проблемы в эконометрических пакетах применяется ортогональная функция импульсного отклика. Для построения функции импульсной отдачи в R используется функция irf() пакета vars с основными параметрами: varfit – объект, сформированный при помощи функции VAR(); impulse – импульс – переменная, воздействие которой изучается; response – отклик – переменная, на которую оказывается воздействие; Вычисление ортогонализированных или кумулятивных функций импульсного отклика задаётся параметрами ortho и cumulative соответственно. Длина импульсных откликов устанавливается параметром n.ahead, по умолчанию принимаемым 10 периодам упреждения.

В программной среде R имеется возможность вычисления функций импульсного отклика не только для объектов класса varest (в рамках моделей VAR), но также и для объектов класса svarest (в рамках моделей SVAR) с одним и тем же набором аргументов, за исключением параметра ortho, который необходим для решения проблемы интерпретации результатов значений функций импульсного отклика в моделях VAR().

SVAR(p)-модель: оценка на эмпирических данных

Для построения модели SVAR воспользуемся данными макроэкономических показателей: расходы на конечное потребление (Y) и валовое накопление (X) в РФ. В табл. 1 приводятся годовые данные показателей за период с 1991 по 2019 г. включительно (в млрд руб.) [7].

Макроэкономические ряды Y и X нестационарны. Поэтому в качестве первичной обработки они были подвергнуты логарифмированию и вычислению разностей первого порядка. Преобразованные переменные y и x, практически показывающие процентное изменение динамики исходных показателей, являются стационарными и используются в качестве исходных переменных при построении модели VAR. По данным табл. 1 была оценена модель VAR(2) [4]:

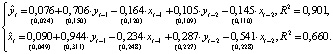(8)

Для оценки структурных параметров модели SVAR(2) воспользуемся функцией SVAR () пакета vars и оценим параметры A-модели. Для оценки параметров модели выберем первый метод – метод прямой минимизации отрицательной функции логарифмического правдоподобия, задавая в качестве аргумента функции SVAR(): estmethod = «direct».

В табл. 2 приводятся результаты оценивания структурных параметров – элементы матрицы А и их стандартные ошибки.

Оценки параметров статистически значимы. Нулевая гипотеза о сверхидентифицируемости ограничений на структурные параметры отклоняется (тест отношения правдоподобия (6)),

.

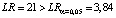Таблица 2

SVAR A-модель: оценки параметров

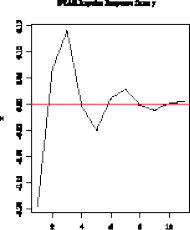
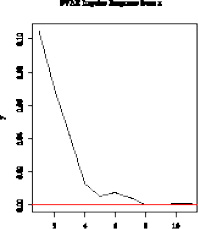
В табл. 3 представлены графики функций импульсного отклика переменных модели SVAR, построенные в программной среде R при помощи функции plot(irf.svarA), основным параметром которой является результат оценивания функции irf() импульсной отдачи.

Следует отметить, что шок в динамике переменной y (процентное изменение расходов на конечное потребление) вызывает резкое возрастание переменной x (процентное изменение валового накопления), а затем затухание. Шок в динамике переменной x (процентное изменение валового накопления) вызывает резкое уменьшение переменной y (процентное изменение расходов на конечное потребление), а затем затухание.

Заключение

В табл. 4 приводятся стандартные ошибки моделей VAR(2), BVAR(2) и SVAR(2), включающих две переменные.

Таблица 4

Стандартные ошибки моделей VAR, BVAR и SVAR

Из табл. 4 следует, что для оцененных моделей стандартные ошибки SVAR(2) сопоставимы со стандартными ошибками VAR(2), стандартные ошибки модели BVAR(2) на порядок точнее. Такой результат объясняется малым объемом выборочных данных, на котором очевидны преимущества байесовского оценивания.