Социология долго рассматривалась как гуманитарная наука. Если учесть, что многие социальные проблемы в обществе тесно переплетаются с экономической структурой и проблемами экономики, то ситуация с гуманитарным подходом просто неприемлема и требует формализованного исследования вплоть до цифровизации описания социально-экономических систем (СЭС). Может встать вопрос о возможности построения математических моделей в таком океане данных и их взаимосвязей для СЭС. Однако важно, чтобы были сделаны первые шаги в формализации моделей функционирования СЭС, чтобы начать использовать формальные правила и закономерности, установленные другими исследованиями. Последующее усложнение моделей становится проще и даёт больше возможностей для анализа и прогнозирования поведения в моделях СЭС [1, 2].
В настоящее время достигнут гигантский прогресс в накоплении большого объёма социально-экономических «больших данных» (БД) с помощью цифровых технологий в различных форматах в таком виде, как числовые, текстовые данные, изображения, музыка и другие типы трудно формализуемой информации. Появились мощные суперкомпьютеры, объединяющиеся с помощью интернета и современных программ обработки БД в «облачные технологии» с широчайшими возможностями расчёта результатов для моделей из систем с десятками уравнений. Перед наукой, которая включает в себя построение математических моделей в социально-экономической области; объяснение сложных явлений в обществе в областях экономики и социологии, открываются определённые перспективы [1–3].
Источником, питающим идеями прогресс в развитии моделей СЭС, является синергетика. Синергетические модели представляют собой систему дифференциальных уравнений для существенных переменных СЭС, называемых параметрами порядка (ПП), с квазиравновесными параметрами, которые определяют влияние внутрисистемных и внешних факторов на изменения со временем ПП. Модель, описывающая системы и процессы в них, может быть получена как система дифференциальных уравнений в фазовом пространстве системы. Система медленно релаксирующих параметров и будет определять набор дифференциальных уравнений для ПП, образующих её синергетическую модель [2–4].
При изучении динамических процессов развития рынков ресурсов часто используют методы теории исследования операций или системы линейных квазиравновесных уравнений баланса. Принцип оптимальности не описывает автоколебания параметров в неравновесных СЭС, наличие у них быстрых изменений и скачков. СЭС являются открытыми и неравновесными, участвуя в активном обмене ресурсами, информацией и энтропией друг с другом и с окружением. Обмен СЭС энтропией со средой может приводить к её локальному понижению, что связано со структурными изменениями и образованием новых форм организации и функционирования. В структуре поведения, как правило, возникают процессы бифуркаций, переходящие в хаос с последующей самоорганизацией новых оптимальных структур. Эволюционное и стохастическое развитие синергетических открытых многосекторных моделей СЭС как системы дифференциальных уравнений для основных ПП экономики рассматривалось в [2, 3].
Задачей анализа является исследование возможных сценариев изменения социально-экономических систем с учётом различных социальных факторов. В поведении СЭС зачастую возникают хаотические состояния, описываемые странными аттракторами, с фрактальной структурой, имеющими дробную фрактальную размерность и меняющими её с течением времени. Хаотические структуры в фазовом пространстве могут превращаться со временем в циклические колебания экономических и социальных параметров, показывают превращение фазовых траекторий в поведение типа устойчивого или неустойчивого фокусов. Целью управления СЭС являются требования обеспечения такого характера поведения переходных процессов, которые приводят к желаемому аттрактору и обеспечение желаемого асимптотического, эволюционного движения в этом аттракторе [2, 3, 5].
Методы исследования процессов в социально-экономических системах
Естественным способом описания процессов в природе и обществе, предсказывающим будущее по известным начальным состояниям параметров, являются дифференциальные уравнения. В динамических, связанных, нелинейных, дифференциальных уравнениях с параметрами возможны так называемые бифуркации, катастрофы, делающие их поведение непредсказуемым, поэтому целесообразно их использовать при выборе моделей СЭС. Особенностью СЭС заключается в существовании большого числа скрытых управляющих параметров. Выявление этих параметров и их изменений входит в задачу верификации используемых моделей и позволяет предсказывать следствия изменения этих параметров для СЭС [1–3]. Полагаем, что состояние СЭС характеризуется векторной переменной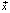 
, компоненты которой являются ПП системы, и некоторым управляющим n-мерным параметром 
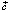, изменение которого влияет на поведение 
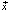. Пространство изменения параметров 
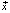и 
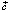– это фазовое пространство.
Изменение во времени переменной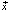 
характеризуется скоростью 
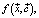значение которой в градиентном приближении можно выразить через потенциал СЭС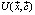 
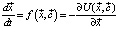, (1)
где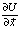 
– градиент потенциала U системы n динамических, связанных, нелинейных, дифференциальных уравнений. Проведём исследования нелинейных дифференциальных уравнений (1) с параметрами в рамках теории катастроф и бифуркационного анализа. При изменениях системы вдоль фазовой траектории необходимо исследовать равновесные состояния, которые определяются уравнением для точки с нулевой скоростью
f(x(с), с) = 0. (2)
При управляющем параметре c однозначное разрешение уравнения (2) даёт кривую равновесных стационарных состояний системы x = x(c). Естественное изменение среды и, следовательно, параметра c ведёт к процессу появления последовательности квазиравновесных состояний. В связи с этим возникает вопрос устойчивости системы в процессе этой медленной эволюции. Ответ на этот вопрос даёт теорема Ляпунова [1, 5]. При нарушении условий разрешимости уравнения стационарности (2) в точке (x0, c0) возможно появление новой стационарной ветви решения (2) в фазовом пространстве, т.е. происходит бифуркация (раздвоение) кривых равновесия [2, 4, 5].
При изменении управляющих параметров модели ci возможно появление тройных, четверных и т.д. критических точек, т.е. возникновение других ветвей решения модели (1). В связи с этим в теории бифуркации приходится решать вопрос о возможных сменах моделей функционирования и смене структур СЭС. Таким образом, переход систем через критические точки c0 при изменении параметров ci сопровождается иногда неоднозначностью выбора дальнейшего поведения систем. Ситуация осложняется появлением со временем у части ветвей структурной неустойчивости. Поскольку вблизи критических точек системы входят в область сильных флуктуаций параметров, это делает возможным появление череды неустойчивостей и, следовательно, трудностей с управлением системами. Компьютерное моделирование показывает, что возникающие хаотические бифуркации (неустойчивости), как правило, чередуются со значительными интервалами спокойного эволюционного развития [5–7].
Следствием сделанных общих утверждений бифуркационного поведения нелинейных синергетических моделей СЭС является схема работы: во-первых, необходимо проведение бифуркационного анализа, состоящего в выявлении стационарных критических точек на фазовых траекториях; выявлении наличия устойчивых и неустойчивых ветвей при прохождении критических точек; во-вторых, проведение анализа на устойчивость траекторий моделей СЭС после прохождения критических точек. Систематизация критического поведения, бифуркаций и типов элементарных катастроф, представленных в теории катастроф [1, 4, 5].
Рассмотрим модели СЭС как систему нелинейных уравнений возрастающего порядка по степеням параметров порядка систем. Простейшие уравнения для управления ресурсами получены нами ранее при учёте в синергетическом потенциале уравнения (1) нелинейностей ПП степени 2, которые описываются катастрофой «складка» и возникают в производственных моделях управления ресурсами и моделях экологии [1–3]. Такой моделью управления ресурсами является логистическая модель. Была предложена «мягкая» модель управления ресурсами, в которой управляющие параметры логистической модели сами линейно зависят от исследуемых ресурсов, обеспечивая обратную связь в системе. В этом случае исчезает неустойчивость «жёсткой» модели и появляется устойчивая к малым изменениям параметров в «мягкой» модели вблизи критических, стационарных точек (2), что было показано на примере управления трудовыми ресурсами в модели катастрофы «складка» [2, 8].
Многие социально-экономические явления в СЭС, имеющие характер скачков параметров или на языке синергетики катастроф, происходят в моделях, учитывающих более высокие члены разложения синергетического потенциала U в уравнении (1) по малым значениям ПП вблизи стационарных критических точек. Пример катастроф типа (бунт, забастовка) были рассмотрены ранее с учётом нелинейностей четвёртого порядка по ПП в модели катастрофы «сборка» [1, 2, 4]. Синергетический потенциал (1) может иметь вид
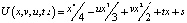. (3)
Заменой переменных x = y – a/3 в потенциале (3) уравнения (1) приводится к виду
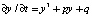. (4)
В стационарной критической точке уравнение (3) можно записать в виде
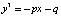, (5)
где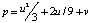 
, 
.
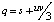Уравнение (5) решается численно в любом математическом пакете с визуализацией, поскольку стационарные точки находятся на пересечении чистой кубической параболы с линией, что имеем в уравнении (5) (рис. 1). Наклон и сдвиг линии определяются параметрами p и q и зависят от управляющих параметров исходного синергетического потенциала (3). При определённых параметрах x потенциала ПП испытывает скачок типа фазового перехода первого рода из одной устойчивой стационарно точки в другую. Что в конкретном случае с забастовкой означает скачок забастовочного движения. Большие трудности представляет процесс нахождения управляющих параметров для конкретных СЭС.
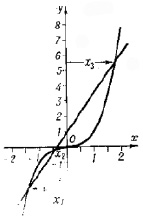
Рис. 1. Графическое решение уравнения (4)
Рассмотрение более сложных нелинейностей параметров СЭС вблизи критических точек приводит к необходимости рассмотрения нелинейных уравнений более высоких пятых и т.д. степеней по ПП. Учёт в синергетическом потенциале этих нелинейностей приводит к синергетическому уравнению для катастрофы типа «ласточкин хвост» для уравнения (1), где
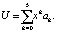(6)
Заменой переменных x = y – a/4 приведём (1) к виду
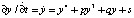. (7)
Уравнение для стационарных критических точек получим при равном нуле левой части уравнения (7):
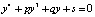. (8)
Уравнение (8) можно заменить системой уравнений
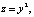
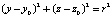. (9)
В системе уравнений (9)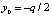 
, 
, 
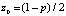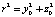. Первое уравнение системы (9) – чистая квадратичная парабола. Второе уравнение даёт окружность радиуса r, параметры которой зависят от коэффициентов уравнения (7) (рис. 2). Стационарные точки модели получаем как пересечения этих двух фигур на плоскости (y–x). Управляющие параметры синергетического потенциала входят в определение параметров окружности. Окружность при определённых параметрах может иметь пересечение с параболой в четырёх точках, в трёх точках и в двух, как на рис. 2. Четыре точки пересечения фигур на рис. 2 соответствуют четырём стационарным точкам уравнения (8). При касании окружности и параболы происходит слияние устойчивой и неустойчивой стационарных точек с возможным последующим их исчезновением.
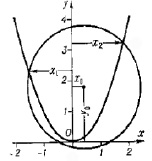
Рис. 2. Графическое решение системы уравнений (9)
Для выявления устойчивых и неустойчивых ветвей при прохождении критических точек необходимо проведение анализа на устойчивость траекторий моделей СЭС в критических точках. Наша модель учитывает нелинейные члены до пятого порядка в синергетическом потенциале, поэтому охватывает модели, относящиеся к катастрофам типа «ласточкин хвост» [1, 5].
Задача качественного исследования устойчивости и неустойчивости моделей СЭС дифференциальными уравнениями (1) сводится к исследованию функции скорости изменения ПП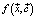 
. Теорема Ляпунова формулируется для функции Ляпунова, которой в случае уравнения (1) является синергетический потенциал U. Минимум в любой точке фазовой траектории, в том числе и стационарной точке a, по Ляпунову определяется минимумом синергетического потенциала 
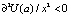[1, 4, 5]. Это даёт возможность определить минимум или максимум функции в стационарной точке с помощью функции фазовой скорости в виде: (∂f(a))/(∂x < 0) при минимуме и (∂f(a))/(∂x > 0) для максимума. Убывание функции Ляпунова в окрестности точки a свидетельствует о наличии минимума фазовой траектории при эволюционном движении в области существования гладких функций до следующей стационарной точки, в которой производная изменит знак.
Поскольку синергетический потенциал является и функцией Ляпунова то устойчивыми точками являются точки A, в которых выполняется условие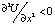 
. Точки А являются аттракторами, и квазистационарные фазовые траектории СЭС движутся эволюционно от неустойчивых стационарных точек В к аттракторам А внутри заштрихованных областей в направлении стрелок рис. 3. Заштрихованные области представляют собой точки фазового пространства системы, ограниченные сверху кривой полинома (6) со степенями членов k > 1 и коэффициентами (а2 = 1.2, а3 = -1.85, а4 = 0.94, а5 = -0.15) (на диаграмме рис. 3 ряд 1) и линией у = kx с (к = 0.07) (на диаграмме рис. 3 ряд 2). При создании рис. 3 мы воспользовались идеей Арнольда [8] и ввели обратную связь в уравнении (1) с потенциалом (6), стабилизирующую отклики системы [8, 9]. Точки внутри заштрихованных областей удовлетворяют условию (2). Скорость эволюционного движения вдоль фазовой кривой происходящего внутри заштрихованного пространства определяется производной 
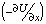. В остальных точках фазового пространства происходит быстрая хаотизация траектории с последующими бифуркациями до достижения устойчивых точек или областей. Особенность бифуркационной диаграммы (рис. 3) состоит в появлении разделённых различных «технологических» областей. Системы с такой нелинейностью исследовались нами ранее при возникновении финансовых корпораций и банкротстве банков в финансовом рыночном секторе экономик [1–3].
Заключение
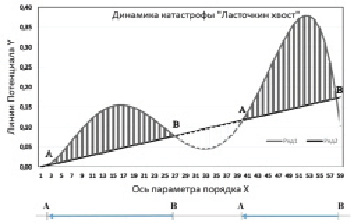
Рис. 3. Исследование устойчивости стационарности потенциала (6)
Становятся привычными исследования динамического хаоса, фрактальных структур и диссипативных синергетических моделей в СЭС. Синергетика уже занялась процессом моделирования экономики и социальных проблем общества. Здесь мы сталкиваемся с такими процессами, как зарождение более адекватного сообществу социального и экономического порядка в виде революции, бунта, которые зарождаются сначала как идея в виде флуктуации. Хаос фактически становится инструментом разрушения старых структур и порождением новой упорядоченности в структуре идеологии и экономике общества.
Впечатляющими будут результаты применения искусственного интеллекта в стратегическом историковедении и компьютерном прогнозировании в общественных науках. Уже видны перспективы использования искусственного интеллекта в синергетическом моделировании экономико-социальных явлений. Претендующими на эту роль являются облачные технологии обработки «больших данных» (БД). При верификации предлагаемых синергетических моделей СЭС приходится заниматься обработкой больших объёмов данных. Обработка БД в распределённой вычислительной среде через интернет проводится с использованием таких технологий, как MapReduce и Hadoop. Они позволяют быстро описать и тестировать распределённые системы, проводить эффективное, автоматическое распределение данных и работы между машинами с использованием внутреннего параллелизма процессорных ядер [2, 4, 5].