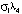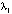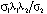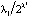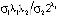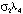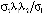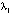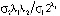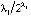Векторные авторегрессионные модели (VAR), предложенные К. Симсом в 1980 г., являются классическим инструментом анализа динамики нескольких связанных друг с другом временных рядов. Преимущество классической модели VAR по сравнению с системами одновременных уравнений (СОУ) в структурной форме состоит в отсутствии необходимости априорных ограничений, гарантирующих идентификацию. Спецификация модели VAR(p) для m-мерного вектора переменных модели Yt имеет вид [1]:
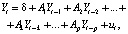(1)
где Ak – (m×m)-матрица, k = 1,..., p – величина лага, ut – m-мерный вектор с (m×m)-ковариационной матрицей Ω и нулевым математическим ожиданием,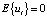 
, δ – m-мерный вектор свободных членов. Система (1), с одной стороны, является обобщением авторегрессионных моделей для многомерных временных рядов (временные ряды должны быть стационарными), а с другой – представляет собой систему одновременных уравнений в ее приведенной форме (эндогенные переменные выражены в явном виде через предопределенные). Особенность спецификации модели VAR состоит в том, что вектор предопределенных переменных не включает экзогенные переменные.
При моделировании VAR(p)-процессов спецификацию модели (1) обобщают следующим образом 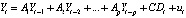[2]:
, (2)
где Ak – (m×m)-матрица коэффициентов, k = 1,..., p – величина лага, ut – m-мерный вектор процесса белого шума с (m×m)-ковариационной матрицей Ω, Dt – (M×1)-вектор столбец, включающий детерминированные регрессоры (которыми могут быть: константа, тренд, фиктивные переменные); C – (m×M)-матрица коэффициентов детерминированных регрессоров. Отсутствие автокорреляции вектора возмущений в модели VAR(p) значительно упрощает процедуру ее оценивания. Так как случайные возмущения уравнений представляют собой белый шум, который не коррелирует с прошлыми значениями уровней ряда, для оценки параметров модели VAR используется обычный метод наименьших квадратов (МНК), который последовательно применяется к каждому уравнению системы отдельно. Состоятельная оценка ковариационной матрицы случайных возмущений вычисляется через МНК-остатки отдельных уравнений, входящих в систему. В случае, если возмущение модели имеет нормальное распределение, для оценки параметров можно использовать условный метод максимального правдоподобия (ММП), алгоритм которого, как и алгоритм МНК, включен в современные эконометрические пакеты.
VAR(p)-модели в программной среде R
При построении моделей VAR(p) необходимо: 1) проверить временные ряды, включенные в вектор эндогенных переменных модели, на стационарность; 2) выбрать максимальную величину лага, учитываемую в спецификации. Для проверки на стационарность временного ряда широкое применение получил расширенный тест Дики–Фуллера ADF (Augmented Dickey–Fuller Test), реализованный во всех эконометрических пакетах. В тесте ADF предполагается, что нестационарность экономических данных объясняется их генерацией процессами случайного блуждания, случайного блуждания с дрейфом или комбинацией случайного блуждания с дрейфом и линейным временным трендом. В программной среде R расширенный тест Дики–Фуллера выполняется при помощи функции adf.test(x) пакета tseries с основным аргументом x – объект «временной ряд» [1].
Максимальная величина лага модели VAR(p) подбирается при помощи информационных критериев. Модель оценивается при различных значениях лага, и выбирается лаг, минимизирующий значение информационного критерия. Функция, реализующая процедуру выбора максимальной величины лага в программной среде, R – VARselect() пакета vars. Функция возвращает значения информационных критериев и ошибку прогноза для последовательного увеличения лага.
Для оценки модели VAR(p) и построения прогнозов в программной среде R используется функция VAR () пакета vars с основными параметрами: M – матрица, включающая значения эндогенных переменных модели; p – величина лага (по умолчанию равная единице), type – тип включения детерминированных регрессоров («const» – включение свободного члена, «trend» – включение тренда, «both» – включение свободного члена и тренда, «none» – модель без свободного члена и тренда), exogen – включение экзогенных переменных в спецификацию модели, ic – выбор информационного критерия для определения оптимальной величины максимального значения лага («AIC» – Акайке, «HQ» – Хеннона–Куина, «SC» – Шварца).
Прогнозирование VAR-модели выполняется после оценки ее параметров и диагностики предпосылок при помощи функции predict для объектов класса varest для периода упреждения, задаваемого параметром n.ahead, с вычислением доверительных интервалов, границы которых вычисляются для заданной доверительной вероятности (по умолчанию 0,95). Функция возвращает список из трех элементов – объектов класса varprd [2]:
fcst – список матриц, содержащих прогнозные значения, нижнюю и верхнюю границы в соответствии с выбранным доверительным интервалом, ci и его среднее значение; endog – матричный объект, содержащий эндогенные переменные; varest – объект, формируемый функцией VAR().
Графическое представление объектов класса varprd осуществляется при помощи функции fanchart(), которая позволяет пользователям задавать цвета и критические значения для построения доверительных интервалов.
VAR(p)-модель: оценка на основании эмпирических данных
Для построения модели VAR были использованы два макроэкономических показателя: расходы на конечное потребление (Y) и валовое накопление (X) в РФ. В табл. 1 приводятся годовые данные показателей за период с 1991 по 2019 гг. включительно (в млрд руб.) [3].
Таблица 1
Годовые значения макроэкономических показателей
Для проверки временных рядов на стационарность использовался расширенный тест Дики–Фуллера в программной среде R. Как и следовало ожидать, макроэкономические ряды Y и X нестационарны. Поэтому в качестве первичной обработки они были подвергнуты логарифмированию и вычислению разностей первого порядка. Преобразованные переменные y и x, практически показывающие процентное изменение динамики исходных показателей, являются стационарными и используются в качестве исходных переменных при построении модели VAR. Выбор величины лага модели VAR(p) выполнялся одновременно с тестированием предпосылок модели относительно случайного возмущения при помощи обобщенных тестов, применяемых для диагностики моделей многомерных временных рядов: теста Портманто (Portmanteau Test) на автокорреляцию, теста Бреуша–Годфри (Breusch–Godfrey) на гетероскедастичность, теста Харке–Бера (Jarque–Bera test) на нормальность распределения возмущений. Остатки модели VAR(1) оказались автокоррелированными, и к тому же стандартные ошибки модели VAR(1): sy = 0,198, sx = 0,248 больше стандартных ошибок модели VAR(2) sy = 0,098, sx = 0,204. Запишем спецификацию модели авторегрессии второго порядка VAR(2) с двумя переменными: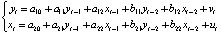
(3)и ее оцененную форму:
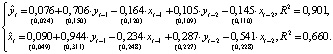(4)BVAR(p)-модель: оценка на основании эмпирических данныхМодели векторной авторегрессии являются моделями без ограничений на параметры, поэтому их основным недостатком служит перепараметризация, поскольку количество оцениваемых параметров быстро возрастает с увеличением числа переменных и величины лага, а как известно, для правильного отражения динамики фактических временных рядов требуется включение большого числа лагов [4]. Следует учесть и требование к увеличению выборки для оценки автоковариационной матрицы параметров [5]. Одним из следствий перепараметризации является рост дисперсий оценок параметров. Для решения этой проблемы рекомендуется контролировать количество параметров наложением на них общей структуры при помощи байесовских или эмпирических байесовских методов (Bayesian vector autoregression, BVAR).В моделях BVAR ограничения на параметры накладываются с учетом априорной информации о характере их распределения. Математическое ожидание параметра при эндогенной переменной с единичным лагом полагается равным единице. В соответствии со схемой назначения априорной информации для параметров модели VAR, предложенной Литтерманом, [6], [4]:1) параметры первого лага эндогенной переменной соответствуют параметрам авторегрессии первого порядка AR(1), параметры при остальных лаговых переменных приравниваются к нулю;2) стандартные ошибки параметров определяются через постоянные коэффициенты – гиперпараметры, назначаемые исследователем:λ1 – параметр регуляризации: при λ1 → 0 априорное распределение совпадает с апостериорным, исходные данные не оказывают влияния на оценку параметров; при λ1 → ∞ апостериорное математическое ожидание параметров сходится к МНК-оценке;λ2 – параметр кросс-регуляризации, добавляющий дополнительную жесткость лагам других переменных, включенных в уравнение. Значение λ2 < 1 показывает, что влияние лагов других переменных на прогноз эндогенной переменной меньше, чем ее собственных лагов;λ3 – отвечает за скорость убывания априорной дисперсии с увеличением лага. Стандартные ошибки параметров вычисляются по следующему правилу [6]:
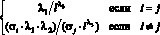, (5)где i – номер i-ой переменной в i-ом уравнении модели векторной авторегрессии, j – номер j-ой переменной в i-ом уравнении модели векторной авторегрессии, σi, σj – стандартные ошибки возмущений модели авторегрессии первого порядка AR(1), для i-ой и j-ой переменных соответственно. Продемонстрируем алгоритм задания априорных параметров распределения для модели векторной авторегрессии второго порядка VAR(2) с двумя переменными (3), с вектором параметров модели VAR(2), включающим следующие элементы:
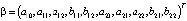. (6)Из обозначений (3) следует, что коэффициентом авторегрессионной модели первого порядка для переменной yt является параметр a11, для переменной xt является параметр a22, и, следовательно, в соответствии со схемой назначения априорной информации для параметров модели VAR, предложенной Литтерманом, вектор априорных математических ожиданий параметров модели будет иметь вид:
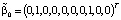. (7)Диагональные элементы матрицы H априорных дисперсий параметров (6) определяются по правилу (5). В табл. 2 приведены формулы для вычисления средних квадратических отклонений параметров (ско).
Таблица 2
Средние квадратические отклонения параметров модели
|
№ |
Год |
Y |
X |
№ |
Год |
Y |
X |
|
1 |
1991 |
0,9 |
0,5 |
16 |
2006 |
17809,7 |
5698,8 |
|
2 |
1992 |
9,2 |
6,6 |
17 |
2007 |
21968,6 |
8034,1 |
|
3 |
1993 |
106,8 |
46,3 |
18 |
2008 |
27543,5 |
10526,1 |
|
4 |
1994 |
422,1 |
156 |
19 |
2009 |
29269,6 |
7344,8 |
|
5 |
1995 |
1016,6 |
363,4 |
20 |
2010 |
32514,6 |
10472,7 |
|
6 |
1996 |
1435,9 |
475,2 |
21 |
2011 |
40883,8 |
14584,1 |
|
7 |
1997 |
1776,1 |
514,8 |
22 |
2012 |
47273,4 |
16721,9 |
|
8 |
1998 |
2003,8 |
393,5 |
23 |
2013 |
52433,6 |
16985 |
|
9 |
1999 |
3285,7 |
715,3 |
24 |
2014 |
56735,9 |
17695,5 |
|
10 |
2000 |
4476,8 |
1365,7 |
25 |
2015 |
58531,1 |
18402,8 |
|
11 |
2001 |
5886,8 |
1963,1 |
26 |
2016 |
61398,5 |
19773,4 |
|
12 |
2002 |
7484,1 |
2169,3 |
27 |
2017 |
65289,5 |
21681,2 |
|
13 |
2003 |
9058,7 |
2755,1 |
28 |
2018 |
70147,5 |
22996,2 |
|
14 |
2004 |
11477,9 |
3558,9 |
29 |
2019 |
75578,5 |
25427,6 |
|
15 |
2005 |
14438,2 |
4338,7 |
|
Параметры |
a10 |
a11 |
a12 |
b11 |
b12 |
|
ско |
|
|
|
|
|
|
Параметры |
a20 |
a21 |
a22 |
b21 |
b22 |
|
ско |
|
|
|
|
|
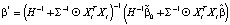, (8)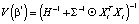
, (9)где β* – вектор апостериорных математических ожиданий параметров модели VAR(2) с двумя переменными, Xt – матрица исходных временных рядов, 
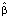– вектор МНК-оценок параметров, 
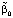– вектор априорных математических ожиданий параметров модели, Σ – матрица с единицами на главной диагонали, H – диагональная матрица с априорными дисперсиями параметров модели. Ниже приводятся результаты оценивания модели алгоритма (8), (9) с гиперпараметрами: λ1 = 0,7, λ2 = 1, λ3 = 2.
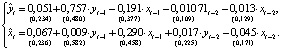(10)Стандартные ошибки модели BVAR(2) (sy = 0,124; sx = 0,272) больше стандартных ошибок модели VAR(2) (sy = 0,098; sx = 0,204). Оценки параметров и их дисперсий существенно зависят от значений гиперпараметров.Точечную и интервальную оценку параметров регрессионной модели байесовским методом в программной среде R можно выполнить при помощи функции MCMCregress пакета MCMCpack: MCMCregress(formula, data, b0=b0,B0=B0), с основными параметрами: formula – спецификация регрессионной модели; data – данные в форме data.frame; b0 – априорное среднее значение вектора параметров; B0 – априорное значение автоковариационной матрицы оценок параметров [7]. Ниже приводятся результаты оценивания модели (3) по данным табл. 1 при помощи функции MCMCregress с начальными значениями вектора параметров (7) и оценкой автоковариационной матрицы H:
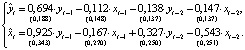(11)ВыводыОценки параметров моделей (4) и (11) отличаются незначительно, однако стандартные ошибки модели BVAR(2), оцененные в рамках метода MCMC, sy = 0,005, sx = 0,017, значительно меньше стандартных ошибок BVAR(2), оцененных при помощи алгоритмов (8), (9) и модели BVAR(2). Этот результат подтверждается многочисленными исследованиями в области количественной оценки воздействия внутренних и внешних факторов при моделировании макроэкономических процессов [8].