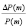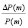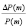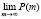Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Как известно, купонная облигация – один из наиболее распространенных инструментов для инвестиций с фиксированным доходом. Основными параметрами, влияющими на оценку облигации, являются: срок до погашения, купонная ставка и доходность к погашению облигации [1–3]. В ряде работ, например [4–6], приведены математические доказательства влияния основных параметров облигации на ее инвестиционные свойства, прежде всего на поведение цены и ее процентного изменения при изменении одного из основных параметров. Такой параметр, как число купонных платежей в году, к основным не относится. В связи с этим, очевидно, в литературе достаточно мало сообщений об этом параметре, вследствие чего теория финансовых инвестиций с фиксированным доходом представляется неполной. В некоторых работах встречаются короткие упоминания о влиянии данного параметра на инвестиционные свойства облигации [4, 7]. О влиянии частоты выплаты купонного дохода сообщают некоторые интернет-ресурсы. Например, [8]: «Большую ценность имеют бумаги, ставка по которым выплачивается чаще».

В работах автора данной статьи [9–11] рассмотрены задачи о влиянии числа купонных платежей в году на цену, дюрацию и доходность инвестиции в облигацию. Результаты получены на основе принятой на многих рынках формулы для цены облигации, в которой доходность к погашению рассматривается как годовая номинальная процентная ставка [2, с. 908]. Результаты работ [10, 11] имеют экономическое объяснение и подтверждаются рыночными наблюдениями, чего нельзя сказать о результатах работы [9], посвященной влиянию параметра на цену облигации. В связи с этим было предложено рассмотреть существующие подходы к определению доходности к погашению облигации.

Как известно, цена облигации равна приведенной стоимости потока платежей по облигации. Для приведения членов потока необходима соответствующая данной облигации доходность к погашению. Смысл этого показателя раскрывается в других его названиях: заявленная доходность, преобладающая рыночная процентная ставка соответствующего сегмента рынка [1], требуемая доходность [2]. На многих рынках для дисконтирования членов денежного потока применяется годовая номинальная процентная ставка r(m), где m – число купонных платежей в году [2, с. 477, 908; 12, с. 13]. Как правило, периодичность сложного процента соответствует периодичности платежей [12, с. 13]. Основу такого подхода заложил американский закон о справедливом кредитовании [3, с. 127], который был введен «для уменьшения проблем» участников рынка. Как видим, подход к определению доходности к погашению как годовой номинальной процентной ставки является формальным, существующим как рыночное соглашение между участниками рынка. «Если платежи поступают раз в полгода, на рынке принято соглашение использовать 1/2 годовой процентной ставки» для дисконтирования членов денежного потока [2, с. 477].

Другой вид доходности к погашению – годовая эффективная ставка r [2, с. 486; 12, с. 13], связанная со ставкой r(m) соотношением

.

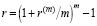В работе [13, с. 62] автор подчеркивает, что ставка r(m) как годовая ставка доходности облигации является приближенной, а r – это точная годовая доходность.

По определению эффективной ставки, r – это ставка сложных процентов, начисляемых один раз в году, эквивалентная ставке r(m). Ставка r показывает годовую доходность инвестиции в облигацию при условии владения облигацией до момента погашения и реинвестировании купонных платежей по ставке доходности в момент покупки r(m) (можно посмотреть в [11]). Таким образом, ставка r для дисконтирования членов денежного потока по облигации может быть использована в тех случаях, когда инвестор исходит из оценки эффективности инвестиции в облигацию (требуемого значения доходности инвестиции).

В статье [9] для изучения зависимости цены облигации от числа купонных платежей в году m была использована формула, в которой доходность к погашению определена как номинальная процентная ставка r(m):

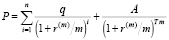. (1)

Это формула для котируемой цены облигации, когда до погашения остается целое число купонных периодов (Т лет – срок до погашения облигации, А – номинал облигации, 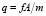– размер купонного платежа, f – годовая купонная ставка). Формула (1) преобразуется к виду

.

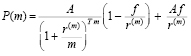На основе данной формулы при фиксированных значениях T, f и r(m) доказаны утверждения: котируемая цена облигации, продающейся с премией, увеличивается с увеличением числа купонных платежей в году, а котируемая цена облигации, продающейся с дисконтом, уменьшается с увеличением числа купонных платежей в году.

Приведенные в работе [9] вычисления цены облигации по формуле (1) для различных значений m подтверждают справедливость доказанных утверждений. Однако попытки объяснить полученные утверждения не привели к приемлемому результату. Если поведение цены облигации, продающейся с премией, можно объяснить ростом спроса на такие облигации с увеличением числа купонных платежей в году, то поведение цены облигации, продающейся с дисконтом, а именно – ее уменьшение с увеличением числа купонных платежей в году, объяснить не представляется возможным. Кроме того, из (1) следует, что при f = r(m) цена облигации, продающейся по номиналу, не зависит от числа купонных платежей в году и остается равной номиналу облигации, что не соответствует сообщению интернет-ресурса, приведенному в начале статьи. Таким образом, задача о зависимости цены облигации от числа купонных платежей в году требовала дальнейшего рассмотрения.

Как уже отмечалось, значение показателя r(m) как годовой ставки доходности облигации автор работы [13, с. 62] называет приближенным, а использование ставки дисконтирования в виде r(m)/m в формуле (1) не вполне корректным [13, с. 39]. В связи с этим можно предположить, что и значения цен, полученные по формуле (1), являются не вполне корректными.

Целью данной работы является исследование зависимости цены облигации от числа купонных платежей в году на основе формулы для цены облигации, в которой доходность к погашению рассматривается как годовая эффективная процентная ставка r:

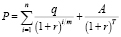. (2)

Материалы и методы исследования

Для решения задачи применяются методы дифференциального исчисления и теории рядов. Формула (2) преобразуется к виду

, ,

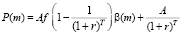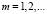где .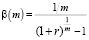

Предельное значение функции P(m):

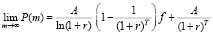. (3)

Для изучения зависимости P(m) используем вспомогательную функцию:

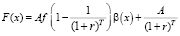, x ≥ 1, (4)

где .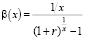

Функция F(x) и цена P(m) связаны соотношением

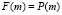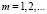, где . (5)

Очевидно, что свойства функции F(x) определяются свойствами функции β(x). Докажем лемму.

Лемма. Функция β(x) является возрастающей и вогнутой на множестве x ≥ 1.

Доказательство. Рассмотрим функцию 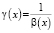, x ≥ 1.

Тогда

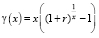, x ≥ 1.

Функцию γ(x) разложим в степенной ряд. Так как

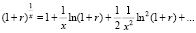, x ≥ 1,

то

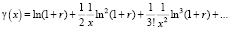, x ≥ 1.

Тогда

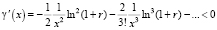, x ≥ 1,

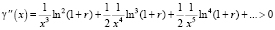, x ≥ 1.

Таким образом, 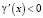, , 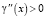где x ≥ 1.

Так как 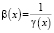, то 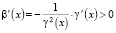, x ≥ 1,

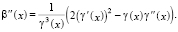
Чтобы определить знак второй производной 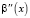на множестве x ≥ 1, разложим функцию 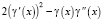в степенной ряд, используя правило перемножения рядов [14, с. 320]. Получим

.

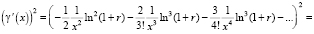
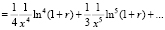Тогда

.

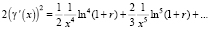Так как

,

,

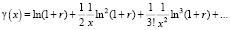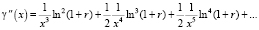то для произведения функций 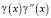получим

.

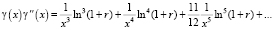Тогда

, .

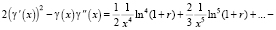
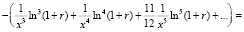
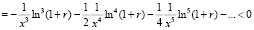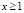Отсюда 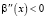, 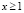. Таким образом, для функции β(x) имеем

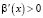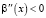, , x ≥ 1. Лемма доказана.

Теорема 1. При заданных значениях T, f и r последовательность {P(m)} является возрастающей.

Доказательство. Из равенства (4) и леммы следует, что

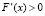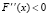, , x ≥ 1 -

функция F(x) является возрастающей и вогнутой на множестве x ≥ 1. Тогда

, .

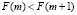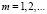Согласно равенству (5), 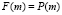, 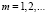. Тогда получим

,

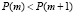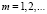
- последовательность {P(m)} является возрастающей. Подчеркнем, что этот результат не зависит от купонной ставки. Теорема доказана.

Следующая теорема посвящена поведению скорости роста цены облигации с увеличением параметра m. Предположим, число купонных платежей в году увеличилось с m до (m + 1) при фиксированных значениях остальных параметров облигации. В силу теоремы 1 цена облигации увеличится на величину 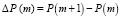, а скорость роста цены характеризуется отношением 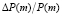. Заметим, что 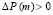и .

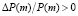Теорема 2. При заданных T, f и r чем больше m, тем меньше абсолютный и относительный рост цены облигации при увеличении числа купонных платежей в году на 1.

Доказательство. Докажем утверждение теоремы для абсолютного изменения цены облигации при увеличении числа купонных платежей в году на 1, с m до (m + 1). Вследствие равенства (5)

.

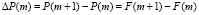Для функции F(x) на отрезке 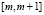выполняется теорема Лагранжа. Тогда существует 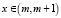, при котором выполняется равенство:

.

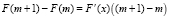Из двух последних равенств следует, что

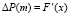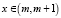, . (6)

Пусть 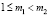. Вследствие равенства (6)

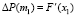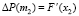, , (7)

где 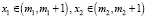. Так как 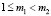, то .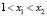

Поскольку вторая производная 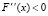, x ≥ 1, то первая производная F'(x) – убывающая функция на множестве x ≥ 1. Тогда

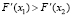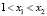, где . (8)

Из (7) и (8) получим

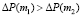, где .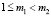

Утверждение теоремы для абсолютного роста цены облигации доказано.

Для относительного роста цены выполняется неравенство

, ,

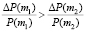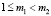поскольку 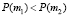при 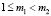по теореме 1 и 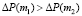по уже доказанному. Теорема доказана. Заметим, что утверждения теоремы 2 не зависят от купонной ставки, как и теоремы 1.

Результаты исследования и их обсуждение

В таблице приводятся примеры вычислений членов последовательностей {P(m)} по формуле (2) и последовательностей {ΔP(m)} и {ΔP(m)/P(m)} для облигаций, продающихся с дисконтом, по номиналу, с премией. Вычисления выполнены для гипотетических облигаций с параметрами A = 100, T = 5 лет, r = 0,08. Значения пределов 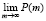вычислены по формуле (3). Как видим, результаты вычислений подтверждают доказанные утверждения теорем 1 и 2: при любых соотношениях между ставками f и r последовательность {P(m)} является возрастающей, а последовательности {ΔP(m)} и {ΔP(m)/P(m)} – убывающими.

Таким образом, на основании формулы (2) при фиксированных значениях T, f и r, где r – годовая эффективная ставка доходности, установлено, что с увеличением параметра m цена купонной облигации увеличивается. При этом абсолютный и относительный рост цены облигации при увеличении параметра m на 1 уменьшаются, что говорит об уменьшении скорости роста цены с увеличением m. Рост цены облигации с увеличением параметра m при любой купонной ставке, по нашему мнению, означает рост спроса на облигации при увеличении параметра m. Предположение о росте спроса на облигации с увеличением параметра m соответствует результатам работ [10] и [11]. Один из выводов в работе [10] – рост привлекательности инвестирования в облигации при увеличении числа купонных платежей в году в связи с уменьшением «среднего срока», т.е. дюрации облигации. Аналогичный вывод и в работе [11], в которой установлено, что с увеличением числа купонных платежей в году доходность инвестиции в облигацию увеличивается при любой купонной ставке и любой ставке реинвестирования платежей от облигации.

Зависимость цены P(m), величин ΔP(m) и ΔP(m)/P(m) от параметра m для различных соотношений между f и r

Как видим, результаты данной работы, полученные по формуле (2), согласуются с другими исследованиями и сообщениями интернет-ресурсов (одно из сообщений приведено в начале статьи).

Заключение

По нашему мнению, отличия результатов исследований зависимости цены облигации от числа купонных платежей в году по формулам (1) и (2) обусловлены различием двух подходов к определению доходности к погашению облигации. Формула (1) предложена на основе рыночного соглашения, имеющего формальный характер. Как показали результаты работы [9], для данного исследования номинальная ставка доходности r(m) является не вполне корректным приближением доходности к погашению. В то время как доходность облигации в виде годовой эффективной процентной ставки r является более точной и измеряет эффективность инвестиции в облигацию.

Результаты работы могут быть полезны как эмитенту облигаций при конструировании параметров облигации, так и инвестору при принятии инвестиционных решений.