Система коммерческих банков представляет собой эволюционирующий и динамичный системный объект. Изменение системы коммерческих банков в процессе эволюции предполагает два варианта развития событий: либо редукция и деградация системы, либо прогресс и развитие. Ситуация, когда эволюционный процесс благоприятствует системному развитию, свидетельствует о прогрессе системы. Однако эволюционный процесс может привести и к деградации системы, краху системообразующих банков и затяжному финансовому кризису. В этой связи проблема раннего обнаружения деструктивных явлений, развивающихся внутри банковского сектора, тесно связана с решением задачи системной диагностики. Достаточным и необходимым результатом разрешения данной проблемы представляется получение достоверной оценки о состоянии системы коммерческих банков в конечный момент времени и определение тенденций, связанных с изменением состояния за период времени. Достижение подобного результата возможно в рамках решения диагностической задачи. Инструментом решения будет выступать диагностическая модель системы коммерческих банков.
Чем выше уровень эволюционного развития системы коммерческих банков, тем большим разнообразием характеризуются межэлементные связи внутренней системной среды и связи с внешней средой. Снижение тесноты и эффективности внутренних и внешних связей банковского сектора ведет к возникновению кризисных явлений и деструктивных процессов. Современный системный подход и общая теория систем в качестве количественной меры тесноты и эффективности взаимодействия системных элементов рассматривает информацию. Таким образом, информацию можно считать одновременно и количественной мерой системного регресса либо прогресса. Формализация информационного критерия в рамках диагностической задачи находит свое отражение в энтропийном моделировании.
В процессе анализа научных разработок, посвященных применению энтропийного подхода для оценки состояния банковского сектора, были изучены следующие исследования. Так, в своей работе [1] М. Тойванен, применяя вычисления на основе энтропийных моделей, оценивает риски реализации и распространения масштабного банковского кризиса в Финляндии в 2005–2007 гг. Автор в своем исследовании базировался на закономерностях и трендах, характерных для банковского кризиса в Финляндии 1990-х. Что касается среды распространения кризиса, то автор в качестве такой среды рассматривал рынок межбанковского капитала. Джианпинг Ли с коллегами в своей работе [2] формулируют энтропийную модель, базирующуюся на статистической информации фондового рынка. С помощью предложенной модели авторами определяется теснота и характер взаимозависимости китайских банков и прогнозируется механизм реализации системных рисков в китайской банковской системе. Моника Биллио с соавторами [3], объединив энтропийное моделирование и методику VAR, предложили собственный подход к оценке и прогнозированию системного риска банковского сектора на основе расчета энтропийных показателей. По итогам анализа представленных работ можно констатировать слабую разработанность изучаемой проблемы и отсутствие достаточно простых и адекватных экономико-математических моделей, позволяющих связать инструментарий энтропийного подхода с фактическими количественными параметрами состояний банковской системы.
Цель исследования: решение диагностической задачи по поводу оценки финансового состояния банковского сектора РФ с помощью энтропийного моделирования.
Теоретические аспекты и методы исследования
Сформулируем математическую модель банковского сектора РФ в виде многомерной случайной величины X = (X1,X2,…Xm). В рамках предложенной модели сделаем допущение, что каждая составляющая Xi вектора X является одномерной случайной величиной, характеризующей определенный аспект функционирования банковской системы. Подобные векторные компоненты могут как коррелировать друг с другом, так и являться независимыми. Их дисперсии следует рассматривать в качестве характеристик интенсивности и тесноты связи рассматриваемой системы с внешней средой, а индексы детерминации – в качестве характеристик межэлементных связей внутренней среды. Иными словами, данные показатели характеризуют такие системные свойства, как аддитивность и целостность. Однако возникает вопрос о связи энтропии и указанных показателей.
Развивая подход К. Шеннона [4], Тырсин и Лебедева-Ворфоломеева в своих работах [5; 6] обосновывают возможность оценки энтропии стохастической системы с учетом двух энтропийных показателей, характеризующих такие системные свойства, как аддитивность и целостность.
Предположим, что существуют две системы непрерывных случайных величин 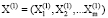 и X(2) =
и X(2) = 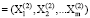 , каждая из которых соответствует предыдущему и текущему периодам функционирования банковского сектора. Что касается соответствующих составляющих обеих системы непрерывных случайных величин
, каждая из которых соответствует предыдущему и текущему периодам функционирования банковского сектора. Что касается соответствующих составляющих обеих системы непрерывных случайных величин 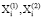 (i = 1,2,...,m), то они имеют конечные дисперсии и описываются однотипными распределениями с некоторыми параметрами положения и масштаба. Тогда, по Тырсину и Лебедевой-Ворфоломеевой, разность энтропий указанных систем случайных величин определяется формулой 1:
(i = 1,2,...,m), то они имеют конечные дисперсии и описываются однотипными распределениями с некоторыми параметрами положения и масштаба. Тогда, по Тырсину и Лебедевой-Ворфоломеевой, разность энтропий указанных систем случайных величин определяется формулой 1:
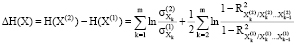 , (1)
, (1)
где 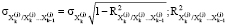 – индексы детерминации соответствующих регрессионных зависимостей (k = 2,3,…, m; j = 1,2) [5].
– индексы детерминации соответствующих регрессионных зависимостей (k = 2,3,…, m; j = 1,2) [5].
В случаях, когда гауссовский вектор X = (X1, X2, X3…Xm) характеризуется совместным нормальным распределением с корреляционной матрицей RX, корреляционные связи между его компонентами определяются зависимостью линейного типа, а индекс детерминации 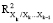 рассчитывается по формуле 2:
рассчитывается по формуле 2:
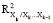 = 1 –
= 1 – 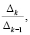 (2)
(2)
где Δk – угловые миноры корреляционной матрицы RX; k = 1,2,…m [6].
Тырсин и Ворфоломеева-Лебедева подвергают формулу 2 интерпретации и определяют формулы по расчету энтропийных показателей (формула 3). Первое слагаемое H(X)∑ условно именуется приростом энтропии хаотичности (формула 4). Оно определяет изменение энтропии при росте (уменьшении) независимости элементов системы. Второе слагаемое H(X)R следует рассматривать в качестве прироста энтропии системной самоорганизации (формула 5). Данная величина отражает изменение энтропии при росте (уменьшении) совместной корреляционной взаимосвязи между элементами системы [5].
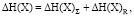 (3)
(3)
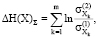 (4)
(4)
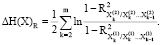 (5)
(5)
Сформируем систему сводных факторов, пригодную для энтропийного моделирования. Использование предложенной в работах Тырсина и Ворфоломеевой-Лебедевой энтропийной модели возможно в том случае, если для системы групповых сводных факторов X1,..., Xm в виде случайного вектора X выполняется закон нормального распределения. Введем следующие исходные переменные, характеризующие состояние системы коммерческих банков РФ в период с 2012 г. по 2019 г.: x1 – месячный темп прироста активов банковского сектора, %; x2 – месячный темп прироста собственных средств (капитала), %; x3 – месячный темп прироста кредитов и прочих размещенных средств, предоставленных нефинансовым организациям, %; x4 – месячный темп прироста вкладов физических лиц, %. Источником указанных показателей выступают Обзоры банковского сектора Российской Федерации, регулярно публикуемые Центральным банком России на официальном сайте cbr.ru [7]. Выбор факторов был обусловлен тем, что отобранные показатели характеризуют основные финансовые фонды системы коммерческих банков: фонд финансовых ресурсов, привлеченных в виде вкладов физических лиц; фонд собственных средств (капитала); ссудный фонд, ориентированный на нефинансовые организации; фонд активов. Темп прироста характеризует динамику того или иного фонда за единицу времени. Синхронность изменения показателей свидетельствует о слаженном функционировании элементов системы коммерческих банков и о нормальной работе перераспределительного механизма системы, несинхронное изменение говорит о возможной дестабилизации системы.
На основе динамических рядов месячных значений подобранных показателей была сформирована матрица исходных данных. Энтропийное моделирование проведем на базе полученной системы групповых сводных факторов X1, X2, X3, X4 в виде вектора X = (X1, X2, X3, X4). Для данных вектора X характерно нормальное распределение. Для повышения точности модели был укрупнен временной период, описывающий стационарное состояние банковской системы, с месячного до двухгодового: период 1 включает интервал 2012–2013 гг.; период 2 – интервал 2014–2015 гг.; период 3 – 2016–2017 гг.; период 4 – 2018–2019 гг. С помощью программы SPSS 17.0 были рассчитаны ковариационные и корреляционные матрицы для каждого вектора, соответствующего двухлетнему периоду:





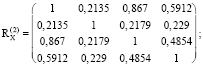


Далее приводится подробный механизм расчета изменения энтропийных показателей для периода 1 и периода 2. На основе данных ковариационных матриц Σ(1) (2012–2013 гг.) и Σ(2) (2014–2015 гг.) было найдено изменение показателя энтропии хаотичности:
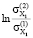 =
= 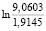 = 1,5544;
= 1,5544; 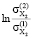 =
= 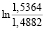 = 0,0319;
= 0,0319; 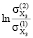 =
= 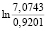 = 2,0397;
= 2,0397;
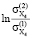 =
= 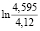 = 0,1091;
= 0,1091; 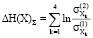 = 1,5544 + 0,0319 + 2,0397 + 0,1091 =≈ 3,74.
= 1,5544 + 0,0319 + 2,0397 + 0,1091 =≈ 3,74.
С учетом данных корреляционных матриц 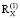 (2012–2013 гг.) и
(2012–2013 гг.) и 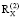 (2014–2015 гг.) было вычислено изменение показателя энтропии системной самоорганизации:
(2014–2015 гг.) было вычислено изменение показателя энтропии системной самоорганизации:
0,5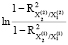 = 0,5
= 0,5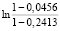 = 0,1147;
= 0,1147;
0,5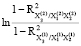 = 0,5
= 0,5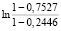 = -0,5583;
= -0,5583;
0,5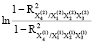 = 0,5
= 0,5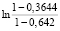 = 0,287;
= 0,287;
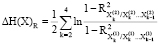 =≈ – 0,16.
=≈ – 0,16.
Было рассчитано изменение энтропии между первым и вторым аналитическим периодом: 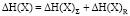 = 3,74 + (- 0,16) = 3,58.
= 3,74 + (- 0,16) = 3,58.
Используя данные ковариационных матриц ∑(2) (2014–2015 гг.) и ∑(3) (2016–2017 гг.), было определено изменение показателя энтропии хаотичности для периодов 2 и 3:
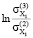 =
= 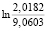 = -1,5017;
= -1,5017; 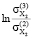 =
= 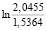 = 0,2862;
= 0,2862; 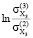 =
= 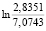 = -0,9144;
= -0,9144;
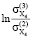 =
= 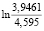 = -0,1522;
= -0,1522; 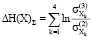 = -1,5017 + 0,2862 – 0,9144 – 0,1522 =≈ -2,28.
= -1,5017 + 0,2862 – 0,9144 – 0,1522 =≈ -2,28.
Основываясь на данных корреляционных матриц 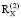 (2014–2015 гг.) и
(2014–2015 гг.) и 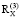 (2016–2017 гг.), нашли изменение показателя энтропии системной самоорганизации:
(2016–2017 гг.), нашли изменение показателя энтропии системной самоорганизации:
0,5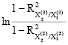 = 0,5
= 0,5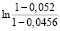 = -0,0034;
= -0,0034;
0,5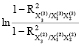 = 0,5
= 0,5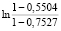 = 0,2988;
= 0,2988;
0,5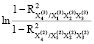 = 0,5
= 0,5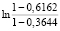 = -0,2522;
= -0,2522;
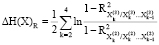 =≈ 0,04.
=≈ 0,04.
Определим изменение энтропии между вторым и третьим аналитическим периодом: 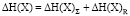 = -2,28 + 0,04 = -2,24.
= -2,28 + 0,04 = -2,24.
На основе данных ковариационных матриц ∑(3) (2016–2017 гг.) и Σ(4) (2018–2019 гг.) было найдено изменение показателя энтропии хаотичности:
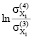 =
= 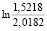 = -0,2823;
= -0,2823; 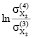 =
= 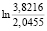 = 0,625;
= 0,625; 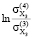 =
= 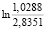 = -1,0136;
= -1,0136;
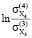 =
= 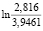 = -0,3374;
= -0,3374; 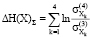 = -0,2823 + 0,625 – 1,0136-0,3374 =≈ -1,01.
= -0,2823 + 0,625 – 1,0136-0,3374 =≈ -1,01.
Данные корреляционных матриц 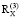 (2016–2017 гг.) и
(2016–2017 гг.) и 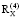 (2018–2019 гг.) были использованы при вычислении изменения показателя энтропии системной самоорганизации:
(2018–2019 гг.) были использованы при вычислении изменения показателя энтропии системной самоорганизации:
0,5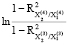 = 0,5
= 0,5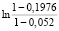 = -0,0834;
= -0,0834;
0,5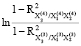 = 0,5
= 0,5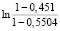 = 0,1;
= 0,1;
0,5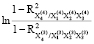 = 0,5
= 0,5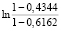 = 0,194;
= 0,194;
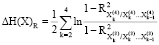 =≈ 0,21.
=≈ 0,21.
Было рассчитано изменение энтропии между третьим и четвертым аналитическим периодом: ΔH(X) = ΔH(X)∑ + ΔH(X)R = -1,01 + 0,21 = -0,8.
Результаты исследования и их обсуждение
Результаты расчетов изменения параметра системной энтропии банковского сектора России по всем периодам представлены в таблице.
Результаты оценки изменения энтропии банковского сектора для двухгодичных временных интервалов с 2012 по 2019 г.
|
Диапазон периодов |
1-2 |
2-3 |
3-4 |
|
ΔH(X)∑ |
3,74 |
-2,28 |
-1,01 |
|
ΔH(X)R |
-0,16 |
0,04 |
0,21 |
|
ΔH(X) |
3,58 |
-2,24 |
-0,8 |
Локальный максимум изменения энтропийного критерия наблюдается в 2014–2015 гг. после двухлетнего периода 2012–2013 гг. Достижение подобного показателя явилось результатом роста системной хаотичности (неблагоприятные тенденции во внешней среде) и уменьшением системной взаимозависимости элементов банковского сектора (негативные процессы внутри системы коммерческих банков). Именно на конец 2014 г. приходится развитие российского экономического кризиса, порожденного экономическими санкциями со стороны ряда стран. В 2016–2017 гг. по сравнению с предыдущим двухгодичным периодом уменьшение системной энтропии оценивается в (-2,24) условной единицы, а в 2018–2019 гг. – в (-0,8) условной единицы. Полученные с помощью модели данные иллюстрируют преодоление банковским сектором России финансового кризиса к 2016–2017 гг. Достижение подобного результата стало следствием оздоровления банковского сектора России и поддержки со стороны государства. Для периода 2018–2019 гг. модель демонстрирует позитивное развитие банковского сектора, однако темп уменьшения системной энтропии (ΔH(X)R) сокращается, что свидетельствует о зарождении негативных процессов, способных привести к кризису системы.
Выводы
На основе методики энтропийного моделирования была сформулирована модель, которая позволила рассчитать показатель системной энтропии банковского сектора России – энтропийный критерий. В результате анализа полученных данных были выявлены периоды, для которых было характерно увеличение показателя системной энтропии и периоды, для которых демонстрировалось снижение данного показателя. Динамика изменения энтропийного критерия соответствует основным стадиям изменения банковской системы РФ в кризисный и посткризисный периоды. Это свидетельствует о возможности использования модели для решения задачи диагностики российского банковского сектора.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-010-00909.



