Механизм государственно-частного партнерства получил большое распространение за счет эффективности в вопросах модернизации инфраструктуры. Государственно-частное партнерство является приоритетным направлением экономического развития многих стран, в том числе и Российской Федерации, на это влияют три основные причины. Во-первых, каждое государство стремится к повышению эффективности, технологическим инновациям и повышению управленческого потенциала. Во-вторых, структура государственно-частного партнерства позволяет государству перекладывать определенные риски на частную сторону, с которыми частный сектор мог бы справиться лучше, тем самым уравновешивая риски и выгоды для государственного и частного секторов. В-третьих, механизм ГЧП соответствует стратегическому обязательству правительства многих стран в использовании частных инвестиций и партнерских отношений для достижения целей экономического роста страны.
В то же время проекты государственно-частного партнерства отличаются определенной сложностью, в большей степени это связано с системой оценивания рисков на этапе планирования. Поскольку стремительно развивающаяся глобализация, касающаяся преимущественно экономической сферы, становится причиной усложнения современных финансовых и социально-организационных систем, возрастает процент неустойчивости и неопределенности этих систем. В связи с этим является актуальным изучение механизмов регулирования чувствительности к событиям риска и ограничений, вызванных рисками потерь.
Проблемами оценивания рисков при форме государственно-частного партнерства занимались Т.А. Вивчар, К.П. Кривенок, А.А. Мацак, И.А. Мурашко, Н.Н. Семенова и др.
Исследования Т.А. Вивчар и К.П. Кривенок посвящены рациональному распределению рисков проектов ГЧП, авторами также выделен ряд проблем, возникающих на этапе идентификации и распределения рисков [1]. В одном из исследований приводится ряд рекомендаций для их рационального распределения [1].
В работах А.А. Мацака анализируется мировой опыт внедрения инноваций в области проектов ГЧП, также приводится ряд разработок наиболее эффективных стратегий для управления рисками при взаимодействии государства с частным сектором [2].
В работах Н.Н. Семеновой и др. рассматриваются основные подходы к оценке рисков в государственно-частном партнерстве [3]. В одной из работ приводится доказательство положения о том, что в настоящее время на территории РФ отсутствуют единая сложившаяся практика и единые определенные способы осуществления анализа рисков проектов ГЧП [4].
Предыдущими авторами, рассматривающими оценивание и распределение рисков в проектах ГЧП в качестве области научного знания, ранее не были представлены методы, способные констатировать и определять неизвестные величины, что наиболее характерно для такого понятия, как риск.
Цель исследования: обосновать эффективность байесовского подхода в оценке рисков проектов государственно-частного партнерства.
Материалы и методы исследования
В статье описаны возможности использования байесовского подхода при оценке рисков проектов государственно-частного партнерства. Методологической основой исследования послужили методы сравнительного анализа источников по исследуемой теме, формализации, синтеза и математического моделирования. Источниковая база исследования представлена современными отечественными исследованиями рассматриваемого вопроса.
Результаты исследования и их обсуждение
Нормативно-правовые основы регулирования ГЧП указывают на один из основополагающих признаков реализации проектов в области инфраструктуры – механизм распределения рисков между сторонами, представляющими как государство, так и частный сектор [5, с. 208].
Государственно-частное партнерство – это понятие, охватывающее широкий спектр форм сотрудничества между государственным и частным секторами, что определило в международной литературе и практике отсутствие единого общепринятого мнения о том, что представляет собой это партнерство. Однако общим во всех доводах является то, что решение о запуске проекта в рамках государственно-частного партнерства должно приниматься на основе анализа всех существующих рисков в рамках государственно-частного партнерства.
Применение механизма государственно-частного партнерства является многоаспектным решением. При рассмотрении данного способа взаимодействия государства с бизнесом возникает большое количество спорных моментов относительно того, сколько тех или иных административных услуг можно передать на аутсорсинг, какие из государственных услуг должны исполняться частной и публичной сторонами. При принятии этих решений государственно-частное партнерство не должно рассматриваться как универсальный метод, способный решить любую проблему. Применение механизма ГЧП должно анализироваться с точки зрения связанных с этим выгод и рисков. Одним из основных мотивов, который считается преимуществом использования государственно-частного партнерства, является привлечение частных инвестиций в области, традиционно считающиеся государственными, что особенно важно, поскольку большинство государств сталкиваются как на центральном, так и на местном уровнях с бюджетными ограничениями.
В данном исследовании в качестве ранее не изученного в этой области метода авторами предлагается решить проблему оценивания рисков с применением байесовского подхода в данном вопросе. Байесовские методы были реализованы посредством решения проблемы определения статистического описания различных процессов [6; с. 29]. Рассматриваемый подход обеспечивает использование наиболее распространённого математического инструментария для расчета распределения интересующего количества с учетом наблюдаемых данных (измерений) [7].
Суть байесовского подхода сводится к принципиально новому подходу в оценивании неизвестных коэффициентов, в рамках которого становится возможным изучить такие важные для построения прогнозов и анализа на предприятии эконометрические методы, как классическая регрессия, медианная регрессия, а также модели временных рядов [8, с. 5].
Возможность оценивания неизвестных коэффициентов обуславливается важным параметром байесовской теории – наличием априорной и апостериорной вероятностей.
Априорная вероятность – вероятность, присвоенная событию при отсутствии знания, поддерживающего его наступление [9].
Апостериорная вероятность – условная вероятность события при некотором условии, рассматриваемая в противоположность его априорной вероятности [9].
Апостериорная плотность вероятности основана на уже имеющихся наблюдениях (данных), а также на всех имеющихся контекстуальных знаниях и ограничениях. Стоит также отметить, что метод основан на подходе пространства состояний к моделированию временных рядов.
Таким образом, вследствие отличия байесовской методологии от других тем, что еще до получения данных становится возможным определить вероятность того или иного процесса, представленную математической моделью, целесообразно использование байесовского подхода в эконометрическом анализе рисков проектов ГЧП. Это объясняется, прежде всего, тем, что организации, существующие в рамках сотрудничества государства с бизнесом, испытывают сложности с анализом и прогнозированием стратегии предприятия, а также наиболее подвержены индивидуальным рискам ввиду того, что механизм распределения рисков осуществляется между сторонами ГЧП.
Рассмотрим целесообразность применения байесовского подхода в оценке риска на этапе планирования проекта ГЧП на примере простой задачи. Стоит отметить, что байесовский метод предполагает статистический расчет на модели, которая является скорее детерминированной, чем вероятностной. Также при решении следует ожидать, что полученные результаты будут являться случайной вариацией, взятой из некоторого базового распределения, которое задается посредством определения некоторых условий [10, с. 258].
В рассматриваемой задаче имеем несколько наблюдений касательно того, какие группы инвесторов могут привлечь свои средства в реализацию ГЧП проекта. В данной задаче необходимо оценить риск данного проекта со стороны привлечения капитала частной стороной. Имеющиеся наблюдения:
y1 = инвесторы группы А;
y2 = инвесторы группы М;
y3 = инвесторы группы A.
Смоделируем условие задачи следующим образом. Модель: yi – независимая величина с одинаковым распределением. Закон распределения будем считать неизвестным, предполагая, что отдельные наблюдения независимы друг от друга, отразим это в виде таблицы, где p и 1 – p – вероятности.
Используемые наблюдения для решения задачи
|
yi |
A |
M |
|
p |
p |
1 – p |
Для реализации байесовского подхода в данной задаче, необходимо задать априорное распределение для неизвестного параметра p. Для определения вероятности, присвоенной событию при отсутствии знания, поддерживающего его наступление, рассмотрим следующее. Неизвестным параметром является параметр p. Учитываем ограничение, присущее вероятности (0; 1], получаем следующую функцию плотности:
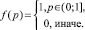(1)
Графическое обозначение полученной функции представлено следующим образом (рис. 1).
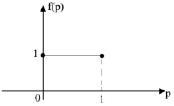
Рис. 1. График априорной функции плотности f(p)
Основной целью решения предлагаемой задачи является вычисление апостериорной функции плотности f(p) при искомых коэффициентах y1, y2, y3 Для дальнейшего хода решения за ключевое условие примем, что «А больше, чем М». Согласно формуле условной вероятности (2), а также условию задачи все факторы, не зависящие от параметра p, будут являться константой:
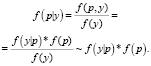(2)
Согласно модели, которой были обозначены данные, отдельные наблюдения являются независимыми. В данном случае при расчете апостериорной функции получаем
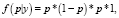(3)
где p*(1 – p)*p – отображение заданной модели, 1 – из априорной функции плотности при p∈[0; 1] (рис. 1).
Соответственно, с точностью до константы, удалось получить вид апостериорной функции. Также, имея данные о том, что распределение вероятности p соответствует промежутку [0; 1], становится возможным произвести вычисление константы. Для этого стоит учесть условие
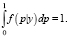(4)
Затем, для точного определения условной функции плотности необходимо вычислить интеграл из смоделированного отображения данных заданной ранее модели, что приведет к получению следующего результата, отражающего апостериорную функцию
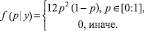(5)
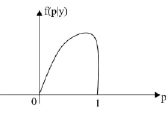
Рис. 2. График апостериорной функции плотности f(p)
График апостериорной функции плотности примет следующий вид (рис. 2).
Сравнивая графики априорной и апостериорной функций плотности можно заметить, что до выяснения некоторого условия (в данном случае – константы) все точки на промежутке (0; 1] кажутся одинаково предпочтительными. Однако график функции апостериорной функции плотности показывает, что вероятность привлечения инвесторов группы А гораздо ближе к 1, чем к 0. Соответственно, становится возможным ответить на вопрос об оценке шансов того, что вероятность привлечения инвесторов группы А больше 0,5:
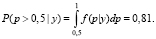(6)
Соответственно, с учетом условий для априорного распределения подразумевалось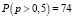 
, а при расчете апостериорного распределения полученный результат равен 
.
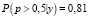Также для того, чтобы отметить существенную разницу между предполагаемым результатом до получения наблюдений (априорным распределением) и полученным в результате вычислений (апостериорным), необходимо провести расчет математического ожидания как при неизвестных, так и при уже полученных наблюдениях:
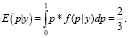(7)
Предполагаемый результат при соблюдении условий для априорного распределения равен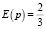 
, соответственно, математическое ожидание с учетом полученных в ходе вычисления наблюдений равно 
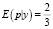, поскольку предполагалось условие «А больше, чем М».
Выводы
Данная искусственно смоделированная задача показала эффективное решение проблемы вычисления вероятности при заранее неизвестных наблюдениях. Путем вычисления априорного и апостериорного распределения, а также их сравнения были получены результаты, которые так или иначе сопоставимы с предполагаемыми. Это объясняется тем, что при расчете учитывались все полученные наблюдения, а также параметры, влияющие на исход рассматриваемого события. Таким образом, включая в вычисление результаты имеющихся или заведомо известных данных, можно получить наиболее точный расчет тех или иных рисков. Это особенно важно для предприятий государственно-частного партнерства, поскольку каждый элемент жизненного цикла проекта содержит определенные риски, за расчет которых несут ответственность две стороны – частная и государственная. Только при учете всех рисков проекта вариант его реализации сможет приносить прибыль, что будет констатировать пользу ГЧП государственному управлению. Резюмируя все вышеописанное, можно сделать вывод о том, что суть байесовской эконометрики состоит в том, чтобы из предполагаемой информации получить более точную за счет вычисления влияющих на исход события параметров. Данный метод в результате решения задачи оказался эффективным в вопросе об оценивании рисков на этапе планирования проекта ГЧП, что было доказано на примере искусственно смоделированной задачи. Эффективность рассматриваемого подхода также объясняется и тем, что использование специализированного программного обеспечения, а также особенного математического инструментария не требуется. Использование байесовского подхода способно значительно облегчить задачу оценивания рисков проектов ГЧП, что в перспективе окажет положительное влияние на рост их реализации и упрощения методики работы как со стороны бизнеса, так и со стороны государства.