В основе проводимых нами исследований лежит понятие территориального кластера как достаточно строго определенного конструкта, введенного с периферии экономического анализа в работе Портера [1]. Примечательно, что важнейший тезис книги Портера не комментируется даже несмотря на то, что он подчеркнут её наименованием. Следуя упомянутой работе, будем понимать под «территориально-производственными кластерами» такие структуры, действие которых на экономических агентов различно, в зависимости от того, включены они или нет в число элементов кластера. В терминологии Портера, происходит «выключение» или «смягчение» механизмов конкуренции для предприятий кластера [1]. Этот процесс сопровождается активизацией механизмов сотрудничества в рамках кластера, что в целом приводит к возникновению существенных конкурентных преимуществ по сравнению с не входящими в кластер предприятиями [2].
Фактически кластер – это экономический институт, в котором произошло смещение экономического равновесия от стихийно-конкурентного. В этой интерпретации кластер не обязательно будет «территориальным», он также может быть «производственным» (с соответствующими производственными цепочками) [2].
Для целей настоящей работы будем опираться на подход Портера со следующими уточнениями.
Во-первых, территориально-производственный кластер – это экономическое образование (искусственное или естественное), пользующееся нормативным, либо сложившимся обособленным режимом, приводящим для предприятий кластера к существенному снижению давления конкуренции, в первую очередь со стороны предприятий, входящих в кластер, а также со стороны всех внешних по отношению к кластеру экономических агентов (что не менее важно!).
Таким образом, и это во-вторых, речь идет об институционально обособленной экономической структуре, обособленность которой (например – правовую) удобно (но не обязательно!) представлять в виде наличия некоторых территориальных границ. Вместе с тем именно территориальный характер границ принципиально факультативен, и когда речь идет о «производственном» кластере, такие границы можно представить (как это делается в физике) в некотором «изотопическом» пространстве, т.е. пространстве, образованном не обязательно физическими пространственными переменными, но переменными, существенно характеризующими производственный цикл. На практике так сложилось, что возникновение тех или иных обособленных режимов носит либо территориальный, либо отраслевой характер. Иные возможные механизмы обособления не рассматриваются, хотя их роль в последние годы лишь возрастает. Примером такого «иного механизма обособления» является предпринятое мэром Сан-Франциско директивное снижение аренды в районе Кремниевой долины в послевоенный кризисный период – и именно этот фактор оказался запускным механизмом, который привел к возникновению научно-производственного кластера в этом районе.
В-третьих, согласно Портеру, следует отличать естественно сложившиеся территориальные кластеры от искусственно созданных. Впрочем, по мнению авторов, такое различие далеко не всегда носит принципиальный характер. Различие по принципу «наличие преференций» и «директивно созданное» может быть несущественным уже по следующему основанию: функционирование директивно созданного кластера становится возможным лишь в силу имеющихся экономических причин, превращающих его в самоподдерживающуюся структуру. Это реализуется лишь при попадании системы в некую институциональную ловушку. Задача внешних игроков, таким образом, сводится к продуцированию (формированию) соответствующей институциональной ловушки [3, 4], которая может лежать в самых разных сферах: от банковского дела [5] до высшего образования [6].
В-четвертых, развитие кластера может происходить как за счет поглощения уже имеющихся ресурсов («экспансионистского развития»), так и за счет вновь создаваемых ресурсов (т.е. «инновационного развития») [1, 2]. Наиболее известным примером такого «кластерного экспансионизма» служит английское огораживание [7]. В наше время такой процесс проявляется в виде слияния или поглощения компаний. Инновационный же кластер создает дополнительные ресурсы, являясь основой для дальнейшего развития других секторов экономики. Экспансионистское развитие кластеров возможно по различным каналам. Первый канал – это присвоение ресурсов собственной экономики. Таковыми ресурсами могут быть как общеэкономические ресурсы, необходимые многим или всем отраслям экономики, так и специфические для данной отрасли. Такой тип «кластера» принято считать «вредным», а такое экономическое поведение характеризовать экономическим термином «монополия».
Второй канал – присвоение ресурсов мировой экономики. В этом случае кластеры выступают в роли национальных агентов межстрановой конкуренции, обеспечивающих смещение экономического равновесия в строго национальных интересах. Данные кластеры также следует отличать от инновационных, т.е. тех, которые способны «продуцировать» ресурсы.
Вместе с тем в экономической действительности, по мнению авторов, нет чистого типа кластеров. Любой из них в той или иной степени функционирует по перечисленным каналам, исключение может составить лишь инновационный канал.
При «выключении» инновационного канала мы получаем экономическую модель без роста. Иными словами, такой подход близок к концепции межотраслевого баланса, исходящего из представления о наличии некоторых «интегралов движения», остающихся неизменными в ходе последовательных стадий экономической деятельности – естественно, в целом по замкнутой экономике [8]. Конечно, в модели межотраслевого баланса, как и в любой топологически сходной модели, вполне возможно «ручное» введение экономического роста, однако оно ему не имманентно, что подтверждается тем, что его можно исключить линейными преобразованиями переменных.
Цель исследования состояла в поиске математического критерия, позволяющего различать инновационные кластеры на основании их динамики по сравнению с неинновационными.
Методы исследования включали в себя традиционные статистические подходы, применяемые в случае перераспределения ограниченных ресурсов. Авторы, опираясь на модель Лифшица – Слезова – Вагнера для стадии коалесценции фазовых переходов первого рода, предлагают подход по определению количественных характеристик неинновационного кластера в асимптотическом случае. Ожидается, что для инновационного развития будут характерны существенные отклонения от найденных асимптотических решений. Анализ получаемых решений и их перенос на конкретные примеры и эконометрические задачи представляет собой следующий этап работ.
Результаты исследования и их обсуждение
В современной экономической теории вопрос «законов сохранения» и ресурсных ограничений во многом выведен за скобки. Теория преимущественно апеллирует двухпараметрическими моделями, агрегируя разнозначные факторы через их стоимость. Ядром такого подхода является модель «спрос-предложение» где в качестве двух параметров выступают объемы продажи или купли и цена условной единицы товара при данном объеме. Таким образом, различные по своей институциональной природе факторы сводятся к их стоимостному выражению.
Вместе с тем изначально экономическая теория строилась иначе. Факторы рассматривались как самостоятельные. Так, в классическом труде Давида Рикардо [9] такими самостоятельными факторами являются физические объемы продуктов, обеспечивающих воспроизводство рабочей силы, отдельно физические объемы зерна, физические объёмы средств производства, физические объёмы сырьевых ресурсов, отдельно объемы вовлеченной пахотной земли различной категории качества, физические объемы производства металлов (рудники) и пр. Также в качестве параметра рассматривается переменное и сбалансированное количество воспроизводящейся рабочей силы и воспроизводящего его населения.
Рикардо проводит различный анализ баланса этих факторов, ведущих себя крайне разнородно: учение об аренде кардинально отличается от учения единой нормы прибыли с капитала. Эти факторы не сводимы друг к другу. Нельзя все сводить к труду, как это приписывают Марксу [7], нельзя все сводить к финансам, как это делает современный экономический мейнстрим. По Рикардо модель экономики с неизбежностью многопараметрическая.
Для многопараметрических моделей имманентна и ещё одна принципиальная черта – наличие масштабов. Данные масштабы суть текущие и слабопеременные экономические факторы, понимаемые как количества и/или как текущий запас. Эти количества соотносятся между собой вне связи с их денежным измерением [9]. Так, например, «Капитал есть та часть богатства страны, которая … [необходима] чтобы привести в движение труд» [9, c. 86]. Но, и это важно, таким масштабом могут выступать различные экономические факторы – как интегральные (капитал, человеческий капитал), так и однородные (зерно, металлы, специалисты).
В современной экономике такими самостоятельными факторами, не сводимыми к стоимостным показателям, обладающими в кратко-, а возможно и в среднесрочной перспективе относительным постоянством и тем самым задающими масштаб, могут быть самые разные экономические факторы. Например, упомянем такой параметр, как «объемы рынка», понимаемый как относительно устойчивая величина спроса на специфический вид товара. Аналогичными по смыслу будут такие переменные, как объем производства сырьевых товаров, например редких металлов, черных и цветных металлов, а также электроэнергии, моторных топлив и прочего. В этом же списке могут быть – и будут – нематериальные активы, создаваемые институционально (такие, как права на интеллектуальную собственность (ключевые патенты), права на диапазоны частот, на воздушные перевозки и многое другое).
Повторим, речь идет о параметрах экономической модели, которые задают масштаб, являются в рассматриваемой временной перспективе ресурсом (запасом) и в этом же временном горизонте достаточно постоянны. Такой ресурс – объект экономического разделения (присвоения) между различными агентами.
Авторы в своей модели исходят из гипотезы, что при инновационном типе развития существуют один или несколько экономических факторов, будь то производственные мощности микро- и наноэлектроники, количества редких металлов, используемых в нелинейной оптике для удвоения частоты, диапазоны частот при развитии 4G-телефонии, количества IT-специалистов в области искусственного интеллекта и прочее и прочее – факторов, обладающих вышеописанными свойствами и участвующих в процессе разделения между динамически растущими и деградирующими кластерами в условиях постоянства общего для них «ресурса».
В рамках этих взглядов для описания инновационных кластеров нами развивается альтернативный динамический подход, заключающийся в описании таких кластеров в виде цепочек (или систем) взаимодействующих нелинейных уравнений по совокупности переменных, описывающих инновационный кластер [10]. Такой подход аналогичен описанию взаимодействия точечных частиц в физике до возникновения статистики.
Вместе с тем означенный подход требует своего развития, прежде всего в определении моделей тех институтов, которые носят принципиальный характер для современной инновационной экономики. Экономические структуры, принципиально необходимые для инновационного развития экономики, как в целом, так и для внедрения отдельной конкретной инновации, разнообразны: от технологических пакетов до территориально-производственных кластеров [11, 12].
В целях разграничения различного типа роста (инновационного/неинновационного), по мнению авторов, достаточно рассмотреть модель неинновационного развития кластера – т.е. модель с действующими «законами сохранения» и ресурсными ограничениями. Получившееся же решение следует рассматривать как «границу», отличающую неинновационную и инновационную области решений. Отметим, что данный подход использует функцию распределения по параметру, характеризующему размер кластера, вводимую по аналогии с аналитической моделью Лифшица – Слезова – Вагнера для стадии коалесценции фазовых переходов первого рода [13]. Несмотря на то, что отказ от рассмотрения динамики роста кластеров в их взаимодействии является, безусловно, шагом назад по отношению к современным экономическим трендам, такой шаг оправдан результатами, которые удается получить.
Для получения этих решений будем считать эволюцию кластеров достаточно независимой, так что можно ввести функцию распределения, зависящую от параметров одного кластера. В качестве параметра, характеризующего кластер, выберем количество принадлежащих ему ресурсов, его объем V, который может иметь смысл численности сотрудников, занимаемых площадей, годового бюджета и т.п. Вообще говоря, функция распределения может зависеть от нескольких параметров, но для простоты мы будем предполагать, что остальные параметры связаны с объемом некоторым «уравнением состояния» и, таким образом, могут быть исключены. Введем далее линейный размер кластера R, связанный с объемом соотношением
V = ARd, (1)
где A – некоторая константа, а d – размерность.
На рассматриваемой стадии, когда процессы образования новых кластеров (естественным или директивным образом) практически завершены, функция распределения кластеров по размерам f(R, t) удовлетворяет уравнению непрерывности, в котором dR/dt рассматривается как скорость перемещения кластера в пространстве линейных размеров:
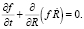(2)
Нормировку функции распределения выберем так, чтобы получить общее число кластеров:
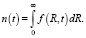(3)
Скорость изменения объема кластера равна результирующему потоку ресурсов к нему:
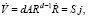(4)
где j – плотность потока ресурсов,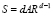 
– размер граничной поверхности кластера.
Таким образом, скорость роста
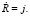(5)
Плотность потока ресурсов может быть найдена из стационарного уравнения диффузии в предположении адиабатической подстройки концентрации ресурсов к размеру кластера:
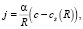(6)
где α – постоянная, определяющая подвижность ресурсов. Здесь мы не будем рассматривать такие случаи, когда поток ресурсов может определяться не только размером граничной поверхности самого кластера, но и другими факторами.
В выражении (6) средняя концентрация ресурсов c является общим для всех кластеров внешним параметром, контролирующим процесс эволюции всей системы, а равновесная концентрация вблизи каждого кластера cs(R) определяется самопроизвольным, «тепловым» высвобождением ресурсов кластером размера R. Размер поверхности S влияет как на интенсивность обмена кластера ресурсами с окружающей средой, так и на энергию поверхности:
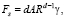(7)
где γ – удельная поверхностная энергия. Изменение энергии поверхности при уменьшении объема на единицу (в качестве которой примем элементарный акт высвобождения ресурса)
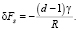(8)
Тогда для равновесной концентрации cs(R) получим
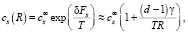(9)
где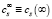 
– равновесная концентрация ресурсов вблизи бесконечно большого кластера, учитывающая изменение свободной энергии системы за счет изменения энтропии и химического потенциала при высвобождении ресурсов. T можно рассматривать как температуру системы, определяющую интенсивность флуктуаций, позволяющих преодолеть энергетический барьер δFs, т.е. мобильность ресурсов. Можно определить величину пересыщения 
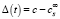, которая уменьшается по мере связывания ресурсов растущими кластерами.
Критический размер кластера соответствует обращению в ноль потока ресурсов (6):
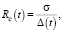
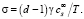(10)
Тогда
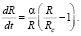(11)
Закон сохранения ресурсов приводит к следующему уравнению баланса:
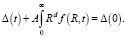(12)
Здесь Δ(0) – полное начальное пересыщение, а интеграл соответствует полному числу ресурсов, связанных кластерами. В случае постоянной генерации ресурсов или их поглощения конкурирующими системами уравнение баланса записывается для больших времен в предположении, что концентрация свободных ресурсов выходит на стационарное значение.
Введем безразмерные величины:
u = R/Rc,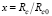 
и 
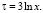(13)
Тогда уравнение (11) запишется в виде
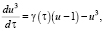(14)
где
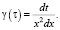(15)
Можно показать [13], что условие (12) при τ → ∞ будет выполняться, если максимум правой части уравнения (14) при u = u0 будет стремиться к нулю (рис. 1). Это возможно при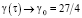 
, при этом u0 = 3/2.
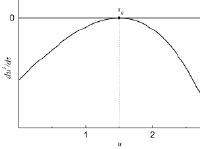
Рис. 1. График функции du3/dτ при γ(τ) = γ0
Тогда скорость роста du/dτ за исключением малой окрестности u0, вклад которой мал, может быть выражена из (14) с γ = γ0:
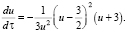(16)
Возвращаясь к исходным переменным, получаем:
Средний размер кластера растет как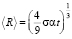 
.
Число кластеров уменьшается со временем по закону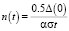 
.
Избыточная концентрация свободных ресурсов стремится к нулю как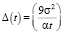 
.
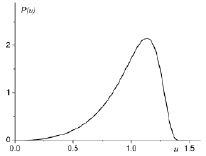
Рис. 2. Автомодельная плотность распределения кластеров по размерам P(u)
Выводы
По сути, данные временные асимптотики как признак неинновационного характера развития кластеров и есть основной результат, который дает этот подход. Подчеркнем, что полученные закономерности характеризуют неинновационное развитие кластеров как системы. Инновационное же развитие характеризуется тем, что для его динамики, как обоснованно ожидается, будут характерны существенные отклонения от предложенных решений. Фиксация таких отклонений будет говорить о наличии других, отличных от рассмотренных, механизмов роста и образования кластеров. Ввиду многовариантности возможных инновационных кластеров эти отклонения также, возможно, многовариантны. Но их наличие является серьезным основанием для предположения об инновационном характере развития кластеров. Предлагаемый подход практически следует рассматривать как «границу», отличающую неинновационную и инновационную области решений.
В отношении концепции «институциональной ловушки» предложенный подход позволяет идентифицировать, является ли процесс формирования инновационных кластеров устойчивым феноменом. Возможно, переход между различной динамикой возникновения кластеров следует интерпретировать как переход между различными институциональными ловушками. При этом разные количественные результаты нельзя интерпретировать как оценочное суждение в отношении выстраиваемых институциональных ловушек. По мнению ряда авторов, затруднительно сказать, является ли институциональная ловушка результатом или причиной стабильности институциональной среды [5, 14].
В рамках рассмотренного нами подхода с очевидностью стоит ряд эконометрических задач. Во-первых, в условиях инновационного развития имеют место значимые структурные сдвиги, что, с очевидностью, не позволяет опираться на стоимостные показатели как исследуемые параметры. Это лишний раз подтверждает настоятельную потребность опираться на «натуральные» показатели, выбираемые в качестве рассматриваемого разделяемого ресурса. Тем самым перед эконометрией ставится задача корректного сбора натуральных показателей, выработки для них нестоимостных критериев агрегации, например, в рамках концепции межотраслевого баланса [8].
Во-вторых, необходим эконометрический же инструмент для выбора в экономическом анализе того или тех параметров, которые могут быть положены в основу предложенного анализа. Это, в частности, означает корректную эконометрическую оценку параметра как стабильного и разделяемого ресурса в рассматриваемом временном горизонте. С очевидностью, данные показатели имеют отраслевую, страновую и другие дифференциации.
И, в-третьих, не только измерение размера кластера (при отказе от ценовых показателей) является серьезной эконометрической задачей, но и, что менее очевидно, их число. Так, в частности, механизмы вертикальной интеграции, неправильно учтенные или проинтерпретированные, могут быть источником возможных неверных оценок [15].
В заключение подчеркнем, что целью настоящей работы была демонстрация того, что хорошо работающие физические модели могут оказаться полезными и для изучения экономики (см. схожие подходы, например, в [16, 17]), хотя возникающих при таком исследовании вопросов может оказаться больше, чем ответов. Тем не менее на этом пути можно получать весьма полезные результаты, а возникающие вопросы могут оказаться сильным стимулом для дальнейших исследований.
Работа выполнена при поддержке гранта РФФИ 20-010-00576.