Применение балансовых моделей охватывает широкий спектр. Их применяют как внутри отдельного хозяйствующего субъекта, региона, страны, так и нескольких стран, объединённых экономическим союзом. Немалое количество работ посвящено исследованию балансовых моделей [1–3].
Известно, что балансовая модель является системой уравнения, устанавливающей баланс между производимой отраслями продукцией и потребностью в ней. К одной из таких моделей относится модель Леонтьева [4–6].
Рассмотрим модель Леонтьева вида:
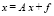(1)
или
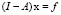, (2)
где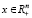 
– вектор, элементы которого обозначают объемы валовых выпусков отраслей 
;
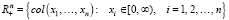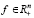– вектор, элементы которого обозначают объемы конечного спроса отраслей;
A – квадратная матрица с элементами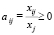 
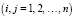, которые обозначают расходы продукта i-й отрасли в j-й отрасли.
Информационному обеспечению данной модели относят матрицу затрат. Так как (1) является статической, то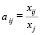 
с течением некоторого периода практически не изменяются.
По некоторым причинам построение матрицы затрат становится проблемным. Обычно при ее построении применяют данные таблицы межотраслевого баланса хозяйствующего субъекта, построенного из статистических данных. Известно, что если построение таблицы межотраслевого баланса по тем или иным причинам становится невозможным, то существует другой метод построения матрицы затрат, который заключается в решении обратной задачи модели (1) при условии, если известны коэффициенты вектора валового выпуска и известны коэффициенты вектора конечного спроса.
К актуальности описанных в работе исследований относятся методы построения матрицы затрат. В работе рассматриваются два метода построения рассматриваемой матрицы. Первым является метод нахождения элементов матрицы затрат из таблицы межотраслевого баланса, построенного из статистических данных хозяйствующего субъекта, а вторым методом нахождения матрицы затрат является решение обратной задачи модели (1). В обоих случаях могут быть погрешности при вычислении. Поэтому для планирования производства в работе применяются матрицы, полученные обоими методами, а также анализируются полученные результаты.
Цель исследования: из статистических данных МСХ КЧР построить таблицу его межотраслевого баланса. Найти элементы матрицы затрат из построенной таблицы межотраслевого баланса МСХ КЧР. Воспользовавшись известным значением вектора конечного спроса и известным значением вектора валового выпуска, найти значение матрицы затрат, решая обратную задачу модели (1). Применить полученные матрицы для нахождения оптимального планирования валового выпуска продукции МСХ КЧР. Проанализировать полученные результаты.
Материалы и методы исследования
В качестве материалов исследования применяются статистические данные за 2015–2019 гг. МСХ КЧР и модель Леонтьева. В работе применяются метод квадратичного программирования – для решения обратной задачи, и метод линейного программирования – для решения оптимизационной задачи.
Результаты исследования и их обсуждение
Рассмотрим два способа построения матрицы затрат балансовой модели.
Известно, что таблица межотраслевого баланса имеет вид (табл. 1).
Рассмотрим взаимосвязь величин табл. 1. Величину xi из табл. 1 связывают с величинами xij и fi следующим соотношением:
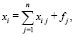
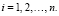
Выразим ее в виде системы уравнений:
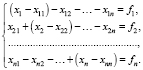(3)
Известно, что коэффициенты aij:
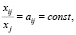
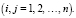
Отсюда найдем:
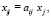
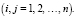
Таблица 1
Общая схема межотраслевого баланса
|
Производящие |
Потребляющие |
Конечный продукт |
Валовой продукт |
||||
|
1 |
2 |
3 |
… |
N |
|||
|
1 2 … n |
x11 x21 … xn1 |
x12 x22 … xn2 |
x13 x23 … xn3 |
… … … … |
x1n x2n … xnn |
f1 f2 … fn |
x1 x2 … xn |
Подставляя последнее выражение в (3), получаем следующую систему уравнений:
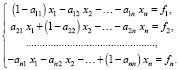(4)
Если выразить
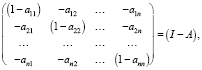
и ввести векторное обозначение:
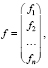
то система (4) запишется в виде (2).
Первый способ построения элементов матрицы затрат – это когда для вычисления элементов матрицы затрат A применяются данные табл. 1, т.е. вычисляются по формуле:
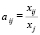. (5)
Во втором способе элементы матрицы затрат A получаем с помощью решения обратной задачи модели (1), по аналогии работы [7] решение сводится:
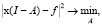(6)
с ограничениями
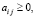
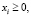
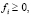
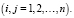(7)
После построения матрицы A применяем методы оптимизации для нахождения оптимального решения модели (2). Пусть в (2)
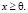(8)
По аналогии работы [8, c. 31] решаем оптимизационную задачу (2), а именно, на множестве решений (2) будем рассматривать целевую функцию:
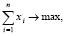(9)
при этом будем предполагать, что xi, i = 1, 2, ..., n, удовлетворяют условиям (2), (8).
Описанную выше методику применим для оптимального планирования производства МСХ КЧР на 2021 г. Для этого применим описанные выше способы построения матрицы затрат.
В начале построим таблицу межотраслевого баланса, для этого используем статистические данные МСХ КЧР за 2015–2019 гг. (тыс. руб.) (табл. 2).
Таблица 2
Таблица межотраслевого баланса МСХ КЧР
|
Производящие |
Потребляющие |
Конечный спрос |
Валовой продукт |
||
|
1 |
2 |
||||
|
1 |
Отрасль растениеводства |
2765,3 |
1382,65 |
9678,6 |
13826,5 |
|
2 |
Отрасль животноводства |
14,83 |
8005,93 |
6805 |
14825,8 |
Из данных табл. 2, вычисляя по формуле (5), получаем:
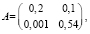
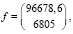
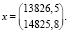
В качестве второго способа построения модели рассмотрим случай, когда известны только две величины балансовой модели, такие как f и x, равные:
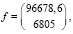
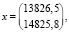
а элементы матрицы A находим с помощью решения задачи квадратичного программирования (6), с ограничениями (7).
Опишем алгоритм решения обратной задачи модели (1) в программе Microsoft Excel.
1. Вводим элементы единичной матрицы I, той же размерности что и A.
2. Вводим начальные значения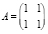 
.
3. Вводим значения элементов вектора x.
4. Вводим значения элементов вектора f.
5. Вычисляем (I – A).
6. Вычисляем (I – A)x.
7. Вычисляем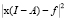 
.
8. Вводим целевую функцию (6) и ограничения (7).
9. Вводим параметры поиска решения.
Применяя описанный алгоритм в программе Microsoft Excel, получаем следующий результат:
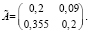
Из полученных результатов видно, что результаты, полученные a11 и a12 в обоих случаях, не имеют существенных отличий. Значение коэффициента a21 во втором случае на 0,354 больше, чем в первом, а значение a22 в первом случае на 0,34 больше, чем во втором.
Далее рассмотрим, как влияют отличия в полученных матрицах на результаты решений оптимизационного планирования производства МСХ КЧР. Для этого найдем оптимальное планирование производства МСХ КЧР с применением полученных матриц.
Найдем оптимальную величину валового выпуска для случая, если к концу 2021 г. МСХ КЧР запланирует увеличить величину конечного спроса на 40 %, т.е.
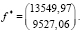
Опишем алгоритм решения задачи (9) с ограничениями (2), (8) в программе Microsoft Excel с применением матрицы затрат, которая была получена из табл. 2.
1. Вводим I той же размерности, что и A.
2. Вводим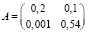 
.
3. Вводим запланированное значение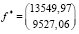 
.
4. Вводим в качестве начальных значений вектора x: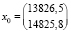 
.
5. Вычисляем (I – A).
6. Вычисляем (I – A)x0.
7. Вводим (9).
8. Вводим ограничение (2) и (8).
9. Вводим параметры поиска решения.
Применяя данный алгоритм, получаем следующее решение:
.
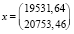По аналогии рассмотрим алгоритм решения задачи в программе Microsoft Excel с применением матрицы затрат, которая была получена с помощью решения обратной задачи модели (2).
1. Вводим I той же размерности, что и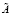 
.
2. Вводим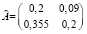 
.
3. Вводим запланированное значение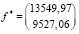 
.
4. Вводим в качестве начальных значений вектора x: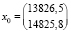 
.
5. Вычисляем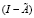 
.
6. Вычисляем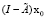 
.
7. Вводим (9).
8. Вводим ограничения (2) и (8).
9. Вводим параметры поиска решения.
Применяя данный алгоритм, получаем следующее решение:
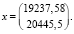
Сравним результаты решения задачи. Решая задачу с помощью матрицы затрат, которая была получена из таблицы межотраслевого баланса МСХ КЧР, получили x1 = 19531,64, x2 = 20753,46. Решая задачу с помощью матрицы затрат, полученной путем решения обратной задачи, получили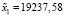 
, 
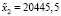. Рассматривая разницу результатов решения в процентах, получим, что результат решения первой отрасли при решении задачи с помощью матрицы затрат, полученной из решения обратной задачи (1), на 1,5 % меньше результата решения с применением матрицы затрат, которая была построена из таблицы межотраслевого баланса МСХ КЧР. Результаты второй отрасли, при решении задачи с помощью матрицы затрат, полученной из решения обратной задачи, на 1,4 % меньше результата решения с применением матрицы затрат, построенной из таблицы межотраслевого баланса МСХ КЧР.
Выводы
Таким образом, из результатов исследования видно, что результаты оптимального планирования производства МСХ КЧР на 2021 г., полученные с применением матрицы затрат, построенной из статистических данных, и результаты оптимального планирования производства МСХ КЧР на 2021 год, полученные с применением матрицы затрат, полученной из решения обратной задачи, отличаются на 1,5 %.
Результаты данной работы можно применить для построения и решения балансовых моделей хозяйствующих субъектов.