Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В стационарных эконометрических моделях значение результирующей переменной зависит от одновременных значений ее факторных признаков, то есть от текущего состояния экономической системы. В динамических системах значения переменной зависят от ее значений в предыдущие моменты времени, то есть ее значений со сдвигом по времени на один шаг назад. Это означает, что поведение системы зависит не только от ее текущего состояния, но и от траектории изменения системы. Эконометрическая модель такого типа представляет собой не функцию объясняющих переменных, а функционал от траектории экономических переменных.

Начало использования динамических эконометрических моделей можно отнести к диссертации Луи Башелье 1900 г., в которой была описана динамика поведения французских государственных облигаций, схожая с броуновским движением.

В 1987 г. Нельсон и Плоссер показали, что коэффициенты регрессии почти всех исторических макроэкономических рядов США являются статистически значимыми, то есть стандартные тесты регрессионного анализа не диагностируют нарушений предпосылок классической модели, но при этом никакой зависимости между экономическими показателями нет. Эти факты заставили пересмотреть все до тех пор полученные эконометрические результаты в области анализа экономических моделей [1; 2].

Целью работы является исследование статистических данных по средней заработной плате на территории Российской Федерации – изучаемый временной ряд не является стационарным. На данном примере покажем необходимые преобразования для использования модели АРПСС и ее применимость для прогнозирования будущих значений рядов.

Материалы и методы исследования

Для описания стационарных случайных процессов используется общая линейная модель, имеющая скорее теоретическое значение, так как ее трудно обрабатывать. На практике применяют частные модели, описываемые небольшим числом параметров.

В 1938 г. Вольд доказал, что стационарный случайный процесс может быть представлен в виде линейной комбинации прошлых возмущений, или белого шума с нулевым математическим ожиданием:

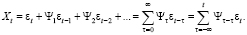(1)

В операторной форме для обратимого процесса (1) имеем:

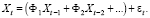(2)

Из (2) следует, что для обратимой общей линейной модели текущее значение процесса является линейной комбинацией всех его прошлых значений и случайного возмущения, не коррелирующего с этими значениями, т.е. можно построить прогнозное значение 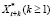по его прошлым значениям [3].

Случайный процесс называется процессом скользящего среднего (moving average) порядка q, сокращенно MA(q), если в его разложении Вольда присутствует q слагаемых. Пусть 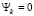при k > q, тогда разложение (1) примет вид:

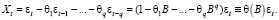
Если известны все значения 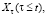то прогнозное значение 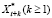с учетом равенств 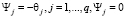при j > q примет вид:

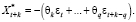
Таким образом, в модели скользящего среднего порядка q можно построить прогноз максимум на q шагов вперед: при этом среднеквадратическая ошибк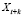а равна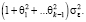

Другой класс моделей с конечным числом параметров можно получить в предположении, что обращенная форма общей линейной модели (1) содержит лишь конечное число членов. Пусть Фk = 0 при k > p, тогда (1) можно записать в следующем виде:

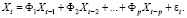(3)

Конечное число членов в разложении (3) определяется порядком p модели авторегрессии, или AR(p).

За счет подбора порядков p и q в описанных моделях можно удовлетворительно описывать многие реальные процессы. На практике для получения большей гибкости в подгонке модели к исследуемым рядам бывает целесообразно объединить авторегрессию и скользящее среднее таким образом, чтобы построить наиболее простую модель, дающую хорошую аппроксимацию при малом количестве параметров. Такая модель носит название ARMA (p, q) и описывается уравнением:

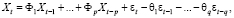(4)

Пусть требуется построить прогноз 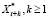, k ≤ q по имеющимся наблюдениям 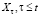. Тогда по (4)

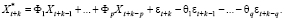
Далее рассмотрим модель

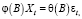(5)

где φ(B) – нестационарный оператор авторегрессии порядка p + d, такой, что d корней уравнения φ(B) = 0 равны единице, а остальные p корней лежат вне единичного круга; θ(B) – оператор скользящего среднего. Тогда (5) можно записать в следующем виде:

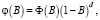(6)

где Ф(B) – стационарный оператор авторегрессии порядка p. Если ввести разностный оператор 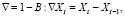то φ(B) запишется как 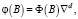и (6) можно записать в виде

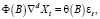(7)

где 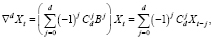и, следовательно, (7) уже является стационарным обратимым процессом ARMA(p,q). Если ввести обратный к ∇ оператор 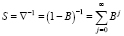, называемый оператором суммирования, то из (10) следует, что

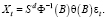
Таким образом, процесс {Xt} можно получить d-кратным интегрированием стационарного процесса (7), т.е. процесс {Xt} получается из белого шума εt с помощью трех операций фильтрации: скользящего среднего θ(B), стационарной авторегрессии Ф–1(B) и суммирования Sd [3].

Для прогнозирования временных рядов с помощью моделей авторегрессии и проинтегрированного скользящего среднего воспользуемся прикладным программным пакетом Statistica 12. Для работы потребуется модуль Times Series/Forecasting, раздел ARIMA & autocorrelation functions [4].

Рассмотрим данные о среднемесячной заработной плате по РФ за период 2013–2019 гг. [5] Для анализа используем данные за 2013–2018 гг. (табл. 1), чтобы сравнить прогноз с фактическими данными за 2019 год для корректировки значений.

Таблица 1

Средние месячные заработные платы по РФ в 2013–2019 гг.

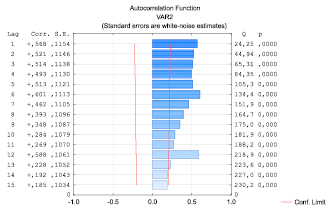
Рис. 1. Функция автокорреляции остатков

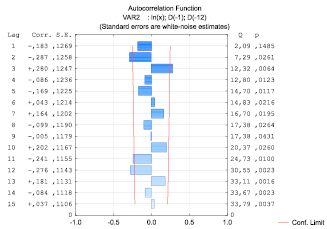
Рис. 2. Функция автокорреляции остатков

Формально мы можем прогнозировать только стационарные ряды. Для того чтобы работать с представленным выше рядом, необходимо провести преобразования, суть которых заключается в том, чтобы избавиться от коррелированности остатков (стандартных ошибок). Для исходного ряда функция автокорреляции выглядит следующим образом (рис. 1).

Отметим, что остатки коррелированы, и необходимо применить разностный оператор. Кроме того, сильно коррелированы остатки с лагом 12, поэтому в модели нужно использовать сезонную компоненту с данным лагом.

Преобразуем исходный ряд: прологарифмируем и применим разностный оператор второго порядка с лагами 1 и 12. Для нового ряда функция автокорреляции примет вид (рис. 2).

Количество статистически значимых коэффициентов определяет порядок модели ARMA(p, q). Можно отметить, что по функции убывания коэффициентов автокорреляции со временем (лагом) можно судить о том, какие знаки будут принимать коэффициенты модели [6].

С учетом автокорреляции остатков для анализа ряда необходимо применять авторегрессию 2-го порядка с сезонными компонентами Ps = 1, Qs = 1. Результат выполнения алгоритма и оценки параметров представлен ниже (рис. 3).

Программный пакет Statistica автоматически проверяет статистические гипотезы для коэффициентов, поэтому выделенные красным цветом коэффициенты модели являются статистически значимыми (при α = 0,05). В пакете есть возможность построить прогноз на N шагов вперед с доверительным интервалом, а также визуализировать данные (рис. 4).

Табличные значения прогноза и фактические показатели (табл. 2).

Таблица 2

Прогноз модели и фактические данные

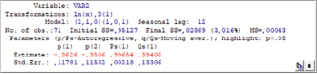
Рис. 3. Оценка модели ARMA(2,0)

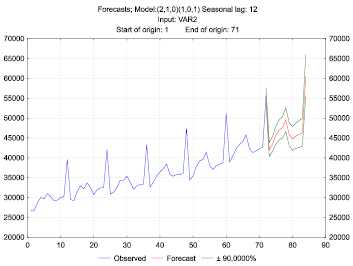
Рис. 4. График прогнозных значений ряда на 12 шагов вперед

Модель ARIMA позволяет строить точечный прогноз для будущих значений временного ряда. В силу того что исследуемый процесс является стохастическим, прогнозное значение также является случайной величиной. Для непрерывных случайных величин необходимо строить интервал, размер которого определяется вероятностью попадания в него реализации случайной величины. С помощью программного пакета Statistica строим доверительный интервал при заданном уровне значимости.

Далее используем данные 2019 г., чтобы сделать модель более точной, и построим прогноз на первое полугодие 2020 г. Сохраним те же настройки модели ARIMA. Полученный результат представлен в табл. 3.

Таблица 3

Прогноз модели на первое полугодие 2020 г.

Результаты исследования и их обсуждение

По имеющимся данным за 2019 г. можно сравнить прогноз ARIMA и фактические значения. Как видно из рис. 1 и табл. 2, модель достаточно точно описывает исследуемый нестационарный процесс, отражая тенденцию ряда и циклические колебания (периоды меньших и больших выплат заработной платы, объясняемые летними сезонами отпусков и декабрьскими премиями). Все фактические значения находятся в пределах построенного доверительного интервала.

Полученные результаты и оценки параметров модели, прошедшие проверку на статистическую значимость, позволяют считать модель адекватной и использовать для прогнозирования исследуемого процесса – изменения среднемесячных заработных плат резидентов РФ. Прогнозные значения на первое полугодие 2020 г. приведены в табл. 3.

Дополнительно можно подбирать разные наборы параметров модели ARIMA, дающие сходные удовлетворительные аппроксимации исследуемого процесса, и использовать усредненный прогноз [7]. При этом не всегда удается найти параметры модели, при которых оценки коэффициентов были бы статистически значимыми. В частных случаях построенная модель может не иметь статистически значимых оценок, но давать адекватный прогноз на прошедшие периоды, что, однако, не позволяет считать модель надежной и использовать для прогнозирования будущих периодов.

Также существуют обобщения и их модификации и аналоги модели ARIMA(p, d, q): ARFIMA(p, d, q), ARFIMA-GARCH(p, d, q) – учитывающие фрактальную размерность исследуемого ряда. Каждый из них имеет свою специфику применения и преимущества [8].

Заключение

При исследовании процессов, описываемых временным рядом, имеющим скрытые закономерности, определяющие изменения числовых показателей процесса, необходимо учитывать их фрактальные свойства. В частных случаях для анализа применяется модель Бокса-Дженкинса, направленная на исследование нестационарных временных рядов. При преобразованиях временного ряда и подборе параметров модели можно получить удовлетворительный прогноз для изучаемого процесса на k шагов с некоторым доверительным интервалом.

Использование модели авторегрессии – проинтегрированного скользящего среднего особенно полезно при исследовании экономических процессов, которые имеют определенную тенденцию и цикличность, поскольку построение точного прогноза будущих экономических показателей необходимо при выборе экономической стратегии государства, предприятия, составления планов производства, хеджирования рисков и управления экономической активностью компаний.