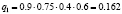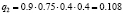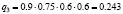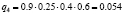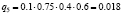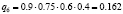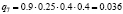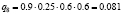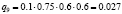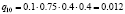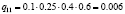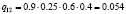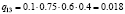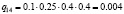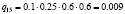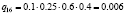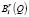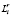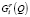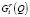Оценка инвестиционных альтернатив и выбор оптимального инвестиционного решения проводится с учетом вариативности развития событий, многокритериальности оптимума и субъективных предпочтений лица, принимающего решение (ЛПР). Реализовать подобный подход к анализу инвестиционных решений позволяет модель игры с природой. Под природой понимается объективная действительность, внешняя среда, окружающая задачу принятия решений.
Формально игра с природой определяется следующим образом.
Множество SΠ = {Π1, Π2,…, Πn} состояний природы формируется на основе анализа возможных сценариев развития событий. В любой момент времени природа может находиться только в одном из n состояний Π1, Π2,…, Πn. Состояния природы, или сценарии, образуют полную группу событий, поэтому соответствующие им вероятности Q = (q1, q2,…, qn) в сумме дают единицу:
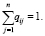 (1)
(1)
Результаты реализации решений игрока (ЛПР) при различных состояниях природы задают платежную матрицу игры V:
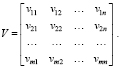 (2)
(2)
Матрица V может иметь смысл матрицы выигрышей или матрицы проигрышей в зависимости от условий задачи. Элемент матрицы vij – это результат реализации i-й стратегии (i-го решения) Ai игрока при j-м состоянии Пj природы.
Исходная матрица игры может быть преобразована в матрицу рисков:
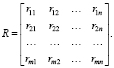 (3)
(3)
Для построения матрицы рисков используются показатели благоприятности состояний природы. Показателем благоприятности состояния Пj природы называется соответствующий этому состоянию максимальный выигрыш ЛПР (наибольший элемент в j-м столбце матрицы V игры):
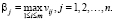 (4)
(4)
Если платежная матрица игры представляет собой матрицу проигрышей, показатель благоприятности j-го состояния природы рассчитывается по формуле:
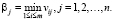 (5)
(5)
Риском rij игрока при выборе им стратегии Ai в условиях состояния природы Пj называется расхождение между показателем благоприятности βj состояния природы Пj и фактическим выигрышем vij. Другими словами, это разность между выигрышем, который игрок получил бы, выбрав лучшую стратегию, если бы знал заранее, что природа примет состояние Пj, и выигрышем, который он получит, выбрав стратегию Ai при этом же состоянии Пj.
Величина риска по матрице выигрышей рассчитывается по формуле:
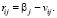 (6)
(6)
Величина риска по матрице проигрышей:
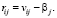 (7)
(7)
Ситуация, когда известны вероятности состояний природы, называется ситуацией принятия решений в условиях риска.
Подробному изложению критериев оптимальности принятия решений и их теоретическому обоснованию посвящена монография Л.Г. Лабскера [1], внесшего значительный вклад в развитие теории игр и развитие теории принятия оптимальных решений. В данной статье рассматриваются некоторые примеры критериев оптимальности, учитывающих информацию о различных исходах развития событий. При этом исходы анализируются и с точки зрения возможных выигрышей, и с точки зрения рисков.
Для решения задачи оптимального распределения инвестиций используются критерии Байеса, Лапласа, Ходжа – Лемана, Гермейера и их модификации. Следует отметить, что данный перечень не исчерпывает возможные подходы к оценке эффективности решений в рамках игры с природой. Могут быть применены и другие критерии оптимальности, общая схема конструирования которых представлена в работе [1, с. 642–658]. Игры с природой и соответствующие им критерии оптимальности применяются для решения самых разнообразных финансово-экономических задач принятия решений: оптимальный выбор корпоративного заемщика [2], оптимальный выбор в индустрии моды [3], оптимизация деятельности фармацевтической фирмы [4], выбор эмитента для финансовых инвестиций [5] и многие другие прикладные задачи.
Целью настоящего исследования является анализ задачи распределения инвестиций с применением комбинированных критериев оптимальности относительно выигрышей и рисков. Применяемые методы исследования – формализация и математизация проблемы многокритериального выбора с учетом субъективных предпочтений ЛПР, в условиях вариативности развития событий. Материал статьи может быть использован в качестве основы для разработки методики многокритериального и многофакторного анализа инвестиционных альтернатив. Для удобства изложения в статье рассматривается задача с числовыми исходными данными.
Постановка задачи
Потенциальный инвестор располагает денежной суммой M = 120, которую намерен полностью вложить в одну компанию (публичное акционерное общество), распределив оптимальным образом инвестиции между инвестиционным проектом, в котором заинтересован, и акциями компании. В качестве возможных долей αi, i = 1,2,…,6, участия в проекте инвестор рассматривает следующие варианты, представленные в табл. 1.
Таблица 1
Варианты долевого участия в инвестиционном проекте
|
Доля αi |
α1 |
α2 |
α3 |
α4 |
α5 |
α6 |
|
1 |
0.75 |
0.5 |
0.3 |
0.1 |
0 |
Остаток денежных средств инвестор вкладывает в акции этой же компании.
Таблица 2
Оценки вероятностей благоприятного и неблагоприятного проявления факторов
|
Фактор, Fi |
Вероятность благоприятного проявления фактора, pi1 |
Вероятность неблагоприятного проявления фактора, pi0 |
|
F1 (уровень спроса на продукцию) |
p11 = 0.9 (достаточный для успешной реализации проекта уровень спроса) |
p10 = 0.1 (недостаточный для успешной реализации проекта уровень спроса) |
|
F2 (знания и опыт менеджеров) |
p21 = 0.75 (знания и опыт менеджеров соответствуют сложности бизнес-ситуации) |
p20 = 0.25 (знания и опыт менеджеров не соответствуют сложности бизнес-ситуации) |
|
F3 (инфляционные ожидания) |
p31 = 0.40 (приемлемый для успешной реализации бизнес-идеи уровень инфляции) |
p30 = 0.60 (неприемлемый для успешной реализации бизнес-идеи уровень инфляции) |
|
F4 (трансакционные издержки) |
p41 = 0.60 (приемлемый для успешной реализации бизнес-идеи уровень трансакционных издержек) |
p40 = 0.40 (неприемлемый для успешной реализации бизнес-идеи уровень трансакционных издержек) |
В качестве факторов, определяющих выбор доли участия в проекте, инвестор рассматривает уровень спроса на продукцию (F1), знания и опыт управляющей команды (F2), инфляционные ожидания (F3) и трансакционные издержки (F4). Известно, что вероятность достаточного для успешной реализации проекта спроса на продукцию составляет 90 %. Доверие к знаниям и опыту управляющей команды инвесторы оценивают на уровне 75 %. Инфляционные ожидания и трансакционные издержки позволят успешно реализовать проект с вероятностью соответственно 40 % и 60 %. Далее будем предполагать, что, если i-й фактор проявит себя благоприятно, соответствующая переменная Fi = 1, иначе Fi = 0, i = 1, 2, 3, 4. Вероятность благоприятного проявления i-го фактора обозначим символом pi1, вероятность неблагоприятного проявления i-го фактора обозначим символом pi0, i = 1, 2, 3, 4. Для вероятностей pi1 и pi0 выполняется условие pi1 + pi0 = 1, i = 1, 2, 3, 4, так как случайная величина Fi принимает только два значения: единица и ноль, исходя из вышеизложенного предположения. Оценки вероятностей благоприятного и неблагоприятного проявления факторов приведены в табл. 2.
Различные комбинации благоприятного и неблагоприятного проявления факторов образуют n = 24 = 16 сценариев Sj, j = 1, 2,…, 16 (табл. 3). Факторы Fi, i = 1, 2, 3, 4, проявляют себя независимо, поэтому вероятности qj, j = 1, 2,…, 24, реализации сценариев определим в соответствии с правилом умножения вероятностей независимых событий (табл. 3).
Таблица 3
Вероятности реализации сценариев развития событий
|
j |
F1 |
F2 |
F2 |
F4 |
qj |
|
1 |
1 |
1 |
1 |
1 |
|
|
2 |
1 |
1 |
1 |
0 |
|
|
3 |
1 |
1 |
0 |
1 |
|
|
4 |
1 |
0 |
1 |
1 |
|
|
5 |
0 |
1 |
1 |
1 |
|
|
6 |
1 |
1 |
0 |
0 |
|
|
7 |
1 |
0 |
1 |
0 |
|
|
8 |
1 |
0 |
0 |
1 |
|
|
9 |
0 |
1 |
0 |
1 |
|
|
10 |
0 |
1 |
1 |
0 |
|
|
11 |
0 |
0 |
1 |
1 |
|
|
12 |
1 |
0 |
0 |
0 |
|
|
13 |
0 |
1 |
0 |
0 |
|
|
14 |
0 |
0 |
1 |
0 |
|
|
15 |
0 |
0 |
0 |
1 |
|
|
16 |
0 |
0 |
0 |
0 |
|
В табл. 3 сценарии упорядочены по убыванию предпочтительности для инвестора. Предпочтительность сценария обусловлена ожидаемой отдачей от инвестиций. Будем предполагать, что оценки стоимости денежных потоков V, при 100 % финансировании проекта, инвестору известны для каждого варианта развития событий. Отдачу от финансовых инвестиций R инвестор связывает с качеством управляющей команды. Инвестор предполагает, что, если знания и опыт менеджеров окажутся достаточными для успешной реализации проекта, стоимость акций компании поднимается на 16 %, если недостаточными – стоимость акций понизится на 5 %. Прогнозные оценки V приведены в табл. 4.
Таблица 4
Ожидаемая отдача от инвестиций при различных сценариях развития событий
|
j |
F1 |
F2 |
F2 |
F4 |
Vj, ден. ед. |
Rj |
|
1 |
1 |
1 |
1 |
1 |
180 |
+0.16 |
|
2 |
1 |
1 |
1 |
0 |
170 |
+0.16 |
|
3 |
1 |
1 |
0 |
1 |
165 |
+0.16 |
|
4 |
1 |
0 |
1 |
1 |
160 |
–0.05 |
|
5 |
0 |
1 |
1 |
1 |
155 |
+0.16 |
|
6 |
1 |
1 |
0 |
0 |
145 |
+0.16 |
|
7 |
1 |
0 |
1 |
0 |
140 |
–0.05 |
|
8 |
1 |
0 |
0 |
1 |
135 |
–0.05 |
|
9 |
0 |
1 |
0 |
1 |
130 |
+0.16 |
|
10 |
0 |
1 |
1 |
0 |
125 |
+0.16 |
|
11 |
0 |
0 |
1 |
1 |
120 |
–0.05 |
|
12 |
1 |
0 |
0 |
0 |
110 |
–0.05 |
|
13 |
0 |
1 |
0 |
0 |
105 |
+0.16 |
|
14 |
0 |
0 |
1 |
0 |
100 |
–0.05 |
|
15 |
0 |
0 |
0 |
1 |
95 |
–0.05 |
|
16 |
0 |
0 |
0 |
0 |
85 |
–0.05 |
Обозначим символом vij прибыль инвестора в ситуации выбора доли участия в проекте αi в условиях сценария развития событий Si. Соответствующая исходным данным формула расчета прибыли инвестора будет иметь вид
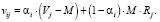 (8)
(8)
Соответствующая задаче матрица выигрышей (прибыли) инвестора примет вид (табл. 5).
Критерий Байеса относительно выигрышей и метод идеальной точки
Многокритериальный выбор варианта долевого участия определяется вектором показателей качества альтернативных инвестиционных решений αi:
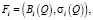 (9)
(9)
где 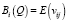 – математическое ожидание случайной величины выигрыша инвестора в случае выбора им доли финансирования инвестиционного проекта αi;
– математическое ожидание случайной величины выигрыша инвестора в случае выбора им доли финансирования инвестиционного проекта αi;
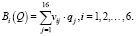 (10)
(10)
σi(Q) – среднее квадратическое отклонение случайной величины выигрыша, которое характеризует разброс возможных значений выигрыша vij вокруг среднего ожидаемого значения E(vij), т.е. может использоваться в качестве меры риска при выборе варианта долевого участия αi;
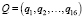 – вектор вероятностей сценариев развития событий.
– вектор вероятностей сценариев развития событий.
Таблица 5
Выигрыши инвестора при различных сценариях развития событий
|
Матрица выигрышей инвестора |
Сценарии развития событий |
|||||||||||||||||
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
S8 |
S9 |
S10 |
S11 |
S12 |
S13 |
S14 |
S15 |
S16 |
|||
|
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
R8 |
R9 |
R10 |
R11 |
R12 |
R13 |
R14 |
R15 |
R16 |
|||
|
0.16 |
0.16 |
0.16 |
-0.05 |
0.16 |
0.16 |
-0.05 |
-0.05 |
0.16 |
0.16 |
-0.05 |
-0.05 |
0.16 |
-0.05 |
-0.05 |
-0.05 |
|||
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
V16 |
|||
|
180 |
170 |
165 |
160 |
155 |
145 |
140 |
135 |
130 |
125 |
120 |
110 |
105 |
100 |
95 |
85 |
|||
|
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
q7 |
q8 |
q9 |
q10 |
q11 |
q12 |
q13 |
q14 |
q15 |
q16 |
|||
|
0.162 |
0.108 |
0.243 |
0.054 |
0.018 |
0.162 |
0.036 |
0.081 |
0.027 |
0.012 |
0.006 |
0.054 |
0.018 |
0.004 |
0.009 |
0.006 |
|||
|
Долевое участие |
α1 |
1.00 |
60 |
50 |
45 |
40 |
35 |
25 |
20 |
15 |
10 |
5 |
0 |
-10 |
-15 |
-20 |
-25 |
-35 |
|
α2 |
0.75 |
49.8 |
42.3 |
38.55 |
28.5 |
31.05 |
23.55 |
13.5 |
9.75 |
12.3 |
8.55 |
-1.5 |
-9 |
-6.45 |
-10.2 |
-20.25 |
-27.75 |
|
|
α3 |
0.50 |
39.6 |
34.6 |
32.1 |
17 |
27.1 |
22.1 |
7 |
4.5 |
14.6 |
12.1 |
-3 |
-8 |
2.1 |
-0.4 |
-15.5 |
-20.5 |
|
|
α4 |
0.30 |
31.44 |
28.44 |
26.94 |
7.8 |
23.94 |
20.94 |
1.8 |
0.3 |
16.44 |
14.94 |
-4.2 |
-7.2 |
8.94 |
7.44 |
-11.7 |
-14.7 |
|
|
α5 |
0.10 |
23.28 |
22.28 |
21.78 |
-1.4 |
20.78 |
19.78 |
-3.4 |
-3.9 |
18.28 |
17.78 |
-5.4 |
-6.4 |
15.78 |
15.28 |
-7.9 |
-8.9 |
|
|
α6 |
0.00 |
19.2 |
19.2 |
19.2 |
-6 |
19.2 |
19.2 |
-6 |
-6 |
19.2 |
19.2 |
-6 |
-6 |
19.2 |
19.2 |
-6 |
-6 |
|
Соответствующий вектору Fi показателей качества выбора αi векторный критерий оптимальности имеет вид
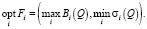 (11)
(11)
Для поиска оптимального решения воспользуемся методом идеальной точки. Идеальная точка представляет собой пару
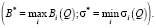 (12)
(12)
Метод идеальной точки предполагает построение функции свертки
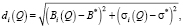 (13)
(13)
значениями которой являются расстояния в пространстве векторных оценок от фактической альтернативы (конкретного варианта долевого участия) αi до идеальной (утопической) альтернативы α*, оценкой которой является пара (E*, σ*). Лучшим вариантом долевого участия 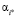 будет альтернатива, которая наиболее близка по своим характеристикам к идеальному варианту:
будет альтернатива, которая наиболее близка по своим характеристикам к идеальному варианту:
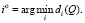 (14)
(14)
Запишем результаты оценки эффективности вариантов долевого участия (табл. 6).
Таблица 6
Выбор лучшей альтернативы по методу идеальной точки
|
Bi(Q) |
σi(Q) |
di(Q) |
|||
|
Долевое участие |
α1 |
1.00 |
33.84 |
21.68 |
10.82 |
|
α2 |
0.75 |
28.63 |
17.91 |
8.77 |
|
|
α3 |
0.50 |
23.42 |
14.58 |
11.06 |
|
|
α4 |
0.30 |
19.25 |
12.45 |
14.67 |
|
|
α5 |
0.10 |
15.08 |
11.12 |
18.75 |
|
|
α6 |
0.00 |
13.00 |
10.85 |
20.83 |
|
|
Идеальная точка |
33.84 |
10.85 |
|||
На минимальном расстоянии от идеальной точки находится альтернатива
α2 = 0,75,
в соответствии с которой 75 % капитала следует вложить в инвестиционный проект, 25 % – в финансовые активы компании.
Синтетический критерий Байеса
Показатель эффективности по синтетическому критерию Байеса относительно выигрышей и рисков имеет вид
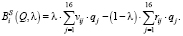 (15)
(15)
Лучшим вариантом долевого участия 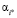 будет альтернатива:
будет альтернатива:
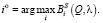 (16)
(16)
Расчет рисков rij в соответствии с формулой (6) представлен в табл. 9.
Параметр λ∈[0; 1] имеет смысл показателя предпочтения выигрышей, который характеризует степень предпочтения ЛПР (значимость для ЛПР) выигрышей перед рисками при выборе решения.
Точное значение параметра λ ЛПР (инвестору) неизвестно, несмотря не субъективность его оценивания. Однако можно предположить, что ЛПР способен выбрать один их интервалов возможных значений λ, наиболее соответствующий его предпочтениям.
Таблица 7
Выбор лучшей альтернативы по синтетическому критерию Байеса
|
Bi(Q) |
|
|||
|
Долевое участие |
α1 |
1.00 |
33.84 |
1.75 |
|
α2 |
0.75 |
28.63 |
6.96 |
|
|
α3 |
0.50 |
23.42 |
12.17 |
|
|
α4 |
0.30 |
19.25 |
16.34 |
|
|
α5 |
0.10 |
15.08 |
20.50 |
|
|
α6 |
0.00 |
13.00 |
22.59 |
|
Наилучшие оценки эффективности решений по критериям Байеса и относительно выигрышей Bi(Q), и относительно рисков 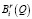 указывают на приоритетность альтернативы α1 = 1 (табл. 7). Это значит, что при любых весовых коэффициентах λ и (1 – λ) лучшей альтернативной по синтетическому критерию Байеса будет α1 = 1.
указывают на приоритетность альтернативы α1 = 1 (табл. 7). Это значит, что при любых весовых коэффициентах λ и (1 – λ) лучшей альтернативной по синтетическому критерию Байеса будет α1 = 1.
Графическое представление альтернативных вариантов участия в инвестиционном проекте приведено на рис. 1. Данные для построения графиков содержатся в табл. 8.
На графике (рис. 1) хорошо видно, что альтернатива α1 = 1 является доминантой, т.е. доминирует над всеми другими альтернативами. Это значит, что по синтетическому критерию Байеса оптимальным решением является 100 % финансирование инвестиционного проекта и отказ от приобретения финансовых активов для любого уровня значимости λ выигрышей и, соответственно, значимости (1 – λ) рисков при сравнительном анализе вариантов финансирования проекта.
Таблица 8
Эффективность вариантов долевого участия в инвестиционном проекте по синтетическому критерию Байеса
|
Степень предпочтения выигрышей при оценке эффективности решений |
|||||||||||||
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|||
|
Долевое участие |
α1 |
1.00 |
-1.75 |
1.81 |
5.37 |
8.92 |
12.48 |
16.04 |
19.60 |
23.16 |
26.72 |
30.28 |
33.84 |
|
α2 |
0.75 |
-6.96 |
-3.40 |
0.16 |
3.72 |
7.27 |
10.83 |
14.39 |
17.95 |
21.51 |
25.07 |
28.63 |
|
|
α3 |
0.50 |
-12.17 |
-8.61 |
-5.05 |
-1.49 |
2.07 |
5.62 |
9.18 |
12.74 |
16.30 |
19.86 |
23.42 |
|
|
α4 |
0.30 |
-16.34 |
-12.78 |
-9.22 |
-5.66 |
-2.10 |
1.46 |
5.02 |
8.57 |
12.13 |
15.69 |
19.25 |
|
|
α5 |
0.10 |
-20.50 |
-16.94 |
-13.39 |
-9.83 |
-6.27 |
-2.71 |
0.85 |
4.41 |
7.97 |
11.53 |
15.08 |
|
|
α6 |
0.00 |
-22.59 |
-19.03 |
-15.47 |
-11.91 |
-8.35 |
-4.79 |
-1.23 |
2.32 |
5.88 |
9.44 |
13.00 |
|
Таблица 9
Возможные потери (риски) инвестора
|
Матрица рисков инвестора |
Сценарии развития событий |
|||||||||||||||||
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
S8 |
S9 |
S10 |
S11 |
S12 |
S13 |
S14 |
S15 |
S16 |
|||
|
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
R8 |
R9 |
R10 |
R11 |
R12 |
R13 |
R14 |
R15 |
R16 |
|||
|
0.16 |
0.16 |
0.16 |
-0.05 |
0.16 |
0.16 |
-0.05 |
-0.05 |
0.16 |
0.16 |
-0.05 |
-0.05 |
0.16 |
-0.05 |
-0.05 |
-0.05 |
|||
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
V16 |
|||
|
180 |
170 |
165 |
160 |
155 |
145 |
140 |
135 |
130 |
125 |
120 |
110 |
105 |
100 |
95 |
85 |
|||
|
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
q7 |
q8 |
q9 |
q10 |
q11 |
q12 |
q13 |
q14 |
q15 |
q16 |
|||
|
0.162 |
0.108 |
0.243 |
0.054 |
0.018 |
0.162 |
0.036 |
0.081 |
0.027 |
0.012 |
0.006 |
0.054 |
0.018 |
0.004 |
0.009 |
0.006 |
|||
|
Долевое участие |
α1 |
1.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
9.20 |
14.20 |
0.00 |
4.00 |
34.20 |
39.20 |
19.00 |
29.00 |
|
α2 |
0.75 |
10.20 |
7.70 |
6.45 |
11.50 |
3.95 |
1.45 |
6.50 |
5.25 |
6.90 |
10.65 |
1.50 |
3.00 |
25.65 |
29.40 |
14.25 |
21.75 |
|
|
α3 |
0.50 |
20.40 |
15.40 |
12.90 |
23.00 |
7.90 |
2.90 |
13.00 |
10.50 |
4.60 |
7.10 |
3.00 |
2.00 |
17.10 |
19.60 |
9.50 |
14.50 |
|
|
α4 |
0.30 |
28.56 |
21.56 |
18.06 |
32.20 |
11.06 |
4.06 |
18.20 |
14.70 |
2.76 |
4.26 |
4.20 |
1.20 |
10.26 |
11.76 |
5.70 |
8.70 |
|
|
α5 |
0.10 |
36.72 |
27.72 |
23.22 |
41.40 |
14.22 |
5.22 |
23.40 |
18.90 |
0.92 |
1.42 |
5.40 |
0.40 |
3.42 |
3.92 |
1.90 |
2.90 |
|
|
α6 |
0.00 |
40.80 |
30.80 |
25.80 |
46.00 |
15.80 |
5.80 |
26.00 |
21.00 |
0.00 |
0.00 |
6.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
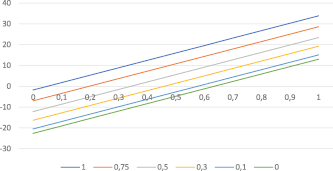
Рис. 1. Альтернативные варианты долевого участия по синтетическому критерию Байеса
Критерий Лапласа и метод идеальной точки
Предположим теперь, что у ЛПР (инвестора) появились серьезные сомнения в достоверности предложенных ему оценок вероятностей благоприятной реализации факторов (табл. 2). При отсутствии достоверной информации о наступлении благоприятных или неблагоприятных событий у ЛПР нет оснований полагать, что одни события более вероятны, чем другие. Поэтому благоприятные и неблагоприятные события инвестор может рассматривать как равновероятные (табл. 10).
Таблица 10
Оценки вероятностей благоприятного и неблагоприятного проявления факторов в рамках критерия Лапласа принятия решений
|
Фактор, Fi |
Вероятность благоприятного проявления фактора, pi1 |
Вероятность неблагоприятного проявления фактора, pi0 |
|
F1 (уровень спроса на продукцию) |
p11 = 0.5 (достаточный для успешной реализации проекта уровень спроса) |
p10 = 0.5 (недостаточный для успешной реализации проекта уровень спроса) |
|
F2 (знания и опыт менеджеров) |
p21 = 0.5 (знания и опыт менеджеров соответствуют сложности бизнес-ситуации) |
p20 = 0.5 (знания и опыт менеджеров не соответствуют сложности бизнес-ситуации) |
|
F3 (инфляционные ожидания) |
p31 = 0.5 (приемлемый для успешной реализации бизнес-идеи уровень инфляции) |
p30 = 0.5 (неприемлемый для успешной реализации бизнес-идеи уровень инфляции) |
|
F4 (трансакционные издержки) |
p41 = 0.50 (приемлемый для успешной реализации бизнес-идеи уровень трансакционных издержек) |
p40 = 0.50 (неприемлемый для успешной реализации бизнес-идеи уровень трансакционных издержек) |
В этом случае равновероятными окажутся и сценарии развития событий:
Q =
|
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
0.0625 |
Показатель эффективности по критерию Лапласа относительно выигрышей имеет вид
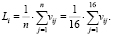 (17)
(17)
Лучшая альтернатива 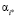 по критерию Лапласа:
по критерию Лапласа:
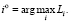 (18)
(18)
Результаты оценки эффективности вариантов долевого участия представлены в табл. 11.
Таблица 11
Выбор лучшей альтернативы по методу идеальной точки
|
Li |
σi |
di |
|||
|
Долевое участие |
α1 |
1.00 |
12.50 |
27.84 |
15.34 |
|
α2 |
0.75 |
11.42 |
22.24 |
9.79 |
|
|
α3 |
0.50 |
10.34 |
17.26 |
5.22 |
|
|
α4 |
0.30 |
9.47 |
14.17 |
3.46 |
|
|
α5 |
0.10 |
8.61 |
12.56 |
3.89 |
|
|
α6 |
0.00 |
8.18 |
12.50 |
4.33 |
|
|
Идеальная точка |
12.50 |
12.50 |
|||
На минимальном расстоянии от идеальной точки находится альтернатива
α4 = 0,30,
в соответствии с которой 30 % капитала следует вложить в инвестиционный проект, 70 % – в финансовые активы компании.
Синтетический критерий Лапласа
Показатель эффективности по синтетическому критерию Лапласа относительно выигрышей и рисков имеет вид
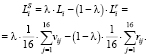 (19)
(19)
Лучшим вариантом долевого участия 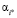 будет альтернатива:
будет альтернатива:
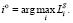 (20)
(20)
Параметр λ∈[0; 1] характеризует значимость для инвестора выигрышей при выборе наилучшего инвестиционного решения. Соответственно, параметр (1 – λ) характеризует значимость информации о рисках.
Таблица 12
Выбор лучшей альтернативы по синтетическому критерию Лапласа
|
Li |
|
|||
|
Долевое участие |
α1 |
1.00 |
12.50 |
9.30 |
|
α2 |
0.75 |
11.42 |
10.38 |
|
|
α3 |
0.50 |
10.34 |
11.46 |
|
|
α4 |
0.30 |
9.47 |
12.33 |
|
|
α5 |
0.10 |
8.61 |
13.19 |
|
|
α6 |
0.00 |
8.18 |
13.63 |
|
Наилучшие оценки эффективности решений по критериям Лапласа относительно выигрышей и относительно рисков указывают на приоритетность альтернативы α1 = 1 (табл. 12). Из этого следует, что при любых весовых коэффициентах λ и (1 – λ) лучшей альтернативой по синтетическому критерию Лапласа будет α1 = 1.
Это значит, что по синтетическому критерию Лапласа оптимальным решением является 100 % финансирование инвестиционного проекта и отказ от приобретения финансовых активов при любых весовых коэффициентах выигрышей λ и рисков (1 – λ).
Критерий Ходжа – Лемана относительно выигрышей
ЛПР, применяющий критерий Ходжа – Лемана, относится с неполным доверием к оценкам вероятностей возможных сценариев развития событий. Показатель доверия к вероятностному распределению возможных сценариев принимает значения в интервале от нуля до единицы:
γ∈[0; 1].
Эффективность долевого участия αi по критерию Ходжа – Лемана оценивается по формуле
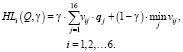 (21)
(21)
Лучшим вариантом долевого участия 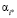 будет альтернатива:
будет альтернатива:
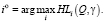 (22)
(22)
Определить точное значение показателя доверия γ для ЛПР практически невозможно. Однако можно выделить интервалы значений показателя доверия, которым соответствуют различные оптимальные варианты решений. Найдем оценки эффективности вариантов долевого участия в инвестиционном проекте по критерию Ходжа – Лемана, перебирая все возможные значения параметра γ с шагом 0,1 (табл. 13).
Таблица 13
Эффективность вариантов долевого участия в инвестиционном проекте по критерию Ходжа – Лемана
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|||
|
Долевое участие |
α1 |
1.00 |
-35.0 |
-28.1 |
-21.2 |
-14.3 |
-7.5 |
-0.6 |
6.3 |
13.2 |
20.1 |
27.0 |
33.8 |
|
α2 |
0.75 |
-27.8 |
-22.1 |
-16.5 |
-10.8 |
-5.2 |
0.4 |
6.1 |
11.7 |
17.4 |
23.0 |
28.6 |
|
|
α3 |
0.50 |
-20.5 |
-16.1 |
-11.7 |
-7.3 |
-2.9 |
1.5 |
5.9 |
10.2 |
14.6 |
19.0 |
23.4 |
|
|
α4 |
0.30 |
-14.7 |
-11.3 |
-7.9 |
-4.5 |
-1.1 |
2.3 |
5.7 |
9.1 |
12.5 |
15.9 |
19.3 |
|
|
α5 |
0.10 |
-8.9 |
-6.5 |
-4.1 |
-1.7 |
0.7 |
3.1 |
5.5 |
7.9 |
10.3 |
12.7 |
15.1 |
|
|
α6 |
0.00 |
-6.0 |
-4.1 |
-2.2 |
-0.3 |
1.6 |
3.5 |
5.4 |
7.3 |
9.2 |
11.1 |
13.0 |
|
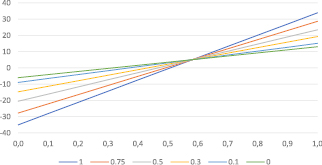
Рис. 2. Альтернативные варианты долевого участия по критерию Ходжа – Лемана
Для нахождения интервалов доверия к вероятностям сценариев представим графически оценки эффективности альтернативных вариантов долевого участия (рис. 2).
Верхняя огибающая отрезков на графике (рис. 2) соответствует максимальным выигрышам ЛПР при различных величинах степени доверия к распределению вероятностей сценариев развития событий. Точка пересечения отрезков, образующих верхнюю огибающую, находится из уравнения
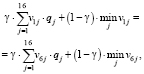 (23)
(23)
γ•33,835 + (1 – γ)•(–35) = γ•13 + (1 – γ)•(–6)
γ = 0,58.
Таким образом, согласно критерию Ходжа – Лемана лучшими решениями инвестора являются:
- отказ от финансирования инвестиционного проекта и приобретение финансовых активов компании α6 = 0 при γ∈[0; 0,58];
- отказ от финансовых инвестиций и 100 % финансирование инвестиционного проекта α1 = 1 при γ∈[0,58; 1].
При γ = 0,58 все альтернативные решения по критерию Ходжа – Лемана равноценны.
Синтетический критерий Гермейера оптимальности решений относительно выигрышей и рисков
Выбирая альтернативу αi, инвестор получит выигрыш vij, если события будут развиваться по сценарию j. Вероятность этого сценария равна qj. Соответственно, и выигрыш vij инвестор получит с вероятностью qj.
При использовании критерия Гермейера количественной характеристикой выигрыша является величина (vij•qj). Анализируя эффективность принятия решений, ЛПР сравнивает взвешенные выигрыши, учитывая вероятности их получения.
Из элементов (vij•qj) формируется матрица Гермейера:
 (24)
(24)
В рассматриваемой задаче m = 6, n = 16.
Применяя критерий Гермейера относительно выигрышей, ЛПР оценивает эффективность Gi решения αi по гарантированному взвешенному выигрышу, т.е.
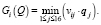 (25)
(25)
Лучшим решением будет альтернатива 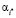 с наибольшим показателем эффективности:
с наибольшим показателем эффективности:
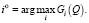 (26)
(26)
Применение критерия Гермейера относительно рисков предполагает построение матрицы:
 (27)
(27)
Таблица 14
Матрица Гермейера задачи оптимального распределения инвестиций
|
Матрица Гермейера |
Сценарии развития событий |
|||||||||||||||||
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
S8 |
S9 |
S10 |
S11 |
S12 |
S13 |
S14 |
S15 |
S16 |
|||
|
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
R8 |
R9 |
R10 |
R11 |
R12 |
R13 |
R14 |
R15 |
R16 |
|||
|
0.16 |
0.16 |
0.16 |
-0.05 |
0.16 |
0.16 |
-0.05 |
-0.05 |
0.16 |
0.16 |
-0.05 |
-0.05 |
0.16 |
-0.05 |
-0.05 |
-0.05 |
|||
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
V16 |
|||
|
180 |
170 |
165 |
160 |
155 |
145 |
140 |
135 |
130 |
125 |
120 |
110 |
105 |
100 |
95 |
85 |
|||
|
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
q7 |
q8 |
q9 |
q10 |
q11 |
q12 |
q13 |
q14 |
q15 |
q16 |
|||
|
0.162 |
0.108 |
0.243 |
0.054 |
0.018 |
0.162 |
0.036 |
0.081 |
0.027 |
0.012 |
0.006 |
0.054 |
0.018 |
0.004 |
0.009 |
0.006 |
|||
|
Матрица Гермейера относительно выигрышей |
||||||||||||||||||
|
Долевое участие |
α1 |
1.00 |
9.72 |
5.40 |
10.94 |
2.16 |
0.63 |
4.05 |
0.72 |
1.22 |
0.27 |
0.06 |
0.00 |
-0.54 |
-0.27 |
-0.08 |
-0.23 |
-0.21 |
|
α2 |
0.75 |
8.07 |
4.57 |
9.37 |
1.54 |
0.56 |
3.82 |
0.49 |
0.79 |
0.33 |
0.10 |
-0.01 |
-0.49 |
-0.12 |
-0.04 |
-0.18 |
-0.17 |
|
|
α3 |
0.50 |
6.42 |
3.74 |
7.80 |
0.92 |
0.49 |
3.58 |
0.25 |
0.36 |
0.39 |
0.15 |
-0.02 |
-0.43 |
0.04 |
0.00 |
-0.14 |
-0.12 |
|
|
α4 |
0.30 |
5.09 |
3.07 |
6.55 |
0.42 |
0.43 |
3.39 |
0.06 |
0.02 |
0.44 |
0.18 |
-0.03 |
-0.39 |
0.16 |
0.03 |
-0.11 |
-0.09 |
|
|
α5 |
0.10 |
3.77 |
2.41 |
5.29 |
-0.08 |
0.37 |
3.20 |
-0.12 |
-0.32 |
0.49 |
0.21 |
-0.03 |
-0.35 |
0.28 |
0.06 |
-0.07 |
-0.05 |
|
|
α6 |
0.00 |
3.11 |
2.07 |
4.67 |
-0.32 |
0.35 |
3.11 |
-0.22 |
-0.49 |
0.52 |
0.23 |
-0.04 |
-0.32 |
0.35 |
0.08 |
-0.05 |
-0.04 |
|
|
Матрица Гермейера относительно рисков |
||||||||||||||||||
|
Долевое участие |
α1 |
1.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.25 |
0.17 |
0.00 |
0.22 |
0.62 |
0.16 |
0.17 |
0.17 |
0.00 |
|
α2 |
0.75 |
0.83 |
1.57 |
0.62 |
0.07 |
0.23 |
0.23 |
0.43 |
0.19 |
0.13 |
0.01 |
0.16 |
0.46 |
0.12 |
0.13 |
0.13 |
0.83 |
|
|
α3 |
0.50 |
1.66 |
3.13 |
1.24 |
0.14 |
0.47 |
0.47 |
0.85 |
0.12 |
0.09 |
0.02 |
0.11 |
0.31 |
0.08 |
0.09 |
0.09 |
1.66 |
|
|
α4 |
0.30 |
2.33 |
4.39 |
1.74 |
0.20 |
0.66 |
0.66 |
1.19 |
0.07 |
0.05 |
0.03 |
0.06 |
0.18 |
0.05 |
0.05 |
0.05 |
2.33 |
|
|
α5 |
0.10 |
2.99 |
5.64 |
2.24 |
0.26 |
0.85 |
0.84 |
1.53 |
0.02 |
0.02 |
0.03 |
0.02 |
0.06 |
0.02 |
0.02 |
0.02 |
2.99 |
|
|
α6 |
0.00 |
3.33 |
6.27 |
2.48 |
0.28 |
0.94 |
0.94 |
1.70 |
0.00 |
0.00 |
0.04 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
3.33 |
|
Применяя критерий Гермейера относительно рисков, ЛПР оценивает неэффективность Gi решения αi по максимальному из возможных взвешенных рисков, т.е.
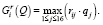 (28)
(28)
Лучшим решением будет альтернатива 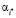 с наименьшим показателем риска:
с наименьшим показателем риска:
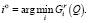 (29)
(29)
Показатель эффективности по синтетическому критерию Гермейера относительно выигрышей и рисков имеет вид
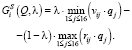 (30)
(30)
Параметр λ∈[0; 1] характеризует значимость взвешенных выигрышей при сравнении альтернатив.
Матрицы Гермейера относительно выигрышей и рисков представлены в табл. 14.
Лучшим решением будет альтернатива 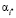 с максимальным показателем эффективности
с максимальным показателем эффективности 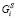 :
:
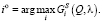 (31)
(31)
Оценки эффективности Gi и неэффективности 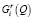 приведены в табл. 15. Оценки эффективности альтернатив по синтетическому критерию Гермейера при различных значениях параметра λ содержит табл. 16.
приведены в табл. 15. Оценки эффективности альтернатив по синтетическому критерию Гермейера при различных значениях параметра λ содержит табл. 16.
Таблица 15
Выбор лучшей альтернативы по критерию Гермейера
|
Gi(Q) |
|
|||
|
Долевое участие |
α1 |
1.00 |
-0.54 |
0.62 |
|
α2 |
0.75 |
-0.49 |
1.65 |
|
|
α3 |
0.50 |
-0.43 |
3.30 |
|
|
α4 |
0.30 |
-0.39 |
4.63 |
|
|
α5 |
0.10 |
-0.35 |
5.95 |
|
|
α6 |
0.00 |
-0.49 |
6.61 |
|
Таблица 16
Эффективность вариантов долевого участия в инвестиционном проекте по синтетическому критерию Гермейера
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|||
|
Долевое участие |
α1 |
1.00 |
-0.62 |
-0.61 |
-0.60 |
-0.59 |
-0.59 |
-0.58 |
-0.57 |
-0.56 |
-0.56 |
-0.55 |
-0.54 |
|
α2 |
0.75 |
-1.65 |
-1.54 |
-1.42 |
-1.30 |
-1.19 |
-1.07 |
-0.95 |
-0.84 |
-0.72 |
-0.60 |
-0.49 |
|
|
α3 |
0.50 |
-3.30 |
-3.02 |
-2.73 |
-2.44 |
-2.16 |
-1.87 |
-1.58 |
-1.29 |
-1.01 |
-0.72 |
-0.43 |
|
|
α4 |
0.30 |
-4.63 |
-4.20 |
-3.78 |
-3.36 |
-2.93 |
-2.51 |
-2.08 |
-1.66 |
-1.24 |
-0.81 |
-0.39 |
|
|
α5 |
0.10 |
-5.95 |
-5.39 |
-4.83 |
-4.27 |
-3.71 |
-3.15 |
-2.59 |
-2.03 |
-1.47 |
-0.91 |
-0.35 |
|
|
α6 |
0.00 |
-6.61 |
-6.00 |
-5.38 |
-4.77 |
-4.16 |
-3.55 |
-2.94 |
-2.32 |
-1.71 |
-1.10 |
-0.49 |
|
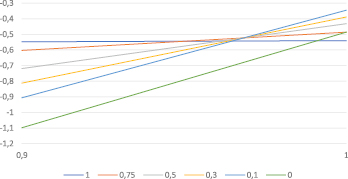
Рис. 3. Альтернативные варианты долевого участия по синтетическому критерию Гермейера
Графическое представление альтернативных решений по синтетическому критерию Гермейера для диапазона λ∈[0,9; 1] представлено на рис. 3.
Верхняя огибающая отрезков на рис. 3 соответствует максимальным выигрышам ЛПР при различных величинах параметра λ и включает альтернативы α1 = 1, α2 = 0,75 и α5 = 0,1.
Таблица 19
Эффективность вариантов долевого участия в инвестиционном проекте по критерию Гермейера – Гурвица
|
Количественная мера оптимизма ЛПР |
|||||||||||||
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|||
|
Долевое участие |
α1 |
1.00 |
-0.54 |
0.61 |
1.76 |
2.90 |
4.05 |
5.20 |
6.35 |
7.49 |
8.64 |
9.79 |
10.94 |
|
α2 |
0.75 |
-0.49 |
0.50 |
1.48 |
2.47 |
3.46 |
4.44 |
5.43 |
6.41 |
7.40 |
8.38 |
9.37 |
|
|
α3 |
0.50 |
-0.43 |
0.39 |
1.21 |
2.04 |
2.86 |
3.68 |
4.51 |
5.33 |
6.15 |
6.98 |
7.80 |
|
|
α4 |
0.30 |
-0.39 |
0.30 |
1.00 |
1.69 |
2.39 |
3.08 |
3.77 |
4.47 |
5.16 |
5.85 |
6.55 |
|
|
α5 |
0.10 |
-0.35 |
0.22 |
0.78 |
1.35 |
1.91 |
2.47 |
3.04 |
3.60 |
4.16 |
4.73 |
5.29 |
|
|
α6 |
0.00 |
-0.49 |
0.03 |
0.54 |
1.06 |
1.57 |
2.09 |
2.60 |
3.12 |
3.64 |
4.15 |
4.67 |
|
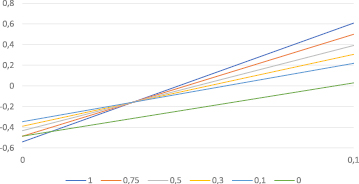
Рис. 4. Альтернативные варианты долевого участия по критерию Гермейера – Гурвица
Точка пересечения отрезков λ1, соответствующих альтернативам α1 = 1 и α2 = 0,75, находится из уравнения
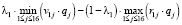
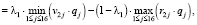 (32)
(32)
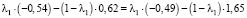
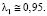
Точку пересечения отрезков λ2, соответствующих альтернативам α2 = 0,75 и α5 = 0,1, найдем из уравнения:
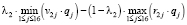
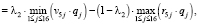 (32)
(32)
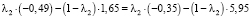
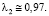
Таким образом, по синтетическому критерию Гермейера лучшими решениями инвестора являются:
- отказ от финансовых инвестиций и 100 % финансирование инвестиционного проекта α1 = 1 при λ∈[0; 0,95];
- долевое участие в проекте α2 = 0,75 при λ∈[0,95; 0,97];
- долевое участие в проекте α5 = 0,1 при λ∈[0,97; 1].
Таким образом, доминирующей альтернативой при любом λ∈[0; 0,95] является решение α1 = 1. В этом случае ЛПР учитывает риски с весом не менее 5 %.
Приоритетность решения α1 = 1 подтверждает также решение задачи методом идеальной точки (табл. 17). Минимальное расстояние до идеальной точки соответствует решению о 100 % финансировании инвестиционного проекта и одновременном отказе от инвестиций в финансовые активы компании.
Таблица 17
Выбор лучшей альтернативы по методу идеальной точки
|
Gi(Q) |
|
di(Q) |
|||
|
Долевое участие |
α1 |
1.00 |
-0.54 |
0.62 |
0.04 |
|
α2 |
0.75 |
-0.49 |
1.65 |
1.09 |
|
|
α3 |
0.50 |
-0.43 |
3.30 |
7.24 |
|
|
α4 |
0.30 |
-0.39 |
4.63 |
16.09 |
|
|
α5 |
0.10 |
-0.35 |
5.95 |
28.44 |
|
|
6 |
0.00 |
-0.49 |
6.61 |
35.95 |
|
|
Идеальная точка |
-0,35 |
0,62 |
|||
Критерий Гермейера – Гурвица оптимальности решений относительно выигрышей
Критерий Гермейера – Гурвица позволяет смягчить крайние пессимистические представления ЛПР о сценариях развития событий при применении критерия Гермейера благодаря возможности выбора показателя оптимизма β∈[0; 1].
Показателем эффективности решения αi по критерию Гермейера – Гурвица относительно выигрышей является число
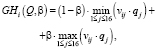 (34)
(34)
или
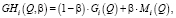 (35)
(35)
где
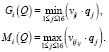 (36)
(36)
Лучшим решением будет альтернатива 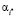 с наибольшим показателем эффективности GHi(Q, β):
с наибольшим показателем эффективности GHi(Q, β):
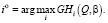 (37)
(37)
Оценки эффективности Gi по классическому критерию Гермейера и оценки эффективности Mi по критерию максимакса приведены в табл. 18.
Параметр β∈[0; 1] выражает количественную меру оптимизма ЛПР, т.е. меру его уверенности в наилучшем развитии событий. Соответственно, число (1 – β) характеризует степень уверенности ЛПР в наихудшем развитии событий.
Далее будем предполагать, что ЛПР способен сделать выбор оптимальной альтернативы αi, основываясь на интервалах значений параметра β и соответствующих им лучших решениях.
Таблица 18
Выбор лучшей альтернативы по критерию Гермейера – Гурвица
|
Gi(Q) |
Mi(Q) |
|||
|
Долевое участие |
α1 |
1.00 |
-0.54 |
10.94 |
|
α2 |
0.75 |
-0.49 |
9.37 |
|
|
α3 |
0.50 |
-0.43 |
7.80 |
|
|
α4 |
0.30 |
-0.39 |
6.55 |
|
|
α5 |
0.10 |
-0.35 |
5.29 |
|
|
α6 |
0.00 |
-0.49 |
4.67 |
|
Графическое представление наилучших решений по критерию Гермейера – Гурвица для диапазона β∈[0; 0,1] представлено на рис. 4. Графики построены на основании данных в табл. 19.
Верхняя огибающая отрезков на рис. 4 соответствует максимальным взвешенным выигрышам ЛПР при различных величинах параметра β и включает альтернативы α5 = 0,1, α1 = 1.
Точка пересечения отрезков, соответствующих альтернативам α5 = 0,1 и α1 = 1, находится из уравнения
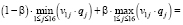 (38)
(38)
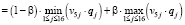
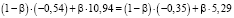
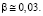
Таким образом, по критерию Гермейера – Гурвица лучшими решениями инвестора являются:
- финансирование инвестиционного проекта в доле α5 = 0,1 при β∈[0; 0,03];
- финансирование инвестиционного проекта в доле α1 = 1 при β∈ [0,03; 1].
Так как величина β в точке пересечения графиков доминирующих альтернатив близка к нулю, малым отрезком [0; 0,03] можно пренебречь. Это значит, что лучшим решением инвестора по критерию Гермейера – Гурвица является 100 % финансирование инвестиционного проекта и отказ от финансовых инвестиций.
Таблица 20
Результаты решения задачи оптимизации распределения инвестиций
|
Критерий |
Оптимальное инвестиционное решение |
|
Критерий Байеса и метод идеальной точки |
α2 = 0.75 |
|
Синтетический критерий Байеса |
α1 = 1 |
|
Критерий Лапласа и метод идеальной точки |
α4 = 0.3 |
|
Синтетический критерий Лапласа |
α1 = 1 |
|
Критерий Ходжа-Лемана |
α6 = 0при γ∈[0; 0.58], α1 = 1 при γ∈[0.58; 1] |
|
Синтетический критерий Гермейера |
α1 = 1 при λ∈[0; 0.95], α2 = 0.75 при λ∈[0.95; 0.97], α5 = 0.1 при λ∈[0.97; 1] |
|
Критерий Гермейера-Гурвица |
α5 = 0.1 при β∈[0; 0.03], α1 = 1 при β∈[0.03; 1] |
Заключение
В статье изложены подходы к анализу эффективности распределения инвестиций в рамках игры с природой с применением критериев Байеса, Лапласа, Ходжа – Лемана, Гермейера и их модификаций. Для реализации многокритериальности сравнительной оценки альтернатив применен метод идеальной точки и привлечены также некоторые комбинированные критерии принятия решений: критерий Ходжа – Лемана, синтетические критерии Байеса, Лапласа, Гермейера, а также критерий Гермейера – Гурвица. Многокритериальность оценки основывается на взвешенном анализе выигрышей и рисков ЛПР. В основу комбинированных критериев оптимальности заложены показатели выигрышей и рисков (синтетические критерии оптимальности), показатели выигрышей с учетом степени доверия ЛПР к оценкам вероятностей и его отношения к риску (критерий Ходжа – Лемана), показатели выигрышей с учетом степени уверенности ЛПР в получении наилучших взвешенных результатов (критерий Гермейера – Гурвица).
В результате решения задачи оптимального распределения инвестиций были получены следующие результаты (табл. 20).
Материал статьи может быть полезен специалистам-практикам и может быть положен в основу методики многофакторного и многокритериального отбора альтернатив. Практическая задача, изложенная в статье, может быть уточнена, а соответствующая задаче модель модифицирована с учетом специфики факторов, определяющих развитие событий и вероятностей их благоприятного проявления. Изложенные в статье математические инструменты принятия решений предназначены для поддержки принятия решений. Основное их назначение – формализованный сравнительный анализ альтернативных инвестиционных решений, позволяющий выделить наиболее приоритетные альтернативы.