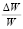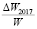Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Привлекательность проживания в том или ином регионе в представлении людей, как правило, в первую очередь связывается с возможностью найти работу с высоким заработком. Величина заработной платы, наличие рабочих мест, условия проживания определяют перераспределение человеческих ресурсов внутри страны, поэтому моделированию существующих взаимосвязей названных факторов в научной литературе уделяется особое внимание.

Первой и самой известной моделью, исследующей зависимость заработной платы (прироста) и уровня безработицы, является кривая Филлипса. На основе данных по Великобритании 1861–1957 гг. Филлипс подтвердил существование нелинейной зависимости между рассматриваемыми показателями. Исходные предположения, положенные в основу модели, критика и дальнейшее развитие теории в зарубежных исследованиях последовательно и подробно описаны в труде Эрнста Берндта [1]. Однако, на наш взгляд, большой интерес представляет и то, как моделируется взаимосвязь между данными показателями отечественными учеными на российских данных.

Целью исследования стало описание математических моделей, применяемых в отечественной практике для исследования зависимости между заработной платой и безработицей, а также создание комбинированной спецификации и ее оценка на основе региональной статистики, публикуемой Росстатом.

Материалы и методы исследования

В современной российской практике изучение зависимости между данными показателями проходит в рамках различных подходов.

Разделим их условно на пять основных типов:

1) развитие концепции кривой Филлипса;

2) построение моделей на основе теории компенсирующих различий;

3) исследования базовых механизмов рынка труда;

4) косвенные методы, моделирующие спрос и предложение труда;

5) косвенные методы, моделирующие связь безработицы и минимальной заработной платы; безработицы и среднедушевых денежных доходов.

Опишем каждый из перечисленных типов.

Подход 1 – развитие концепции кривой Филлипса

Данный подход встречается в работах [2; 3]. В частности, в работе Белявского М.О., Коровкина А.Г., Полежаева А.В. [2] на базе ежемесячных данных по Российской Федерации, охватывающих период с мая 1994 по апрель 2000 г., оценивались регрессионные модели, основой для построения которых, как отмечают авторы, послужила концепция кривой Филлипса.

Исходная модель (модель 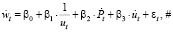1):

(1)

где 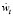– темп прироста номинальной заработной платы, ut – уровень безработицы,

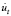– темп прироста уровня безработицы, 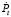– темп прироста потребительских цен,

β_j, j = 0,…,3 – коэффициенты модели, ε_t – случайное возмущение.

Также в работе [2] исследуется скорректированная модель (модель 2):

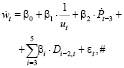(3)

где D1, D2, D3 – фиктивные переменные, учитывающие колебания темпа прироста номинальной заработной платы.

Оценка модели (1) и модели (3) дает β1 > 0.

Для прогноза численности безработных в статье использованы различные модели, среди которых одна содержит темп прироста номинальной зарплаты в качестве регрессора:

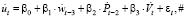(4)

где 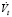– месячный темп прироста вакансий.

В данной модели оценка β1 < 0.

Во второй работе Коровкина А.Г., Подорвановой Ю.А., Долговой И.Н. [3] на основе региональных ежемесячных данных, охватывающих период с марта 1994 по декабрь 2001 г., оценивались регрессии для субъектов РФ (для каждого отдельно) с исходной спецификацией:

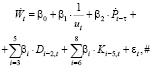(5)

где 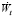– темп прироста номинальной заработной платы, ut – уровень безработицы,

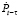– темп прироста потребительских цен с лагом τ мес., D1, D2, D3, K1, K2, K3 – фиктивные переменные, отражающие всплески и падения номинальной заработной платы в различных месяцах/кварталах, β_j, j = 0,…,8 – параметры модели, ε_t – регрессионная ошибка.

Для каждого региона был выполнен поиск наиболее адекватной модификации приведенного уравнения посредством оценивания с различными комбинациями переменных. Следует отметить, что описательная способность по округам оказалась выше, чем по отдельным регионам, а по России в целом получен наибольший показатель детерминации.

Анализ оцененных моделей выявил, что влияние роста цен на изменение номинальной зарплаты – запаздывающее, а воздействие уровня безработицы на динамику зарплаты по регионам – неоднозначное: были выявлены субъекты, в которых связь данных показателей статистически незначима (в частности, все регионы Дальнего Востока и некоторые регионы Восточной Сибири).

Подход 2 – использование теории компенсирующих различий

Данная теория основывается на том, что в заработной плате присутствует часть, которая компенсирует неблагоприятные условия проживания в регионе [4]. В частности, Ощепков А.Ю. [5; 6] исследовал межрегиональные различия в оплате труда на основе следующей спецификации:

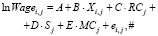(6)

где Wagei,j – заработная плата работника i из региона j,

X – набор характеристик работников и рабочих мест, отражающих региональную структуру занятости, RC – набор региональных характеристик, S – набор переменных, контролирующих воздействие экономических шоков на межрегиональную структуру заработных плат, MC – переменные, отражающие издержки миграции, A, B, C, D, E – коэффициенты, e – случайное возмущение.

Для оценки (6) использовалась информация Росстата и Национального обследования бюджетов домашних хозяйств и участия в социальных программах (НОБУС, 2003).

В набор (X) благодаря данным НОБУС вошли такие показатели, как пол работника, его возраст, квадрат возраста, уровень образования, стаж работы на предприятии, отраслевая принадлежность, фактическая продолжительность рабочего времени, профессиональный статус и др. Набор региональных характеристик (RC) – это агрегированные региональные показатели, публикуемые Росстатом. В частности, стоимость фиксированного набора товаров и услуг использовалась для измерения издержек проживания в субъекте; а в состав неденежных аспектов проживания вошли такие характеристики, как средняя температура января, средняя ожидаемая продолжительность жизни при рождении, число зарегистрированных преступлений (на 100 тыс. населения), численность медицинского персонала (на 10 тыс. жителей), количество автобусов (на 100 тыс. жителей), плотность автодорог с асфальтовым покрытием, оснащенность квартирными телефонными аппаратами, интенсивность выбросов загрязняющих веществ, уровень региональной безработицы, близость региона к конфликту в Чеченской Республике. Набор (S) включает две переменные, которые рассчитывались на основе данных Росстата о ВВП и ВРП, для учета влияния шоков. Для отражения величины издержек миграции (MC) была выбрана прокси-переменная – расстояние от административного центра субъекта до Москвы. Автор исходит из того, что указанная переменная удаленности от федеральной столицы может отражать разницу в транспортных и информационных издержках.

Согласно выводам исследования [5], работники получают компенсацию, во-первых, за более высокий уровень цен, во-вторых, за сравнительно неблагоприятную среду проживания (в частности, более холодный климат, низкую ожидаемую продолжительность жизни, низкую обеспеченность медицинским персоналом, неблагополучную экологическую обстановку). Наибольший вклад в вариацию региональных заработных плат вносит уровень цен. Компенсируется также и более высокий уровень безработицы, но коэффициент при данном показателе слабо значим.

К данному подходу также отнесем работу Гильтман М.А. [4]. На региональных данных (северные регионы) за 2005–2013 гг. были построены и оценены эконометрические модели с фиксированными эффектами. Три модели отличались выбранной эндогенной переменной: в первой зависимой переменной выступала численность занятых, во второй – численность безработных, в третьей – сальдо миграции. Факторами являлись номинальная начисленная заработная плата, дефлированная к ценам 2005 г., доли занятых в торговле, строительстве и обрабатывающей промышленности, доля населения в трудоспособном возрасте, количество женщин, приходящихся на 1000 мужчин, ВРП, ожидаемая продолжительность жизни при рождении, среднее время поиска работы безработными. Значимым фактором для объяснения численности безработных стала только заработная плата (текущего года и с лагом 5 лет).

Подход 3 – исследование базовых механизмов российского рынка труда

В работе Вакуленко Е.С., Гурвич Е.Т. [7] были исследованы базовые механизмы российского рынка труда; изучалась взаимосвязь трех основных агрегированных характеристик: реальной величины заработной платы, уровня безработицы и производительности труда. Исходными данными выступали квартальные значения показателей в период с начала 1995 по 3 квартал 2013 г. Взаимосвязь исследуемых переменных оценивалась с помощью векторных моделей авторегрессии. Использовалась векторная модель коррекции ошибок, а также были рассмотрены векторные модели коррекции ошибок с асимметрией.

Приведем некоторые полученные результаты: уровень безработицы реагирует сильнее на уменьшение реальной заработной платы, чем на увеличение; после шоков безработица возвращается к своему долгосрочному тренду; подстройка к долгосрочному соотношению не имеет значимой асимметрии. Из коинтеграционных уравнений следует: зарплата отрицательно зависит от уровня безработицы и положительно – от производительности труда.

Подход 4 – косвенные методы (моделирование спроса и предложения труда)

Данные модели названы косвенными, потому что не моделируют напрямую связь заработной платы и безработицы. Например, в работе Гильтман М.А. [8] было построено и оценено регрессионное уравнение предложения труда в регионах. В качестве эндогенной переменной выступал логарифм численности экономически активного населения (ЭАН), а значимыми факторами были признаны логарифм средней заработной платы в регионе, доля населения в трудоспособном возрасте в ЭАН, а также логарифм плотности населения региона. Оценка коэффициента при логарифме зарплат получилась меньше нуля.

В работе Гильтман М.А., Вотяковой А.А. [9] для выявления факторов, влияющих на динамику занятости в регионах, на панельных данных за 2006–2012 гг. для 79 субъектов РФ оценивалась модель с фиксированными эффектами. Зависимой переменной выступал логарифм численности занятых, независимыми переменными являлись логарифм ВРП в ценах 2006 г. (текущие значения и с лагами до 5 лет), логарифм заработной платы в ценах 2006 г. (текущие значения и с лагами до 3 лет), логарифмы структурных составляющих – доли занятых в обрабатывающей промышленности и сельском хозяйстве – с лагами до 5 и 4 лет соответственно. Статистически значимым оказалось только влияние ВРП (текущего года и с лагом 5 лет).

Подход 5 – изучение связи безработицы и минимальной заработной платы/доходов

Данные модели также можно назвать косвенными, потому что моделируется влияние изменений в минимальной заработной плате (МЗП) и среднедушевых денежных доходах. Исследованию подобных зависимостей посвящены работы [10–13].

В работе [10] построены модели, в которых в качестве эндогенной переменной рассматривается размер минимальной заработной платы. Первая модель – линейная регрессия:

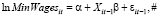(6)

где α, β – коэффициенты модели, MinWages_it – номинальная минимальная зарплата занятых во внебюджетном секторе.

В качестве независимых переменных выбран широкий круг факторов: 4 социально-демографических, 1 климатический, 1 политический, 8 экономических, в том числе уровень фактической безработицы. Также применялись пробит-модели, цензурированная регрессия, порядковая логит-модель. Для оценки моделей использовались данные за 2008–2011 гг. Все модели оценивались отдельно за каждый год.

В статье [11] автор развивает описанный подход, оценивая модель не отдельно для каждого года, а по всем имеющимся данным, т.е. по панели. Первая оцениваемая модель – с фиксированными эффектами, вторая – с лаговой зависимой переменной, третья – пробит-модель. В расширенной спецификации к описанным ранее факторам добавились фиктивные переменные для 10 природно-климатических зон.

Данный сегмент моделей представлен и в виде простых моделей парной регрессии, например [12], и множественной регрессии [13]. В работе Коокуевой В.В. [12] за 2000–2015 годы были построены парные корреляционно-регрессионные модели, в которых в качестве регрессора выступал МРОТ, в качестве зависимой переменной – численность безработных или уровень безработицы. Расчеты выполнялись в целом по стране и по отдельным регионам. В работе Бакушевой Г.В. [13] на данных 2017 г. по 82 субъектам РФ оценена спецификация множественной регрессионной модели, в которой зависимой переменной является уровень безработицы, а регрессорами выступали 9 факторов, среди них среднедушевые денежные доходы населения, среднее время поиска работы безработными, потребность в работниках, заявленная работодателями, охват детей дошкольным образованием и др.

Построим комбинированную модель, используя подходы 1 и 2, т.е. регрессию (1) и спецификацию теории компенсирующих различий (6). Анализ будем проводить на пространственной выборке, в качестве данных используем значения показателей по 82 регионам (исключая автономные округа) за 2018 г. (последний опубликованный на сайте Росстата, дата обращения: 10 июня 2020 г.).

Поскольку в первом подходе в качестве эндогенной переменной выступает темп прироста номинальной зарплаты, во втором – натуральный логарифм среднемесячной зарплаты, а в третьем – средняя номинальная зарплата в постоянных ценах, то сначала требуется решить вопрос о выборе зависимой переменной. Согласно пояснениям, изложенным Берндтом Э.Р. [1, с. 161], данные по заработным платам обычно асимметричны, поэтому исследователи зачастую применяют логнормальное, «скошенное», распределение. Асимметричность данных по заработным платам находит свое подтверждение и в российских исследованиях, в частности, согласно работе Дарманяна А.П. [14], среднемесячная номинальная заработная плата по субъектам РФ в 2011 г. не являлась нормально распределенной. Была выполнена проверка на нормальность эмпирического распределения среднемесячной номинальной начисленной заработной платы работников организаций (W), натурального логарифма данного показателя (ln W) и его темпов прироста в действующих ценах 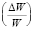и ценах 2017 г. 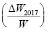. Перевод в цены 2017 г. осуществлялся дефлированием на ИПЦ.

Расчеты выполнялись в RStudio c помощью критерия Шапиро-Уилка. Результаты расчетов приведены в таблице.

Проверка нормальности распределения предполагаемых эндогенных переменных тестом Шапиро-Уилка для уровня значимости α = 0,05

Как видно из таблицы, нет оснований отвергнуть гипотезу о нормальности только в случае темпов прироста номинальной заработной платы (p – value > 0,05). Если задаваться целью получения нормального распределения зависимой переменной, то следует выбрать темп прироста. Однако если такая задача не стоит, то следует опереться на согласованность оценок получаемых связей с экономической теорией. Окончательный выбор в пользу той или иной эндогенной переменной сделаем на основе диаграмм рассеяния (рис. 1–3).

На рис. 1 и 2 четко прослеживается обратная зависимость между показателями. Таким образом, невзирая на то что асимметричность распределения была преодолена именно на темпах прироста, в качестве эндогенной переменной для пространственной выборки данный показатель, вероятно, не следует использовать, так как нарушается предполагаемый экономический смысл связи – из рис. 3 видно, что большему уровню безработицы соответствует большее значение прироста заработной платы.

Несмотря на то что логарифмирование позволяет уменьшить количество выбросов, для дальнейшего исследования в качестве эндогенной переменной выберем среднемесячную номинальную начисленную заработную плату работников организаций (W) в 2018 г., поскольку удалось найти фактор, соответствующий подобному поведению переменной. Оказалось, что у регионов с экстремально большими значениями средней номинальной зарплаты, выходящими за внешние границы Тьюки, – г. Москва, Магаданская и Сахалинская области, Камчатский край, Чукотский автономный округ – стоимость фиксированного набора товаров и услуг также имеет значения, которые диагностируются как выбросы.

Создадим набор потенциальных регрессоров, объединив факторы модели (1) и (6), заменяя, по возможности, индивидуальные характеристики подходящими по смыслу региональными. Полный перечень исходных факторов: величина, обратная уровню безработицы, годовой темп прироста уровня безработицы, индексы потребительских цен; удельный вес городского населения в общей численности населения, число родившихся на 1000 человек населения, число детей на 1 женщину, соотношение мужчин и женщин (на 1000 мужчин приходится женщин), средняя ожидаемая продолжительность жизни после рождения, численность врачей и среднего медицинского персонала в расчете на 10 тыс. жителей, выпуск бакалавров, специалистов, магистров, выпуск квалифицированных рабочих и служащих, валовой региональный продукт на душу населения, число малых предприятий на 10 000 человек населения, средняя температура января, уровень региональной безработицы, количество зарегистрированных преступлений в расчете на 100 тыс. населения, интенсивность выбросов загрязняющих веществ, число персональных компьютеров на 100 работников, стоимость фиксированного набора потребительских товаров и услуг, расстояние от административного центра региона до Москвы.

Анализ факторов на выбросы выявил необходимость исключения из общей выборки трех регионов: Республики Тыва (экстремальные выбросы в 6 показателях, в том числе по уровню безработицы), Республики Ингушетия (в 3 показателях – выход за внешние границы Тьюки, в том числе по уровню безработицы), Чеченской Республики (в 6 показателях – выход за внутренние границы Тьюки, в 2 – за внешние). Чукотский автономный округ выбран для контроля адекватности модели. Таким образом, обучающая выборка составила 78 регионов России.

При создании модели применялись методы анализа матрицы парных и частных коэффициентов корреляции, методы последовательного присоединения и удаления, выполненные в Excel и RStudio с критериями в виде значений скорректированных коэффициентов детерминации и информационных критериев соответственно. После исключения факторов, которые не вошли ни в одну из получаемых моделей, была составлена окончательная спецификация методом последовательного удаления.

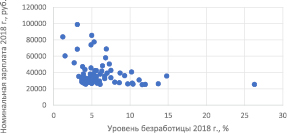
Рис. 1. Диаграмма рассеяния уровня безработицы и номинальной зарплаты в 2018 г.

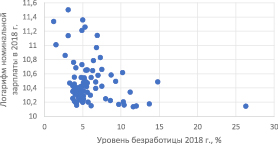
Рис. 2. Диаграмма рассеяния уровня безработицы и натурального логарифма номинальной зарплаты в 2018 г.

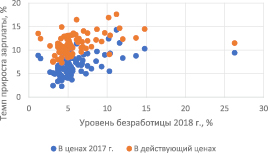
Рис. 3. Диаграмма рассеяния уровня безработицы и темпа прироста номинальной зарплаты в 2018 г.

Оценка функции регрессии итоговой модели в стандартной форме:

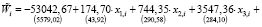
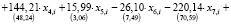
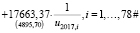(8)

где Wi – среднемесячная номинальная начисленная заработная плата работников организаций в 2018 г., руб.,

x1,i – удельный вес городского населения в общей численности населения, %,

x2,i – число родившихся на 1000 человек населения,

x3,i – стоимость фиксированного набора потребительских товаров и услуг, тыс. руб.,

x4,i – численность врачей в расчете на 10 тыс. жителей,

x5,i – валовой региональный продукт на душу населения, тыс. руб.,

x6,i – число малых предприятий на 10 тыс. человек населения,

x7,i – средняя температура января в 2014 г.,

u2017,i – уровень безработицы в 2017 г., %, i – номер региона.

Под оценками коэффициентов в формуле (8) записаны стандартные ошибки в форме Уайта. Проведенные формальные тесты подтвердили заранее предполагаемую гетероскедастичность, обусловленную различиями объектов выборки, поэтому для построения доверительных интервалов использовались устойчивые к гетероскедастичности стандартные ошибки. На основании построенных доверительных интервалов делается заключение о значимости всех включенных регрессоров в модель, а также об адекватности модели. Тестирование модели в RStudio позволяет сделать вывод, что на 5 % уровне значимости нет оснований отвергнуть гипотезы об отсутствии автокорреляции в остатках и о правильности спецификации.

Результаты исследования и их обсуждение

Полученные результаты частично совпадают с выводами модели компенсирующих различий: зарплатой компенсируются более высокий уровень цен, выражающийся в стоимости фиксированного набора товаров и услуг, и относительно неблагоприятные условия проживания – более холодному климату в среднем соответствует более высокая заработная плата.

Оценка коэффициента при переменной, обратной уровню безработицы, как и в подходе (1), получилась положительной. Согласно (8) получается, что чем больше уровень безработицы в регионе, тем меньше прибавка к заработной плате, обусловленная соответствующим слагаемым.

Также модель подтверждает, что заработные платы в городе выше, чем в сельской местности; регионы с более высоким ВРП на душу населения имеют более высокую среднюю зарплату, а малые предприятия, как правило, не имеют возможности обеспечивать высокий заработок персонала, поэтому чем больше малых предприятий, тем меньше средний уровень зарплат в регионах.

Заключение

Моделирование взаимосвязи зарплаты и уровня безработицы в российских исследованиях проводится как в рамках построения регрессионных моделей зависимости зарплаты от безработицы [2; 5], так и безработицы от зарплаты [2; 4]. Как показано в [7], результаты проверки причинности с помощью теста Грейнджера подтверждают наличие двусторонней причинно-следственной связи между показателями, поэтому оба подхода имеют право на существование. В настоящей работе в качестве зависимой переменной была выбрана заработная плата. Как показали результаты исследования, подтверждается наличие обратной связи между уровнем безработицы и номинальной заработной платой, однако установлено, что при построении модели на пространственных данных главным фактором, влияющим на эндогенную переменную, является уровень цен, представленный в виде стоимости фиксированного набора потребительских товаров и услуг.