Понятие государственного бюджета определяют как совокупность финансовых отношений, направленных на формирование органами государственной власти фондов денежных средств для удовлетворения общественных потребностей. Государственный бюджет также может быть определен как смета доходов и расходов государства, обычно за один год, с указанием источников государственных доходов и направлений расходования средств [1, с. 85]. В ситуации превышения расходов бюджета над его доходами возникает бюджетный дефицит. За период с 2010 по 2019 г. федеральный бюджет России не испытывал дефицит в 2011, 2018 и 2019 гг. (рис. 1).
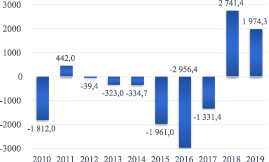
Рис. 1. Дефицит федерального бюджета в России (млрд руб.)
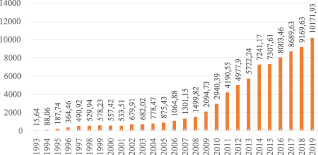
Рис. 2. Внутренний долг в России в текущих ценах (млрд руб.)
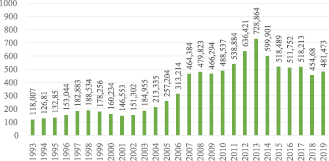
Рис. 3. Внешний долг в России (млрд долл.)
Одним из возможных источников финансирования бюджетного дефицита является денежная эмиссия. Такой способ финансирования государственного бюджета используется в случаях, когда у страны имеется значительный внутренний (рис. 2) и внешний (рис. 3) долг, при этом возможности дополнительного внутреннего и внешнего долгового финансирования практически исчерпаны [2, с. 16]. Тем не менее возможность извлечения дополнительного дохода от эмиссии денег существует и является предметом исследований ученых и специалистов в области экономики и финансов [3; 4].
Доход государства от денежной эмиссии называется сеньоражем. Сеньораж представляет собой разницу между номинальной стоимостью денег и затратами на поддержание обращения денег в экономике. На территории Российской Федерации эмиссия денег, организация их обращения и изъятия осуществляется Центральным банком РФ. Эмиссионные ресурсы передаются центральным банком правительству для временного размещения в форме кредитов и займов [5, с. 22]. Кредитный характер денежной эмиссии – один из важнейших принципов современных денежных систем.
Дополнительная денежная эмиссия, предназначенная для полного или частичного покрытия дефицита государственного бюджета, может служить причиной усиления инфляционных процессов в экономике. Прирост величины денежного предложения в экономике количественно должен быть согласован с ожидаемым увеличением темпа инфляции [6, с. 3]. Оценка оптимального темпа инфляции с точки зрения извлечения максимального дохода от эмиссии денег может быть проведена в рамках модели Фридмана эмиссионного финансирования государственного бюджета [7, с. 147–152]. В рамках модели Бруно – Фишера возможна оценка долей дефицита государственного бюджета, покрываемых дополнительной денежной эмиссией, в соответствии с инфляционными ожиданиями в обществе [7, с. 159–164].
Целью настоящего исследования является количественная оценка темпа инфляции, при котором достигается возможность извлечения максимального сеньоража в российской экономике с учетом влияния внешних дестабилизирующих факторов, а также оценка долей покрытия дефицита государственного бюджета за счет денежной эмиссии в зависимости от инфляционных ожиданий. Применяемые методы исследования – формализация и математизация проблемы количественного оценивания параметров денежной эмиссии для финансирования дефицита государственного бюджета. В статье представлен эконометрический анализ моделей Фридмана и Бруно – Фишера эмиссионного финансирования государственного бюджета. Построены соответствующие эконометрические модели с дополнительными переменными, отражающими усиление или ослабление кризисных явлений в экономике России. В исследовании рассматривается период с 1999 по 2018 г.
Модель Фридмана
Формально реальный сеньораж RS можно определить как изменение денежной массы в реальном выражении при фиксированном уровне цен 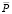 :
:
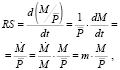 (1)
(1)
где 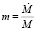 – темп прироста денежной массы,
– темп прироста денежной массы, 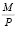 – денежная масса в реальном выражении.
– денежная масса в реальном выражении.
Эмиссия денег, обесценивая номинальную денежную единицу, равносильна введению инфляционного налога. Реальный инфляционный налог RIT – это изменение реальной денежной массы при фиксированной величине номинальной денежной массы 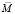 :
:
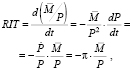 (2)
(2)
где 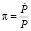 – темп инфляции. В выражении (2) темп инфляции π можно интерпретировать как ставку инфляционного налога, а реальную денежную массу
– темп инфляции. В выражении (2) темп инфляции π можно интерпретировать как ставку инфляционного налога, а реальную денежную массу 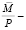 как налоговую базу.
как налоговую базу.
Учитывая предложенную интерпретацию, можно предположить, что для инфляционного налога справедлива модель Лаффера, описывающая зависимость между налоговой ставкой и налоговыми поступлениями (рис. 4).
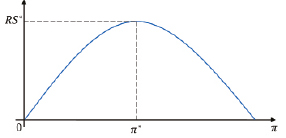
Рис. 4. Кривая Лаффера для инфляционного налога (схематичное представление)
Описанная выше идея интерпретации кривой Лаффера для инфляционного налога была положена в основу модели Милтона Фридмана. Модель позволяет оценивать темп инфляции в экономике, при котором реальный сеньораж будет максимальным.
Фридман предложил использовать для описания спроса 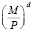 на реальные запасы денежных средств функцию вида
на реальные запасы денежных средств функцию вида
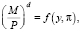 (3)
(3)
где y – реальный доход индивида, π – ожидаемый темп инфляции. В выражении (3) темп инфляции заменяет номинальную процентную ставку. В основу такой замены было положено уравнение Фишера
i = r + π, (4)
согласно которому при фиксированной реальной процентной ставке r динамика номинальной процентной ставки i с точностью до константы r совпадает с динамикой темпа инфляции.
Если выражение (3) соответствует функции спроса на деньги для отдельного индивида, то агрегированную функцию спроса на деньги можно получить, умножив (3) на численность L экономически активного населения:
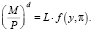 (5)
(5)
В модели предполагается равновесие рынка денег:
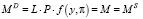 (6)
(6)
или
L•P•f = M, (7)
где Md – спрос на деньги, MS – предложение денег, M – номинальная денежная масса.
Прологарифмируем левую и правую части тождества (7) и возьмём производную по времени t:
ln L + ln P + ln f = ln M, (8)
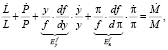 (9)
(9)
где 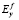 и
и 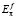 – коэффициенты эластичности спроса на реальные запасы денег по доходу индивида и темпу инфляции соответственно. С учётом обозначений, принятых в (1) и (2), перепишем выражение (9) в виде
– коэффициенты эластичности спроса на реальные запасы денег по доходу индивида и темпу инфляции соответственно. С учётом обозначений, принятых в (1) и (2), перепишем выражение (9) в виде
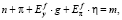 (10)
(10)
где 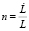 – темп прироста экономически активного населения,
– темп прироста экономически активного населения, 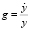 – темп экономического роста,
– темп экономического роста, 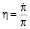 – темп прироста темпа инфляции. В модели величины n и g фиксированы.
– темп прироста темпа инфляции. В модели величины n и g фиксированы.
Тогда с учётом (7) и (10) запишем целевую функцию задачи максимизации реального сеньоража:
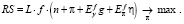 (11)
(11)
Для решения задачи (11) найдем производную функциональной зависимости реального сеньоража от темпа инфляции и приравняем ее к нулю:
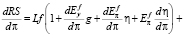
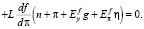 (12)
(12)
Если экономический рост отсутствует и численность экономически активного населения не изменяется (g = n = 0), то справедливо равенство
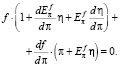 (13)
(13)
Так как выражение (13) описывает реакцию RS на близкое к нулю приращение темпа инфляции π, то η ≈ 0. И тогда получим приближенное равенство
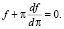 (14)
(14)
Из (14) следует, что, если величина π доставляет максимум функции реального сеньоража, то выполняется условие
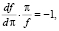 (15)
(15)
согласно которому при оптимальном темпе инфляции в экономике эластичность функции спроса на реальные запасы денег по темпу инфляции равна единице.
Для положительных g и n при η ≈ 0 выражение (12) можно записать в виде
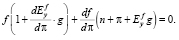 (16)
(16)
Если предположить, что эластичность реального спроса на деньги по доходу не зависит от темпа инфляции:
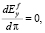 (17)
(17)
то условием для оптимального темпа π* инфляции будет следующее:
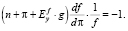 (18)
(18)
Очевидно, что целесообразность денежной эмиссии для извлечения реального дохода будет зависеть от соотношения фактического и оптимального темпов инфляции.
Протестируем модель оптимизации реального сеньоража по данным российской экономики. Источник данных – сайт Федеральной службы государственной статистики www.gks.ru.
Таблица 1
Исходные данные для эконометрического моделирования зависимости спроса на деньги от темпа инфляции и реального дохода с учетом состояния российской экономики dt
|
t |
Mt |
Yt |
πt |
dt |
|
1999 |
663,50 |
4823,23 |
36,53 |
0 |
|
2000 |
753,29 |
5218,32 |
20,18 |
1 |
|
2001 |
862,02 |
5323,56 |
18,58 |
1 |
|
2002 |
964,24 |
5372,29 |
15,06 |
1 |
|
2003 |
1278,50 |
5971,88 |
11,99 |
1 |
|
2004 |
1476,26 |
6294,92 |
11,73 |
1 |
|
2005 |
1706,33 |
6806,83 |
10,92 |
1 |
|
2006 |
2093,21 |
7065,51 |
9,00 |
1 |
|
2007 |
2805,31 |
7933,78 |
11,87 |
0 |
|
2008 |
2553,16 |
8208,17 |
13,28 |
0 |
|
2009 |
2726,98 |
7712,92 |
8,80 |
0 |
|
2010 |
3180,47 |
8063,71 |
8,78 |
0 |
|
2011 |
3293,30 |
9056,95 |
6,10 |
1 |
|
2012 |
3457,79 |
8695,62 |
6,57 |
0 |
|
2013 |
3810,50 |
8809,92 |
6,47 |
0 |
|
2014 |
3700,40 |
9723,01 |
11,35 |
0 |
|
2015 |
3715,31 |
9461,27 |
12,91 |
0 |
|
2016 |
4005,58 |
9456,72 |
5,39 |
0 |
|
2017 |
4184,37 |
9607,18 |
2,51 |
1 |
|
2018 |
4245,41 |
9823,56 |
4,26 |
0 |
В качестве исходной спецификации функции спроса на реальные запасы денежных средств рассмотрим уравнение
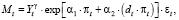 (19)
(19)
где Mt – денежная масса (агрегат M2) в постоянных ценах (1999 г.), млрд руб.; Yt – валовой внутренний продукт (ВВП) в постоянных ценах (1999 г.), млрд руб.; πt – темп инфляции, %, dt – фиктивная переменная, отражающая факт усиления кризисной ситуации в России под влиянием внешних и внутренних факторов; πt – случайное возмущение.
Фиктивная переменная dt принимает значение 0 в случае усиления кризисной ситуации в России или значение 1 в случае ее ослабления на протяжении периода с 1999 по 2018 г. В частности, dt = 0 для 2014–2015 гг. (валютный кризис, резкое ослабление российского рубля); для 2007–2013 гг. (мировой финансово-экономический кризис).
С целью линеаризации прологарифмируем уравнение (19):
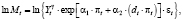 (20)
(20)
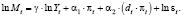 (21)
(21)
Оцененная модель имеет вид
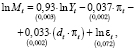 (22)
(22)
Для относительно стабильных лет для экономики России, dt = 1:
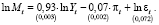 (23)
(23)
Для периодов усиления кризисных явлений, dt = 0:
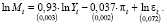 (24)
(24)
В моделях (23) и (24) в скобках под оценками параметров указаны стандартные ошибки, подтверждающие значимость полученных оценок.
Для рассматриваемого периода (1999–2018 гг.) средний темп экономического роста составлял g ≈ 0,039, т.е. имели место 4 % прироста реального ВВП в год. Средний темп прироста экономически активного населения за данный период n ≈ 0,003. Для оценки оптимального темпа инфляции воспользуемся формулой (18):
(n + π + γ∙g)∙α = –1.(25)
Для относительно стабильных лет для экономики России:
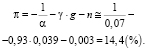 (26)
(26)
Для кризисных периодов в экономике:
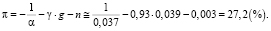 (27)
(27)
Таким образом, в соответствии с моделью Фридмана возможности для извлечения реального сеньоража в относительно более кризисные годы в России были выше в сравнении с относительно стабильными периодами. Снижение возможностей извлечения из денежной эмиссии реального сеньоража связано с повышением абсолютной величины коэффициента α, характеризующего эластичность спроса на деньги по темпу инфляции:
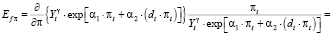
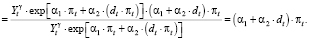 (28)
(28)
Эластичность спроса на деньги прямо пропорциональна темпу инфляции с коэффициентом пропорциональности α. Другими словами, относительная реакция спроса на деньги со стороны экономических агентов на прирост темпа инфляции на 1 % объясняется линейной функцией с угловым коэффициентом α. Чем выше α, тем более выраженной является реакция спроса на деньги при изменении темпа инфляции на 1 %. Для стабильных периодов развития российской экономики дополнительный прирост темпа инфляции πt на 1 % приводит к относительно более высокому по абсолютной величине снижению спроса на деньги (α = 0,07). Для периода усиления кризисных явлений реакция спроса на деньги на рост инфляции менее выраженная (α = 0,037).
Для относительно стабильных лет для экономики России, dt = 1:
α = α1 + α2. (29)
Для периодов усиления кризисных явлений, dt = 0:
α = α1. (30)
Основываясь на формулах (26) и (27), с учетом фактических темпов экономического роста gt получены оценки критических уровней темпа инфляции для каждого года в период с 1999 по 2018 г. (табл. 2).</p
Таблица 2
Сопоставление фактических и критических темпов инфляции с точки зрения извлечения максимального сеньоража от денежной эмиссии
|
t |
πt |
|
t |
πt |
|
|
1999 |
36,53 |
27,2 |
2009 |
8,80 |
27,2 |
|
2000 |
20,18 |
14,4 |
2010 |
8,78 |
27,2 |
|
2001 |
18,58 |
14,4 |
2011 |
6,10 |
14,4 |
|
2002 |
15,06 |
14,4 |
2012 |
6,57 |
27,2 |
|
2003 |
11,99 |
14,4 |
2013 |
6,47 |
27,2 |
|
2004 |
11,73 |
14,4 |
2014 |
11,35 |
27,2 |
|
2005 |
10,92 |
14,4 |
2015 |
12,91 |
27,2 |
|
2006 |
9,00 |
14,4 |
2016 |
5,39 |
27,2 |
|
2007 |
11,87 |
27,2 |
2017 |
2,51 |
14,4 |
|
2008 |
13,28 |
27,2 |
2018 |
4,26 |
27,2 |
Коэффициент детерминации для оцененной модели составляет величину 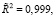 что подтверждает ее высокую объясняющую способность (рис. 5).
что подтверждает ее высокую объясняющую способность (рис. 5).
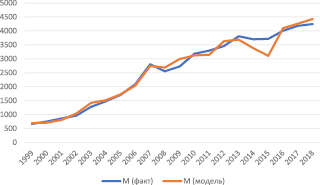
Рис. 5. Рост денежной массы (агрегат M2) в России
Модель Бруно – Фишера
В модели используется функция спроса на деньги вида
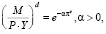 (31)
(31)
где 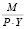 отражает удельный спрос на реальные запасы денежных средств.
отражает удельный спрос на реальные запасы денежных средств.
Модель предполагает возможность финансирования дефицита государственного бюджета за счёт денежной эмиссии. Доля бюджетного дефицита, покрываемого денежной эмиссией:
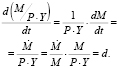 (32)
(32)
Темп экономического роста:
 (33)
(33)
Инфляционные ожидания адаптивны:
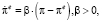 (34)
(34)
где параметр β – скорость пересмотра инфляционных ожиданий.
Условие равновесия рынка денег имеет вид
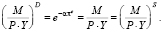 (35)
(35)
Прологарифмируем (35) и продифференцируем по времени t:
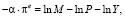 (36)
(36)
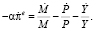 (37)
(37)
С учётом принятых выше обозначений перепишем (37) в виде
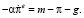 (38)
(38)
В силу (32) и (35) справедливо равенство
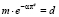 (39)
(39)
или
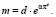 (40)
(40)
Далее, принимая во внимание (34) и (40), трансформируем уравнение (38) к виду
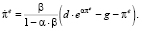 (41)
(41)
В состоянии равновесия экономики для (41) будет справедливо равенство
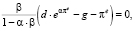 (42)
(42)
или
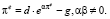 (43)
(43)
Проанализируем уравнение (43) с помощью его графической интерпретации (рис. 6).
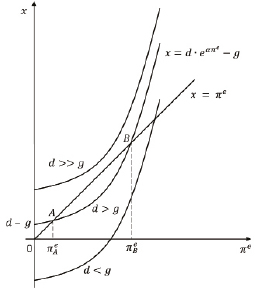
Рис. 6. Равновесие в модели Бруно – Фишера
Для этого введём вспомогательную переменную x. Запишем (43) в виде двух уравнений
x = πe, (44)
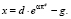 (45)
(45)
Возможные варианты решения уравнения (43) зависят от соотношения параметров d, g. Если d >> g, то графики уравнений (44) и (45) могут не иметь общих точек пересечения. Это значит, что, если доля бюджетного дефицита значительно превышает темп экономического роста, в экономике невозможно достижение равновесного состояния. Если, напротив, d < g, тогда уравнение (43) будет иметь единственное решение. Если d > g, достижимы два равновесных состояния в точках A и B. Точка A характеризуется относительно низким ожидаемым темпом инфляции. В точке B равновесие достигается при высоких инфляционных ожиданиях.
С помощью уравнения (41) можно показать, что при условии α∙β < 1 устойчивое равновесие достигается в точке A. При условии α∙β > 1 устойчивым является равновесие в точке B.
Пусть α∙β < 1. Тогда при инфляционных ожиданиях 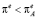 производная
производная 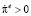 . Это значит, что инфляционные ожидания будут расти, пока экономика не придёт в состояние A. Если
. Это значит, что инфляционные ожидания будут расти, пока экономика не придёт в состояние A. Если 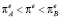 , тогда инфляционные ожидания будут снижаться до тех пор, пока не будет достигнута точка A. В случае выполнения неравенства
, тогда инфляционные ожидания будут снижаться до тех пор, пока не будет достигнута точка A. В случае выполнения неравенства 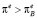 инфляционные ожидания будут расти неограниченно. Таким образом, устойчивое равновесное состояние экономики достигается в точке A.
инфляционные ожидания будут расти неограниченно. Таким образом, устойчивое равновесное состояние экономики достигается в точке A.
Пусть α∙β > 1. Тогда при инфляционных ожиданиях 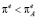 производная
производная 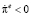 . Это значит, что в рамках модели Бруно – Фишера инфляционные ожидания будут неограниченно снижаться. Если
. Это значит, что в рамках модели Бруно – Фишера инфляционные ожидания будут неограниченно снижаться. Если 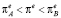 , производная
, производная 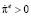 . Это значит, что ожидаемый темп инфляции будет расти до тех пор, пока экономика не достигнет равновесного состояния B. Если
. Это значит, что ожидаемый темп инфляции будет расти до тех пор, пока экономика не достигнет равновесного состояния B. Если 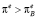 , то
, то 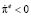 , и инфляционные ожидания будут падать до уровня
, и инфляционные ожидания будут падать до уровня 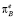 . Таким образом, устойчивое равновесие экономики достигается в точке B.
. Таким образом, устойчивое равновесие экономики достигается в точке B.
Оценка реакций российских экономических агентов на рост инфляции
Модель адаптации инфляционных ожиданий имеет вид
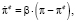 (46)
(46)
0 < β < 1.
Для дискретных переменных модель может быть записана в виде
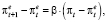 (47)
(47)
0 < β < 1.
В модели (47) предполагается, что приращение инфляционных ожиданий пропорционально ошибке ожиданий 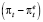 с коэффициентом пропорциональности β. Данный коэффициент характеризует скорость пересмотра инфляционных ожиданий и является показателем «нервозности» экономических агентов. Чем ближе β к единице, тем большее влияние оказывает фактический текущий темп инфляции на ожидаемый темп инфляции в предстоящем временном периоде.
с коэффициентом пропорциональности β. Данный коэффициент характеризует скорость пересмотра инфляционных ожиданий и является показателем «нервозности» экономических агентов. Чем ближе β к единице, тем большее влияние оказывает фактический текущий темп инфляции на ожидаемый темп инфляции в предстоящем временном периоде.
Переменная будущих инфляционных ожиданий 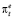 не наблюдаема. Поэтому для оценивания параметра β требуются специальные эконометрические построения.
не наблюдаема. Поэтому для оценивания параметра β требуются специальные эконометрические построения.
Рассмотрим спецификацию модели общего вида влияния ожидаемого (фактически не наблюдаемого) значения переменной Xt на фактически наблюдаемую переменную Yt:
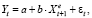 (48)
(48)
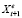 – ожидаемое значение регрессора в период t + 1. Так как значение переменной является ожидаемой оценкой, его заменяют наблюдаемой переменной, например, текущего или предшествующих периодов. Модели адаптивных ожиданий используются в ситуациях, когда экономические показатели чувствительны к ожиданиям относительно будущего.
– ожидаемое значение регрессора в период t + 1. Так как значение переменной является ожидаемой оценкой, его заменяют наблюдаемой переменной, например, текущего или предшествующих периодов. Модели адаптивных ожиданий используются в ситуациях, когда экономические показатели чувствительны к ожиданиям относительно будущего.
В модели (48) адаптивных ожиданий используется замена:
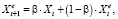 (49)
(49)
где 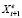 определяется как среднее взвешенное между текущим значением переменной Xt и её ожидаемым значением в предыдущий период
определяется как среднее взвешенное между текущим значением переменной Xt и её ожидаемым значением в предыдущий период 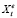 .
.
Данное выражение следует из модели адаптации ожиданий:
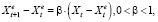 (50)
(50)
согласно которому приращение ожиданий пропорционально ошибке ожиданий.
В итоге исходная спецификация (48) принимает вид
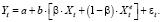 (51)
(51)
Для замены переменной 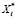 фактически наблюдаемой переменной проведем преобразование Койка. Запишем данное уравнение для момента t – 1 и умножим на множитель (1 – β):
фактически наблюдаемой переменной проведем преобразование Койка. Запишем данное уравнение для момента t – 1 и умножим на множитель (1 – β):
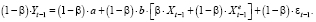 (52)
(52)
Разность двух уравнений (51) и (52):
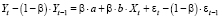 (53)
(53)
или
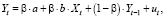 (54)
(54)
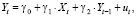 (55)
(55)
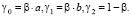 (56)
(56)
Инфляционные ожидания учитываются при реализации экономической, в частности денежно-кредитной, политики. Рассмотрим модель влияния ожидаемого темпа инфляции на уровень предложения денег в экономике.
Спецификация модели имеет вид
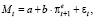 (57)
(57)
где Mt – денежная масса (агрегат М2) в постоянных ценах (1999 г.). После преобразования по описанной выше схеме получим уравнение
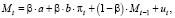 (58)
(58)
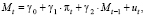 (59)
(59)
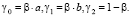 (60)
(60)
Для оценивания параметров модели использовались данные, представленные в табл. 1. Оцененная модель имеет вид
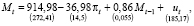 (61)
(61)
Все полученные оценки параметров статистически значимы. Объясняющая способность модели в соответствии с коэффициентом детерминации R2 составляет 98 %.
Согласно оцененной модели (61) коэффициент адаптации инфляционных ожиданий составляет величину 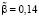 , т.е. имеет место следующее правило пересмотра инфляционных ожиданий:
, т.е. имеет место следующее правило пересмотра инфляционных ожиданий:
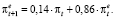 (62)
(62)
Из данного правила следует, что инфляционные ожидания 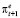 на 14 % определяются текущим фактическим темпом инфляции πt и на 86 % инфляционными ожиданиями текущего периода
на 14 % определяются текущим фактическим темпом инфляции πt и на 86 % инфляционными ожиданиями текущего периода 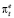 .
.
Модель, объясняющая уровень предложения денег Mt в экономике ожидаемой инфляцией 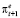 , имеет вид
, имеет вид
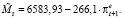 (63)
(63)
Согласно модели (63) увеличение в обществе инфляционных ожиданий на 1 % сопряжено с уменьшением предложения денег в российской экономике в среднем на 266,1 млрд руб.
Модель влияния ожидаемого темпа инфляции на инвестиционный спрос
Инфляционные ожидания играют значительную роль при принятии фирмами решений относительно инвестирования. Оценим параметры модели влияния ожидаемого темпа инфляции на инвестиционные расходы:
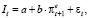 (64)
(64)
где It – инвестиции в основной капитал в постоянных ценах (1999 г.).
После перехода к фактически наблюдаемым переменным получим уравнение
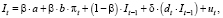 (65)
(65)
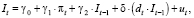 (66)
(66)
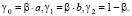 (67)
(67)
В уравнение (65), (66) добавлена фиктивная переменная наклона 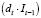 для отражения в модели влияния на значение параметра γ2 = 1 – β кризисных явлений в экономике, способных повлиять на правило пересмотра инфляционных ожиданий фирм.
для отражения в модели влияния на значение параметра γ2 = 1 – β кризисных явлений в экономике, способных повлиять на правило пересмотра инфляционных ожиданий фирм.
В данной модели фиктивная переменная dt принимает значение 1 в случае усиления кризисной ситуации в России или значение 0 в случае ее ослабления.
Оцененная модель имеет вид
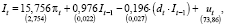 (68)
(68)
Полученные оценки параметров значимы. Объясняющая способность модели составляет 98 %.
В случае dt = 0 коэффициент адаптации инфляционных ожиданий бизнеса составляет величину 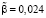 , т.е. имеет место следующее правило пересмотра инфляционных ожиданий:
, т.е. имеет место следующее правило пересмотра инфляционных ожиданий:
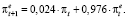 (69)
(69)
Из данного правила следует, что инфляционные ожидания 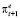 на 2,4 % определяются текущим фактическим темпом инфляции πt и на 97,6 % инфляционными ожиданиями текущего периода
на 2,4 % определяются текущим фактическим темпом инфляции πt и на 97,6 % инфляционными ожиданиями текущего периода 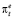 .
.
Соответственно, модель влияния инфляционных ожиданий на инвестиционный спрос имеет вид
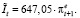 (70)
(70)
Для случая dt = 1 коэффициент равен 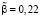 . В этом случае правило пересмотра инфляционных ожиданий имеет вид
. В этом случае правило пересмотра инфляционных ожиданий имеет вид
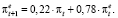 (71)
(71)
В случае усиления кризиса модель влияния инфляционных ожиданий на инвестиционный спрос имеет вид
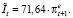 (72)
(72)
Согласно моделям (71) и (72) в России в период с 2001 по 2018 г. имели место следующие инфляционные ожидания, представленные в табл. 3.
Из модели Бруно – Фишера следует, что по величине произведения коэффициентов α и β можно судить о характере поведения экономических агентов. В соответствии с проведенными эконометрическими расчетами в рамках моделей эмиссионного финансирования Фридмана и Бруно – Фишера имеют место следующие оценки α∙β, представленные в табл. 4.
Таблица 3
Сопоставление фактических и ожидаемых темпов инфляции в российской экономике в период времени с 2001 по 2018 г.
|
Год |
πt |
|
Год |
πt |
|
|
2001 |
36,53 |
11,74 |
2010 |
13,28 |
22,36 |
|
2002 |
20,18 |
13,31 |
2011 |
8,80 |
2,72 |
|
2003 |
18,58 |
13,53 |
2012 |
8,78 |
2,68 |
|
2004 |
15,06 |
1,73 |
2013 |
6,10 |
2,79 |
|
2005 |
11,99 |
1,85 |
2014 |
6,57 |
21,27 |
|
2006 |
11,73 |
1,97 |
2015 |
6,47 |
17,77 |
|
2007 |
10,92 |
2,02 |
2016 |
11,35 |
17,52 |
|
2008 |
9,00 |
2,33 |
2017 |
12,91 |
2,06 |
|
2009 |
11,87 |
2,88 |
2018 |
5,39 |
2,05 |
Таблица 4
Количественные оценки «нервозности» российских экономических агентов
|
Состояние российской экономики |
α |
β |
α∙β |
|
Усиление кризисной ситуации |
0,037 |
0,22 |
0,0081 |
|
Ослабление кризисной ситуации |
0,07 |
0,024 |
0,0017 |
Таким образом, для российских экономических агентов, в частности инвесторов, в период с 1999 по 2018 г. характерна относительно низкая скорость пересмотра инфляционных ожиданий β и невысокая реакция спроса на деньги относительно текущего темпа инфляции при его увеличении на 1 %. При этом в периоды усиления кризисных явлений реакции на рост темпа инфляции существенно более выраженные.
Соответствующие инфляционным ожиданиям 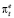 равновесные доли dt покрытия дефицита государственного бюджета за счет денежной эмиссии приведены в табл. 5.
равновесные доли dt покрытия дефицита государственного бюджета за счет денежной эмиссии приведены в табл. 5.
Таблица 5
Темпы экономического роста, инфляционные ожидания и соответствующие им равновесные доли финансирования дефицита государственного бюджета за счет дополнительной денежной эмиссии
|
Год |
gt |
|
dt |
Год |
gt |
|
dt |
|
2001 |
2,02 |
11,74 |
13,17 |
2010 |
4,55 |
22,36 |
26,49 |
|
2002 |
0,92 |
13,31 |
13,54 |
2011 |
12,32 |
2,72 |
15,01 |
|
2003 |
11,16 |
13,53 |
24,46 |
2012 |
-3,99 |
2,68 |
– |
|
2004 |
5,41 |
1,73 |
7,13 |
2013 |
1,31 |
2,79 |
4,06 |
|
2005 |
8,13 |
1,85 |
9,97 |
2014 |
10,36 |
21,27 |
29,24 |
|
2006 |
3,80 |
1,97 |
5,76 |
2015 |
-2,69 |
17,77 |
14,12 |
|
2007 |
12,29 |
2,02 |
14,29 |
2016 |
-0,05 |
17,52 |
17,26 |
|
2008 |
3,46 |
2,33 |
5,78 |
2017 |
1,59 |
2,06 |
3,64 |
|
2009 |
-6,03 |
2,88 |
– |
2018 |
2,25 |
2,05 |
4,29 |
Заключение
В ходе проведенного эконометрического исследования на основе теоретических моделей эмиссионного финансирования Фридмана и Бруно – Фишера были построены и оценены эконометрические модели с включением фиктивных переменных, отражающих общее состояние российской экономики с точки зрения усиления или ослабления дестабилизирующих факторов. Эконометрический анализ возможности эмиссионного финансирования дефицита государственного бюджета в рамках моделей Фридмана и Бруно – Фишера, представленный в данной статье, позволил сделать следующие выводы.
Для относительно стабильных лет развития российской экономики за период с 1999 по 2018 г. критический уровень темпа инфляции, при котором имелась возможность извлекать максимальный реальный сеньораж, составлял величину 14,4 %. Скорость пересмотра инвесторами инфляционных ожиданий β в эти годы составляла величину 0,024. Это означает, что инфляционные ожидания 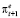 на 2,4 % определялись текущим фактическим темпом инфляции πt и на 97,6 % ожидаемым темпом инфляции на текущий период
на 2,4 % определялись текущим фактическим темпом инфляции πt и на 97,6 % ожидаемым темпом инфляции на текущий период 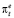 . Реакция функции спроса на деньги при увеличении темпа инфляции на 1 % прямо пропорциональна темпу инфляции с коэффициентом пропорциональности α = 0,07. Относительно низкая величина мультипликативного параметра α∙β = 0,0017 говорит о спокойных реакциях экономических агентов на рост инфляции.
. Реакция функции спроса на деньги при увеличении темпа инфляции на 1 % прямо пропорциональна темпу инфляции с коэффициентом пропорциональности α = 0,07. Относительно низкая величина мультипликативного параметра α∙β = 0,0017 говорит о спокойных реакциях экономических агентов на рост инфляции.
В годы усиления кризисных явлений в экономике России за период с 1999 по 2018 г. критический темп инфляции с точки зрения максимизации реального сеньоража был равен 27,2 %. Скорость пересмотра инфляционных ожиданий β для этих лет составляла величину 0,22. То есть инфляционные ожидания 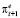 на 22 % определялись текущим фактическим темпом инфляции πt и на 78 % – ожидаемым темпом инфляции на текущий период
на 22 % определялись текущим фактическим темпом инфляции πt и на 78 % – ожидаемым темпом инфляции на текущий период 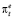 . Реакция спроса на деньги при увеличении темпа инфляции на 1 % прямо пропорциональна темпу инфляции с коэффициентом α = 0,37. Это означает, что в кризисные годы реакция экономических агентов на рост темпа инфляции менее «спокойная». В совокупности со скоростью пересмотра инфляционных ожиданий характеристика «нервозности» экономических агентов более высокая, α∙β = 0,0814.
. Реакция спроса на деньги при увеличении темпа инфляции на 1 % прямо пропорциональна темпу инфляции с коэффициентом α = 0,37. Это означает, что в кризисные годы реакция экономических агентов на рост темпа инфляции менее «спокойная». В совокупности со скоростью пересмотра инфляционных ожиданий характеристика «нервозности» экономических агентов более высокая, α∙β = 0,0814.