Принятие решений в экономических задачах зависит от лица, принимающего решение (ЛПР), и от объективной действительности, окружающей решаемую задачу. Математической моделью таких задач во многих случаях служит «Игра с природой», в которой рациональным игроком А является ЛПР, а природой П – объективная действительность. Природа случайным образом принимает одно из своих состояний, не имея в игре никакой цели. ЛПР, принимая решение в условиях неопределенности и будучи рациональным игроком, стремится из возможных стратегий выбрать наиболее эффективную. Для сравнения эффективностей или неэффективностей стратегий ЛПР должен выбрать удовлетворительный принцип оптимальности. Для этой цели существуют различные критерии оптимальности, например выигрыш-критерий Вальда [1; 2, с. 273–308], риск-критерий Сэвиджа [3; 2, с. 308–349] и др.
На наш взгляд, заслуживают внимания также критерии, позволяющие оценивать оптимальность стратегий с синтетической (совместной) точки зрения выигрышей и рисков. Такие критерии назовем синтетическими. В данной статье определен синтетический критерий Вальда – Сэвиджа [2, с. 652–655; 4, 5], который с успехом использовался для оптимизации, например, в таких областях, как инвестирование [6, 7], импортные операции [8], кредитование [9] и др. В связи с этим вопрос о существовании стратегий, оптимальных по критерию Вальда – Сэвиджа, является актуальным.
Для формулирования цели исследования дадим описание критерия Вальда – Сэвиджа, для чего предварительно напомним кратко необходимые определения.
Пусть в игре с природой: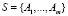 
, m ≥ 2 – множество стратегий 
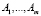игрока А; 
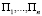, n ≥ 2 – состояния природы П; числа aij, 
, 
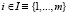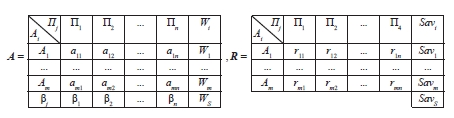
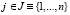– выигрыши игрока A в игровой ситуации (Ai, Пj); А – матрица выигрышей (платежная матрица) (1); 
, 
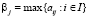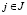– показатель благоприятности состояния Пj;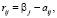 
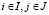, риск в игровой ситуации (Ai, Пj) [2, с. 18–25]; R – матрица рисков (1).
Критерий Вальда (W-критерий) [1; 2, с. 273–308] характеризуется следующими компонентами: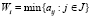 
– W-показатель эффективности стратегии Ai, 
; 
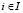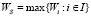– W-цена игры в стратегиях множества S; стратегия Ai W-оптимальна во множестве S, если 
; 
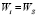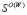– множество W-оптимальных стратегий. W-показатели стратегий и W-цена игры проставлены в дополнительном столбце матрицы А.
Критерий Сэвиджа (Sav-критерий) [3; 2, с. 308–349] описывается следующими составляющими: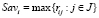 
– Sav-показатель неэффективности стратегии Ai, 
; 
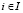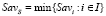– Sav-цена игры в стратегиях множества S; стратегия Ai Sav-оптимальна во множестве S, если 
; 
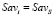– множество Sav-оптимальных стратегий. Sav-показатели стратегий и Sav-цена игры проставлены в дополнительном столбце матрицы рисков R.
В определении критерия Вальда – Сэвиджа важную роль играет выигрыш-показатель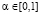 
. Он выражает степень предпочтения, отдаваемого игроком А выигрышам. Выбор 
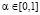игроком A является субъективным и связан с психологическими особенностями игрока А, определяющими его отношение к выигрышам и рискам. Величина 
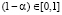является риск-показателем.
Критерий Вальда – Сэвиджа ((W-Sav)(α)-критерий) [2, с. 654] определяется следующим образом: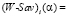 
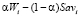– (W-Sav)(α)-показатель эффективности стратегии Ai, 
; 
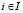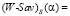
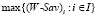– (W-Sav)(α)-цена игры в стратегиях множества S; стратегия Ai (W-Sav)(α)-оптимальна, если 
; 
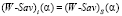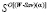-множество (W-Sav)(α)-оптимальных стратегий. Очевидно, что 
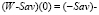критерий, а (W-Sav)(1) = W-критерий.
Стратегию Ai назовем синтезированной критерием Вальда – Сэвиджа с выигрыш-показателем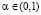 
(короче – (W-Sav)(α)-синтезированной), если она оптимальна по критерию Вальда – Сэвиджа с выигрыш-показателем α и неоптимальна ни по критерию Вальда, ни по критерию Сэвиджа.
Множество (W-Sav)(α)-синтезированных стратегий обозначим через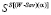 
.
Если ни при каком выигрыш-показателе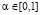 
не существует синтезированной стратегии, то будем говорить, что критерий Вальда – Сэвиджа не обладает свойством синтезирования.
Очевидно, что при выигрыш-показателях α = 0 и α = 1, (W-Sav)(α)-критерий свойством синтезирования не обладает.
По определению (W-Sav)(α)-критерия мы можем заключить, что он предназначен для синтезирования крайне высоких предпочтений, отдаваемых игроком А выигрышам (α = 1, W-критерий) и рискам (α = 0, Sav-критерий).
Применяя (W-Sav)(α)-критерий при определённом выигрыш-показателе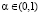 
, игрок А надеется в качестве оптимальной получить синтезированную стратегию, а не стратегию, оптимальную по исходным критериям Вальда или Сэвиджа. Проверить существование (W-Sav)(α)-синтезированных решений для каждого значения 
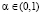принципиально невозможно, поскольку эти значения составляют бесконечное множество. В связи с этим возникает проблема синтезирования критерием Вальда – Сэвиджа, состоящая в отыскании условий, при которых критерий Вальда – Сэвиджа не обладает свойством синтезирования.
В [5] приведено аналитическое решение этой проблемы, т.е. найдены аналитические необходимые и достаточные условия на игру, при которых (W-Sav)(α)-критерий не обладает свойством синтезирования и, следовательно, применять его для отыскания синтезированных стратегий в этом случае не имеет смысла.
Цель настоящей статьи – анонсировать геометрическое решение указанной проблемы и проиллюстрировать приложение полученных результатов на анализе экономической задачи [5] оптимального выбора технологического способа производства.
Материалы и методы исследования
Показатель эффективности (W-Sav)i(α), который можно представить так: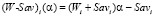 
, является линейной функцией аргумента 
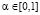. Стало быть, его графиком в системе координат αo(W-Sav)i(α) является отрезок (–Savi)Wi с левым концом 
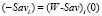и правым концом 
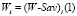. Следовательно, графиком цены игры (W-Sav)S(α) является верхняя огибающая m отрезков (–Savi)Wi, 
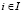, которая представляет собой ломаную, состоящую не более чем из m звеньев. На рис. 1 изображены отрезки (–Savi)Wi – графики (W-Sav)i(α), i = 1,...,7 и ломаная (–SavS)MWS c двумя звеньями – график цены игры (W-Sav)S(α).
Рассмотрим величины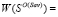 
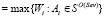и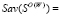 
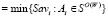, на основании которых определим следующие множества стратегий: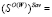 
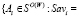
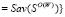-множество W-оптимальных стратегий Ai, показатель неэффективности которых Savi равен 
; 
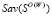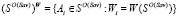-множество Sav-оптимальных стратегий Ai, показатель эффективности которых Wi равен 
.
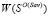Каждая стратегия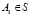 
порождает в системе координат 
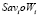точку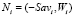 
с абсциссой (–Savi) и ординатой Wi. На рис. 2 изображены точки B, C, D, Ni, порождаемые стратегиями Ai, графики показателей, эффективности которых изображены на рис. 1.
Мы покажем, как по расположению точек Ni можно ответить на вопрос, обладает ли критерий Вальда – Сэвиджа свойством синтезирования или нет.
Построим в системе координат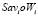 
(рис. 2) точки
, 
,
.
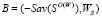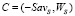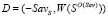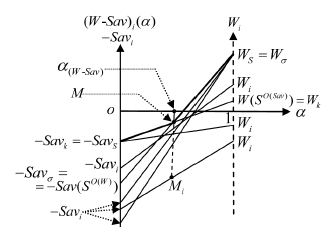
Рис. 1. Графики показателей эффективности стратегий и цены игры по критерию Вальда – Сэвиджа
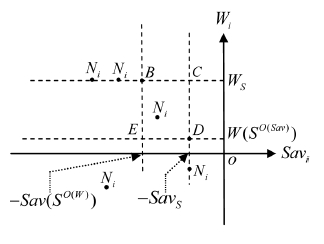
Рис. 2. Точки B, C, D, Ni , соответствующие отрезкам на рис. 1
Результаты исследования и их обсуждение
Теорема 1. Следующие утверждения эквивалентны: а) существует стратегия Ai, порождающая точку Ni = C; b) множество стратегий, оптимальных и по критерию Вальда, и по критерию Сэвиджа, не пусто; c) ломаная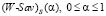 
, вырождается в отрезок (–SavS)WS; d) множество (W-Sav)(α)-оптимальных стратегий, совпадает с множеством стратегий, оптимальных и по критерию Вальда, и по критерию Сэвиджа:
, 
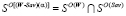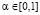. (2)
Теорема 2. Из каждого из утверждений теоремы 1 следует, что критерий Вальда – Сэвиджа не обладает свойством синтезирования.
Следствие 1. Если число стратегий m = 2, то критерий Вальда – Сэвиджа свойством синтезирования не обладает.
Пусть Q1 – внутренность треугольника BCD (рис. 3), Q2 – внутренность гипотенузы BD прямоугольного треугольника BCD (рис. 3) и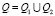 
.
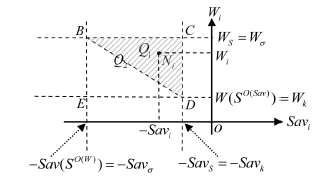
Рис. 3. Области Q1 и Q2
Теорема 3. Если не существует стратегии, порождающей точку C, то следующие утверждения эквивалентны: а) область Q не содержит точек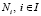 
; b) критерий Вальда – Сэвиджа не обладает свойством синтезирования; c) множество стратегий, оптимальных по критерию Вальда – Сэвиджа, имеет следующую структуру 
= 
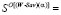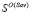, при α = 0; =
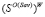, при 
; =
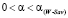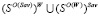, при 
; =
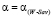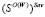, при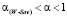 
; =
, 
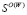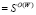, при α = 1, где
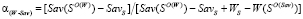. (3)
Задача [5]. Предприятие должно произвести X единиц продукции одним из четырех технологических способов. Спрос на количество этой продукции носит случайный характер и, как показывает маркетинговый анализ за прошлые периоды, может принимать значения 25, 35, 45 и 50 единиц. Производственные затраты TCi на изготовление X единиц продукции i-м (i = 1, 2, 3, 4) технологическим способом выражаются формулой
, 
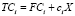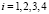, (4)
где FC1 = 145, FC2 = 70, FC3 = 180, FC4 = 110 условных денежных единиц (уе) – постоянные затраты и c1 = 3, c2 = 5, c3 = 2, c4 = 4 уе – удельные затраты на производство единицы продукции. Перед предприятием стоит задача выбора одного из четырех технологических способов изготовления продукции, при котором производственные затраты будут минимальными.
Решение. Применим модель «Игра с природой», в которой игрок А – предприятие; стратегии Ai, i = 1, 2, 3, 4, – «выбрать для изготовления продукции i-й технологический способ»; природа П – спрос на изготавливаемую продукцию; состояния природы – П1 = 25, П2 = 35, П3 = 45, П5 = 50 единиц спроса; выигрыши aij, i, j = 1, 2, 3, 4 – производственные затраты, вычисляемые по формуле (4):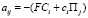 
, i, j = 1, 2, 3, 4.
Из подсчитанных выигрышей aij, i, j = 1, 2, 3, 4, формируем платежную матрицу А, находим показатели благоприятности состояний природы βj, j = 1, 2, 3, 4, вычисляем риски rij, i, j = 1, 2, 3, 4, и формируем матрицу рисков R. В качестве принципа оптимальности стратегий выберем критерий Вальда – Сэвиджа.
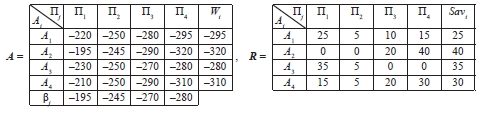
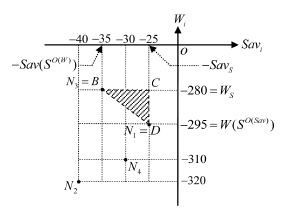
Рис. 4. Точки Ni, i = 1, 2, 3, 4
В матрицах А и R находим соответственно W-показатели Wi и Sav-показатели Savi, i = 1, 2, 3, 4. В системе координат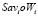 
, откладывая Sav-показатели со знаком "–" на горизонтальной оси oSavi, а W-показатели – на вертикальной оси oWi, строим точки 
, 
, 
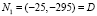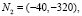
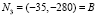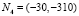(рис. 4). Из столбцов «Wi» и «Savi» матриц А и R очевидно, что WS = –280, 
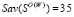, SavS = 25, 
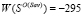. Среди построенных точек Ni, i = 1, 2, 3, 4, нет точки 
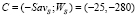и ни одна из построенных точек не попадает в область 
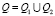(рис. 4). Поэтому по теореме 3 критерий Вальда – Сэвиджа не обладает свойством синтезирования, т.е. в данной игре нет синтезированных стратегий. По формуле (3) получаем 
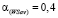. Из столбцов «Wi» и «Savi» матриц А и R очевидно, что, 
, 
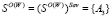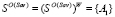. Тогда по утверждению c) теоремы 3 оптимальные несинтезированные стратегии образуют множество 
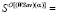{A1}, при 
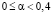; ={A1, A3}, при α = 0,4; ={A3}, при 
.
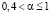Условно-геометрическая интерпретация данной задачи представлена на рис. 5.
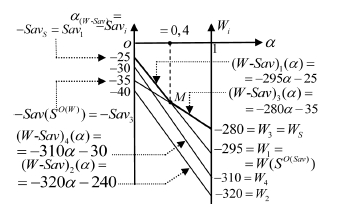
Рис. 5. Символическое расположение отрезков (–Savi)Wi, соответствующих точкам Ni на рис. 4
Заключение
В статье получены геометрические, легко проверяемые необходимые и достаточные условия, при которых критерий Вальда – Сэвиджа не обладает свойством синтезирования и, следовательно, при этих условиях применять его не имеет смысла. Анонсированные результаты являются новыми и имеют теоретическо-научное значение, поскольку привносят некий вклад в развитие теории игр с природой. Они имеют и практическую значимость, являясь новым методом в анализе задач по принятию финансово-экономических решений в условиях неопределенности.