В последние годы в научной литературе нередко встречаются статьи, посвященные исследованиям экономических систем в рамках различных физических моделей [1–3]. В работах [4, 5] авторы исследуют неравновесные экономические процессы, а также закон спроса и предложения на основе физических законов. В работе [6] проведено исследование зависимости национального дохода от времени с применением методов физических исследований. Поставленная задача решается в рамках модели гармонического осциллятора. При этом были рассмотрены свободные колебания осциллятора с затуханием. Целью настоящей работы является выяснение особенностей динамики изменения национального дохода в зависимости от времени в модели осциллятора с внешним периодическим воздействием. Математически задача сводится к решению обыкновенного неоднородного дифференциального уравнения с постоянными действительными коэффициентами.
Постановка задачи, метод решения и результаты исследования
Предположим, что национальный доход Y(t) удовлетворяет следующему обыкновенному дифференциальному уравнению гармонического осциллятора без учета затухания (коэффициент затухания η = 0), но с внешним периодическим воздействием:
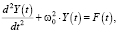(1)
где член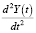 
есть темп изменения национального дохода (в физике – ускорение движения), член 
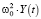соответствует рыночной силе (в физике – сила, возвращающая систему к точке равновесия), ω0 – частота собственных колебаний осциллятора (η = 0), 
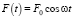есть периодически меняющиеся внешние инвестиции (в физике – внешняя действующая сила), ω и F0 = const – частота и амплитуда колебаний внешних инвестиций.
Заметим, что в работе [6] показано, что дифференциальное уравнение (1) для функции Y(t), аналогичное дифференциальному уравнению гармонического осциллятора, получается из динамической модели Кейнса, в основе которой лежит основной закон экономического баланса.
Как известно [7], общее решение линейного неоднородного дифференциального уравнения (1) имеет вид:
Y(t) = Yо.о.(t) + Yч.н.(t), (2)
где Yо.о.(t) есть общее решение соответствующего однородного уравнения, а Yч.н.(t) есть одно частное решение неоднородного уравнения. Решая соответствующее однородное уравнение методом Эйлера, для Yо.о.(t), получим:
Yо.о.(t) =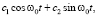 
(3)
где c1 и c2 – произвольные постоянные. Для нахождения частного решения Yч.н.(t) воспользуемся методом вариации произвольных постоянных. А именно, Yч.н.(t) ищем в виде:
Yч.н.(t) =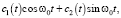 
(4)
где c1(t) и c2(t) пока не известные функции. Подставляя (4) в (1) для определения c1(t) и c2(t), получим систему уравнений:
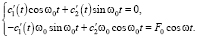(5)
Решение этой системы имеет вид:
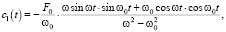(6)
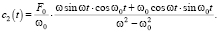(7)
Если теперь полученные выражения (6) и (7) для c1(t) и c2(t) подставить в (4) и провести несложные преобразования, то для Yч.н.(t) получим следующее выражение:
Yч.н.(t) =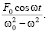
(8)
Тогда из (2) с учетом (3) и (8) имеем:
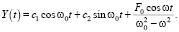(9)
Постоянные c1 и c2 в (9) определяются из начальных условий Коши:
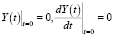(10)
и имеют вид:
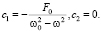(11)
Если теперь (11) подставить в (9), то после несложных преобразований для Y(t) получим выражение:
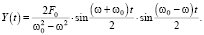(12)
Из (12) следует, что национальный доход как функция от времени в случае периодического изменения внешних инвестиций носит колебательный характер. Как известно [8], при выполнении условия совпадения частоты колебаний внешних инвестиций с частотой собственных колебаний системы происходит резонанс между двумя колебаниями. Для нахождения выражения национального дохода в случае резонанса перейдем к пределу в (12) при ω → ω0. Имеем:
Yрез.(t) =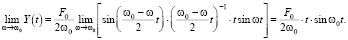 
(13)
Выражение (13) показывает, что явление резонанса приводит к усилению колебаний. Колебательный характер национального дохода сохраняется, но с увеличением t амплитуда колебаний возрастает (рис. 1).
Теперь перейдем к рассмотрению случая, когда не пренебрегаем затуханием собственных колебаний осциллятора (η ≠ 0), т.е. когда национальный доход удовлетворяет следующему неоднородному дифференциальному уравнению:
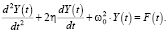(14)
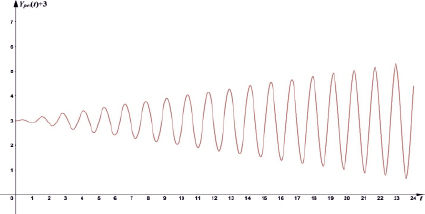
Рис. 1. Зависимость национального дохода от времени в случае резонанса при отсутствии затухания: η = 0; ω0 = 5; F0 = 1; 0 ≤ t ≤ 24
Отметим, что член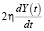 
в (14) показывает транзакционные издержки [8] (в физике – сила трения).
Как известно [6], при учете затухания (η ≠ 0) во всех случаях соотношения между η2 и 
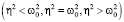со временем собственные колебания национального дохода затухают. Поэтому в рассматриваемом случае интерес представляет частное (вынужденное) решение уравнения (14). Для его нахождения будем пользоваться методом комплексных амплитуд, т.е. будем считать, что:
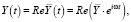
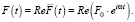(15)
Нетрудно показать, что через введенные комплексные величины уравнение (14) примет вид:
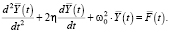(16)
Частное решение неоднородного дифференциального уравнения (16) ищем в виде:
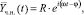(17)
где R и φ – пока не известные величины. Для их определения потребуем, чтобы (17) удовлетворяло уравнению (16). Подставляя (17) в (16) с учетом того, что:
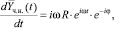
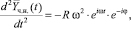
для величин R и φ получим следующие выражения:
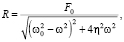
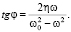(18)
Тогда из (17) с учетом (15) и (18), имеем:
Yч.н.(t) =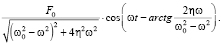 
(19)
Заметим, что амплитуда колебаний в (19) принимает максимальное значение при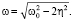 
Если коэффициент затухания η мал по сравнению с частотой ω0, то максимум амплитуды фактически достигается при частоте ω0 
т.е. когда имеет место резонанс. При этом из формулы (18) получим:
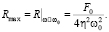(20)
Как следует из (20), в случае резонанса амплитуда колебаний национального дохода обратно пропорциональна коэффициенту затухания транзакционных издержек η. Чем больше η, тем меньше Rmax. Причем при η = 0 Rmax → ∞ (рис. 2).
Из (19) видно, что при резонансе все равно сохраняется колебательный характер национального дохода в зависимости от времени. На самом деле имеем:
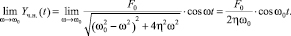(21)
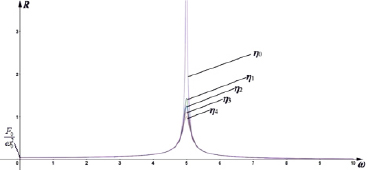
Рис. 2. Зависимость амплитуды колебаний национального дохода от частоты (резонансные кривые): F0 = 1, 0 ≤ ω ≤ 10, ω0 = 5, η1 = 0,07; η2 = 0,08; η3 = 0,09; η4 = 0,1; η0 = 0
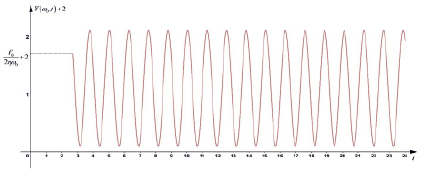
Рис. 3. Установление устойчивых колебаний национального дохода при резонансе: 1 – ω0 = 5,6; γ = 0,1; F0 = 1; 0 ≤ t ≤ 24
Через определенное время после начала действия внешних периодических сил с частотой ω (внешние периодические инвестиции) по мере приближения к резонансу (ω → ω0 устанавливаются устойчивые колебания национального дохода с постоянной амплитудой (рис. 3).
Полученные в работе результаты показывают, что динамика изменения национального дохода в зависимости от времени имеет особенности при наличии внешних периодических инвестиций. Если при отсутствии внешних инвестиций за счет транзакционных издержек собственные колебания национального дохода со временем затухают, то при наличии периодически меняющихся внешних инвестиций наступает явление резонанса, и это приводит к устойчивым колебаниям национального дохода с постоянной амплитудой.
Заключение
В работе исследована зависимость национального дохода от времени в классической модели гармонического осциллятора с внешним воздействием. При этом рассмотрены случаи, когда затухание не учитывается (η = 0), и случай с учетом затухания. Проведенный графический анализ полученных в работе аналитических результатов показывает, что наступление резонанса, когда частота периодических колебаний внешних инвестиций становится равной частоте собственных колебаний национального дохода, в случае отсутствия затухания приводит к возрастанию колебаний в зависимости от времени, а при учете затуханий приводит к устойчивому характеру колебаний национального дохода с постоянной амплитудой.