Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Модели векторной авторегрессии (VAR, vector autoregressive model), предложенные Кристофером Симсом в 1980 г. и предназначенные для описания нескольких динамических процессов на основе их общей истории, широко используются как альтернатива сложным структурным макроэкономическим моделям благодаря их гибкости, релевантности, сопоставимости по точности, простоте реализации и экономической интерпретации результатов [1–3]. Данный факт особенно важен для повышения мотивации студентов экономических направлений вузов к изучению многомерных моделей временных рядов в эконометрике и их применению при исследовании экономических процессов.

Модели векторной авторегрессии, с одной стороны, являются обобщением авторегрессионных моделей для многомерных временных рядов, с другой – частным случаем систем одновременных уравнений, сохраняя преемственность в методах оценивания, диагностики и исследования, изучаемых студентами бакалавриата в рамках базовой дисциплины «Эконометрика». При построении эконометрических моделей любых типов (моделей временных рядов, регрессионных моделей с одним уравнением, систем одновременных уравнений) одним из важнейших этапов является этап проверки выполнения их предпосылок – диагностика моделей. Большинство диагностических тестов (Diagnostic Tests) базируется на предпосылке нормальности распределения вектора возмущений. Нарушение этой предпосылки приводит к ошибочным выводам и интерпретации результатов оценивания [4, 5].

Для проверки нормальности распределения возмущений, по крайней мере в эконометрике, широкое применение получил тест Харке – Бера (Jarque-Bera), реализация которого выполнена практически во всех эконометрических пакетах [6–8]. Обобщенный вариант теста используется для проверки нормальности распределения вектора возмущений модели векторной авторегрессии. Для проверки остатков модели на наличие автокорреляции применяется обобщённая процедура тестов Бокса – Пирса (Box-Pierce Q-statistic) и Бокса – Льюинга (Ljung-Box Q-statistic). Для исследования гетероскедастичности в многомерных моделях временных рядов используются обобщенные тесты ARCH.

Поскольку в последние десятилетия в качестве инструментальной поддержки эконометрических методов оценки, диагностики и анализа моделей, в большинстве экономических вузов используется бесплатная альтернатива профессиональным специализированным пакетам – программная среда R [9], реализация многомерных тестов будет рассмотрена на языке R.

Обобщенный тест Харке – Бера на нормальность распределения ошибок модели VAR

Одним из достоинств моделей векторной авторегрессии является отсутствие необходимости априорных ограничений на параметры модели, гарантирующих идентификацию. Включенные в спецификацию переменные – эндогенные переменные модели, зависят от своих прошлых значений и прошлых значений других переменных.

Для упрощения анализа m-мерный VAR(p)-процесс представляют в виде mp-мерного VAR(1)-процесса (m – число переменных модели, p – максимальная величина лага) [10]. Такой подход реализован в функции VAR() пакета vars программной среды R и позволяет применять для оценки и прогнозирования векторной авторегрессии аппарат, разработанный для моделей авторегрессии одномерных временных рядов, а к диагностике моделей VAR(p) применять тесты, включающие обобщённые статистики одномерных аналогов.

Статистика одномерного (univariate) теста Харке – Бера (Jarque-Bera test) [6, 10] на нормальность распределения остатков эконометрической модели основана на сравнении центральных нормированных моментов третьего (коэффициент асимметрии, Skewness), 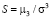, и четвертого (коэффициент эксцесса, Kurtosis) 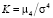порядков с соответствующими характеристиками нормального распределения, для которого, как известно, S = 0, K = 3, и имеет вид

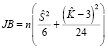. (1)

Оценки характеристик, включенных в формулу (1), вычисляются через остатки (e) регрессионной модели:

, ,

.

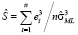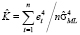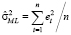Нулевая и альтернативная гипотезы теста Харке – Бера формулируются следующим образом: H0: S = 0, K = 3, H1: S ≠ 0, K ≠ 3.

Статистика (1) имеет распределение хи-квадрат с двумя степенями свободы, и, если вычисленное значение больше критического, нулевая гипотеза о нормальном распределении возмущений регрессионной модели не отклоняется. Тест Харке – Бера является асимптотическим тестом и применим к большим выборкам.

В обобщенной процедуре (multivariate) многомерного теста Харке – Бера, нормирование моментов выполняется при помощи матрицы факторизации P для оценки автоковариационной матрицы остатков модели VAR (p), представляющей собой нижнюю треугольную матрицу с положительными диагональными элементами (полученную при помощи разложения Холецкого), 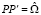. Разложение можно также записать через верхнюю треугольную матрицу 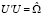, где 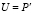. Статистика обобщенного теста вычисляется по формуле [10]:

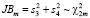, (2)

где

,

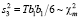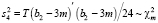, (3)

,

, .

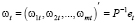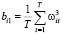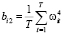Статистики (2), (3) реализованы в R при помощи функции normality.test() пакета {vars}: normality.test(x, multivariate.only = TRUE), с основными параметрами: x – объект класса "Varest", генерируемого VAR() или объект класса vec2var, генерируемого vec2var (); multivariate.only – логическая переменная, если TRUE (по умолчанию), вычисляется только статистика многомерного теста (2), если FALSE, вычисляются статистики для многомерного теста (2) и многомерных коэффициентов асимметрии и эксцесса (3). Объекты, созданные функциями с расширением test, поддерживают графическое представление эмпирического распределения остатков модели VAR(p) (и их квадратов), а также их автокорреляционной функции (ACF) и функции частных автокорреляций (PACF) [8].

Обобщенные тесты на автокорреляцию остатков

Для проверки адекватности моделей векторной авторегрессии, так же как и для моделей одномерных временных рядов, применяются тесты на отсутствие автокорреляции остатков, в частности обобщение тестов Бокса – Пирса (Box-Pierce Q-statistic) и Бокса – Льюинга (Ljung-Box Q-statistic), которые реализованы в эконометрических пакетах.

Для проверки нулевой гипотезы H0: ρ1 = ρ2 = ...= ρ_h = 0, против альтернативной 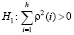, в тесте Бокса – Пирса используется статистика Q:

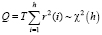, (4)

где ρi) – теоретические значения коэффициентов корреляции, r(i) – выборочные коэффициенты корреляции с числовыми характеристиками: 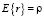, , 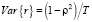h – порядок автокорреляции, для которого выполнена нулевая предпосылка. Если уровни временного ряда – белый шум, то коэффициенты автокорреляции 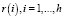асимптотически независимы и при большом объеме наблюдений 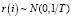. Вычисленное по формуле (4) значение статистики сравнивается с критическим, и если 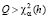, то нулевая гипотеза о белом шуме (отсутствии автокорреляции) отклоняется на уровне значимости α (правосторонняя критическая область). Обобщением статистики (4) для случая моделей VAR(p) является статистика теста Портманто (Portmanteau Test, (PT.asymptotic)):

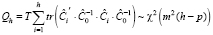, (5)

где

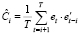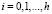, (6)

– оценка автоковариационной матрицы остатков модели VAR(p), p – порядок модели векторной авторегрессии, h – порядок автокорреляции, для которого выполнена нулевая предпосылка, m – число эндогенных переменных модели. Статистика (5) используется для проверки нулевой гипотезы:

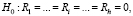(7)

где Ri – автокорреляционная матрица, оценка которой вычисляется по формуле

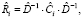(8)

где 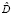– диагональная матрица с диагональными элементами, равными стандартным ошибкам возмущений VAR(p)-процесса

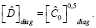
На малых выборках используют тест Бокса – Льюинга со статистикой

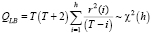, (9)

в которую каждое слагаемое входит со своим весом .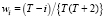

Обобщенный (многомерный) вариант статистики (9) для моделей VAR(p) с учетом (5) принимает вид (PT.adjusted):

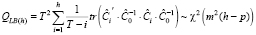. (10)

Для тестирования автокорреляции используется также обобщенный вариант теста Бреуша – Годфри. Тест является асимптотическим, то есть для достоверности выводов требуется большой объём выборки. В тесте рассматривается авторегрессия остатков на их лаговые значения и оцениваются две модели: исходная модель VAR(p) (усечённая, с ограничениями, restricted)

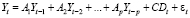, (11)

и вспомогательная, общая (неусеченная, без ограничений, unrestricted) модель

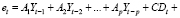
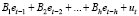, (12)

где et – остатки, полученные в результате МНК оценивания основной модели (11), et–j = 0 при t < j +1. Если нулевая гипотеза

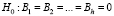
(против альтернативной 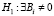для i = 1,2...,h) верна, то при большом значении объема выборки Т статистика теста определяется по формуле [8]:

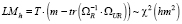, (13)

где Ω_R – автоковариационная матрица вектора остатков исходной (усечённой) модели VAR(p) (11), Ω_UR – автоковариационная матрица вектора остатков неусеченной модели (12), m – число эндогенных переменных модели, имеет хи-квадрат распределение с параметром hm2, и гипотеза не отклоняется при уровне значимости α, если выполняется неравенство

.

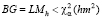Тесты на проверку наличия автокорреляции реализованы в программной среде R при помощи функции serial.test() пакета{vars}:

serial.test (x, lags.pt, lags.bg, type = c("PT.asymptotic", "PT. adjusted", "BG")),

с основными аргументами: x – объект, генерируемый функцией VAR(); lags.pt – величина лага, используемая в статистике теста Портманто (5), lags.bg – величина лага, используемая в статистике теста Бреуша – Годфри (13); type – тип теста: PT.asymptotic – (5); PT.adjusted – (10); BG – Breusch-Godfrey – (13). По умолчанию используется асимптотический тест Портманто.

Обобщенные тесты на гетероскедастичность остатков

Для исследования гетероскедастичности в многомерных моделях временных рядов используются тесты ARCH, основанные на оценивании вспомогательной модели вида [10]:

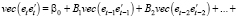
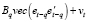, (14)

где vt – процесс белого шума, vec(•) – оператор формирования вектора из нижней треугольной матрицы с элементами на главной диагонали и вертикальным выстраиванием её столбцов. Для реализации оператора vec(•) в программной среде используется функция lower.tri(x,diag=TRUE), пакета {base}, с основными параметрами: x – матрица, diag – логическая переменная: TRUE – включать элементы на главной диагонали, FALSE – не включать элементы на главной диагонали. Если размерность матрицы x – (m×m), то сформированный вектор имеет размерность – m(m + 1)/2.

Таким образом, размерность параметров в модели (14):

β₀ – m(m + 1)/2, Bi – 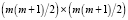, i = 1,...,q.

Нулевая и альтернативная гипотезы формулируются следующим образом:

, ,

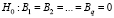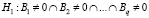и проверяются при помощи статистики

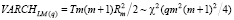, (15)

с коэффициентом детерминации:

,

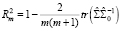где 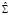– автоковариационная матрица вектора возмущений модели без ограничений на параметры, 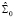– с ограничениями на параметры в рамках гипотезы H0. Статистика (15) реализована в программной среде R в виде функции arch.test() пакета vars, которая вычисляет одномерные и многомерные тесты ARCH-LM для моделей VAR (p). Основные параметры функции:

arch.test(x, lags.single = 16, lags.multi = 5, multivariate.only = TRUE),

где x – объект класса "Varest", генерируется VAR () или vec2var(); lags.single – целое число, указывающее величину лага для одномерной статистики ARCH; lags.multi – целое число, указывающее величину лага для многомерной статистики ARCH; multivariate.only – Если TRUE (по умолчанию), вычисляется только статистика многомерного теста.

В таблице приведены скрипт и фрагмент протокола результатов оценивания и диагностики модели векторной авторегрессии VAR(1), оцененной для двух эндогенных переменных: объём инвестиций и величина капитала, по годовым данным фирмы «General Electric» за 20 лет, встроенным в пакет "AER".

Результаты оценки и диагностики модели VAR(p)

Выводы

Как следует из протокола, остатки модели имеют нормальное распределение. Включение лаговых переменных в спецификацию Var(p) позволило преодолеть проблему автокорреляции, уточнить причинно-следственные связи и повысить качество модели.

С точки зрения образовательного процесса аппарат Var-моделей полностью соответствует принципу систематичности и последовательности обучения: новый учебный материал по построению и диагностике VAR (p) моделей базируется на знаниях ранее изученных эконометрических методов, расширяет и дополняет их.