Революционные изменения в развитии современной экономики во многом связаны с появлением новых (аддитивных, бережливых, роботизированных и т.д.) технологий, позволяющих значительно повысить эффективность производства. Однако отсутствие достаточного опыта использования технологических инноваций не позволяет предусмотреть (и в должной мере компенсировать) их возможные негативные экономические последствия. Так, например, недостаточно продуманное внедрение современных агротехнологий может привести к негативным структурным изменениям на рынке труда и, как следствие, к снижению устойчивости социально-экономического развития сельских территорий. При этом общие методологические положения федеральных ([1, 2]) и региональных ([3]) программ в сфере инноватики не могут быть просто перенесены на уровень предприятий (организаций), непосредственно внедряющих инновации, что делает практически значимой задачу поддержки принятия научно обоснованных организационно-экономических решений по выбору способов внедрения и использования инновационных производственных технологий.
Одним из эффективных подходов к решению этой задачи является использование инструментария имитационного моделирования [4], позволяющего в рамках вычислительного эксперимента рассмотреть различные сценарии и выбрать наиболее рациональный (оптимальный) из них. При этом (несмотря на развитие методологии имитационного моделирования [5, 6]) остается актуальной научная задача разработки специализированных инструментальных средств моделирования инновационных производственно-экономических процессов.
Цель исследования состоит в разработке инструментария количественной оценки степени адекватности рассматриваемой имитационной модели анализируемым инновационным производственно-экономическим процессам, что является одним из основных этапов моделирования.
Материалы и методы исследования
Методология имитационного моделирования предполагает выполнение этапов, формализованно представленное в нотации IDFF3 ([7]) на рисунке. Для обеспечения достоверности результатов важное значение имеет тестирование имитационной модели, содержание которого связано не только с выявлением ошибок программной реализации модели (верификация), но и с проверкой ее адекватности (валидация), предполагающей сравнение результатов модельных вычислительных экспериментов с известными данными, полученными на изучаемом объекте. Неудовлетворительные результаты проверки предполагают возврат и прохождение трех предыдущих этапов имитационного моделирования на более высоком методологическом уровне. Специфика инновационных процессов должна быть учтена при формировании перечня сравниваемых характеристик и оценочных показателей соответствия их вычисленных значений контрольным значениям, а также при построении способа вычисления значений этих показателей.
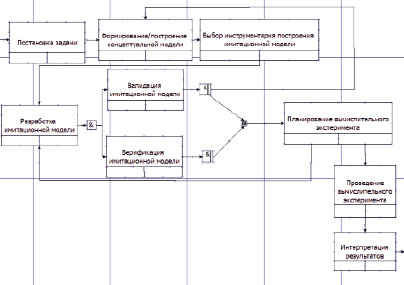
Контекстная диаграмма процесса имитационного моделирования в нотации IDFF3, разработанная с использованием редактора диаграмм Dian (проект GNU)
Результаты исследования и их обсуждение
Рассмотрим формальное представление дискретной имитационной модели инновационных производственно-экономических процессов Im в виде кортежа:
Im = < Char, Temp, Func>, (1)
где Char – совокупность характеристик исследуемого процесса;
Temp = {t1, t2,…, tn} – совокупность моментов времени, в которые рассматриваются значения характеристик процесса (моменты времени могут быть выбраны равномерно из некоторого интервала или связаны с определенными событиями);
Func – совокупность функциональных зависимостей между значениями характеристик процесса в рассматриваемые моменты времени.
В рамках методологии PESTI-анализа (в соответствии с [8, 9]) для исследования инновационных производственно-экономических процессов ограничимся рассмотрением только экономической (Economic, E), технологической (Technical, T) и инновационной (Inovatic, I) составляющих процесса, что позволяет выделить из множества характеристик Char подмножества характеристик CharE, CharT, CharI, соответствующих этим составляющим:
CharE, CharT, CharI ⊂ Char,
CharE ∪ CharT ∪ CharI = Char, (2)
CharE = {CharE1, CharE2,…, CharEs(E)},
CharT = {CharT1, CharT2,…, CharTs(T)},
CharI = {CharI1, CharI2,…, CharIs(I)}.
Рассмотрим характеристики процесса (2) в заданные моменты времени:
CharEr(ti), r = 1, 2, …, s(E), (3)
CharTr(ti), r = 1, 2, …, s(T),
CharIr(ti), r = 1, 2, …, s(I),
ti ∈ T.
Хотя представленный набор характеристик (3) полностью описывает инновационный производственно-экономический процесс, его непосредственное использование для решения задач оценки валидности имитационной модели представляется неоправданным в силу большого числа и разной степени значимости характеристик (3). В связи с этим предлагается наряду с характеристиками (3) использовать агрегированные по времени (взвешенные средние по времени) характеристики (2), используя формулы аддитивной свертки:
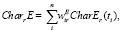
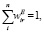
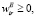(i = 1,2, …, n), r = 1, 2, …, s(E), (4)
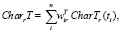
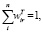
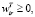
(i = 1,2, …, n), r = 1, 2, …, s(T)
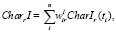
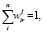
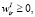
(i = 1,2, …, n), r = 1, 2, …, s(I)
ti ∈ T,
где весовые коэффициенты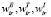 
отражают относительную важность значений характеристик CharEr, CharTr, CharIr в разные моменты времени из множества Temp. Весовые коэффициенты могут быть определены в результате обработки экспертных суждений (например, методом парных сравнений [10]), что, однако, требует отдельного исследования вопроса чувствительности решения к возможным изменениям мнений экспертов [11]. Следует отметить, что поскольку соответствующие исходные (3) и агрегированные по времени (2) характеристики инновационных производственно-экономических процессов имеют одинаковую размерность, то использование (4) не требует их предварительного приведения к безразмерному виду. В случае построения полной иерархии показателей ([12]), предполагающей последующее агрегирование характеристик CharEr, CharTr, CharIr по соответствующим подмножествам характеристик (CharE, CharT, CharI ) такая процедура была бы необходима.
Оценим показатели степени соответствия значений характеристик CharEr(ti)j, CharTr(ti)j, CharIr(ti)j, j = 1,2.,…,m, полученных в результате вычислительного эксперимента CompExpj (j = 1,2.,…,m) с использованием имитационной модели (1), имеющимся тестовым «контрольным» значениям TestCharEr(ti)j, TestCharTr(ti)j, TestCharIr(ti)j (здесь индекс j = 1,2.,…,m соответствует номеру вычислительного эксперимента).
Вербально-числовая шкала оценки результатов тестовых вычислительных экспериментов
|
№ п/п |
Вербальное значение показателя степени соответствия |
Числовое значение показателя степени соответствия |
|
1 |
«очень низкий» |
0 |
|
2 |
«низкий» |
0,25 |
|
3 |
«средний» |
0,5 |
|
4 |
«высокий» |
0,75 |
|
5 |
«очень высокий» |
1 |
Поскольку показатель соответствия Cong(CharEr(ti)j, TestCharEr(ti)j) (а также Cong(CharEr(ti)j, TestCharEr(ti)j), Cong(CharEr(ti)j, TestCharEr(ti)j)) должен отражать не только близость числовых значений (что обычно моделируется в виде абсолютной величины разности, относительной разности или отношения соответствующих значений), но и специфику предметной области (включая особенности экономической задачи, решаемой с использованием аппарата имитационного моделирования), то для его измерения предлагается использовать вербальные экспертные оценки в шкале с пятью уровнями градации: < «очень низкий», «низкий», «средний», «высокий», «очень высокий»>. Для перехода от вербальных значений к числовым значениям показателя соответствия воспользуемся методом семантического дифференциала ([13]), в результате чего получим модифицированную (смещенную и нормированную) шкалу Осгуда, представимую таблицей.
Безразмерный вид оценочных показателей Cong(CharEr(ti)j, TestCharEr(ti)j), Cong(CharEr(ti)j, TestCharEr(ti)j), Cong(CharEr(ti)j, TestCharEr(ti)j ) позволяет не только стоить соответствующие агрегированные по времени показатели соответствия (используя аналоги формул (4) при сохранении обозначений из (4)):
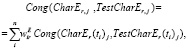(5)
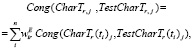
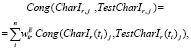
но и проводить агрегирование более высокого уровня.
Проведем агрегирование показателей Cong(CharE(ti), TestCharE(ti)j), Cong(CharE(ti)j, TestCharE(ti)j), Cong(CharE(ti)j, TestCharE(ti)j) (полученных при помощи формул (5)) по множествам CharE, CharT, CharI, получив общие показатели степени соответствия экономических, технологических и инновационных характеристик, полученных в результате вычислительного эксперимента CompExpj (j = 1,2.,…,m), контрольным значениям:
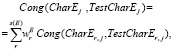(6)
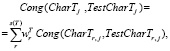
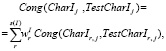
где весовые коэффициенты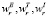 
отражают относительную важность характеристик CharEr, CharTr, CharIr в своих группах характеристик CharE, CharT, CharI. При этом выполняются обычные условия неотрицательности и нормировки входящих в (6) весовых коэффициентов:
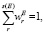
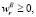r = 1, 2, …, s(E), (7)
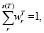
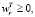r = 1, 2, …, s(T),
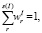
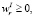r = 1, 2, …, s(I).
Поскольку формулы (6), (7) определяют качество моделирования применительно к экономической, технологической и инновационной составляющей исследуемого процесса в рамках одного тестового вычислительного эксперимента CompExpj, то естественно обобщить эти показатели для всего комплекса тестовых экспериментов CompExp = {CompExp1, CompExp2, …, CompExpm}:
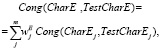(8)
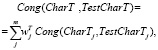
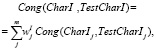
где весовые коэффициенты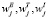 
отражают относительную значимость вычислительных экспериментов CompExpj (j = 1,2.,…,m) для определения экономических, технологических и инновационных характеристик моделируемого процесса в рамках дальнейших исследований (условия тестовых экспериментов могут в разной степени соответствовать условиям вычислительных экспериментов, выполнение которых предполагается в рамках имитационного моделирования исследуемых инновационных производственно-экономических процессов). Для весовых коэффициентов относительной значимости вычислительных экспериментов также должны выполняться условия неотрицательности и нормировки весовых коэффициентов:
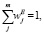
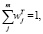
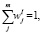
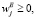
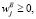
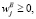(j = 1,2.,…,m). (9)
Иерархию показателей степени соответствия результатов тестовых вычислительных экспериментов CompExp контрольным значениям завершает общий показатель Cong(Char, CompExp), определяемый в виде аддитивной свертки
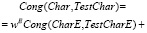(10)
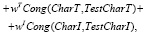
где весовые коэффициенты wE, wT, wI (wE, wT, wI ≥ 0, wE + wT + wI = 1 отражают относительную значимость экономических, технологических и инновационных составляющих моделируемых процессов в рамках исследования.
Заключение
Построенная иерархия оценочных показателей позволяет комплексно оценить рассматриваемую имитационную модель инновационных производственно-экономических процессов за счет учета экспертных суждений, отражающих:
– относительную важность несовпадения вычисленных и контрольных значений отдельных характеристик процессов в заданные моменты времени в рамках тестовых вычислительных экспериментов;
– относительную значимость отдельных характеристик в составе выделенной (экономической, технологической, инновационной) группы характеристик;
– относительную значимость отдельного тестового вычислительного эксперимента (как степень его соответствия планируемым экспериментам в рамках предстоящего имитационного исследования) в составе комплекса экспериментов;
– относительную значимость экономической, технологической и инновационной составляющих моделируемого процесса в рамках цели исследования.
Практическая значимость работы связана с возможностью использования числовых значений оценочных показателей степени соответствия (адекватности) имитационной модели инновационных производственно-экономических процессов для разработки и использования решающих правил валидации модели (переход к ее использованию или возврат на этап разработки концептуальной модели).
Планируемые дальнейшие исследования связаны с использованием построенных оценочных показателей при эволюционном структурно-параметрическом синтезе (в соответствии с методологией [14]) имитационных моделей инновационных производственно-экономических процессов.
Исследование выполнено при финансовой поддержке РФФИ и Правительства Белгородской области в рамках научного проекта № 18-47-310008.