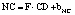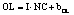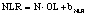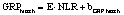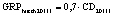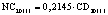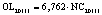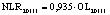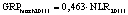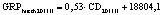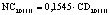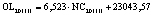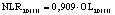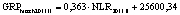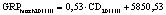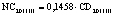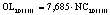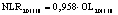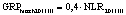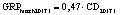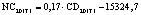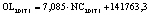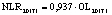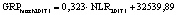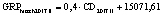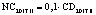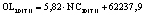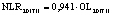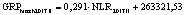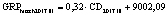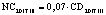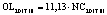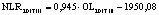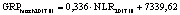Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Изучение и анализ факторов, определяющих экстенсивный и интенсивный рост инновационного сегмента экономической системы региона в условиях экономики знаний, несомненно, представляет научный интерес для развития экономической науки. Обратимся к исследованиям, связанным с данной проблемой. Исследование М.Ю. Мишиной посвящено анализу воздействия экстенсивных и интенсивных факторов на ВРП региона, автор проводит подобный анализ на примере Брянской области [1]. С.В. Арженовский и Р.В. Шеховцов, Т.А. Балина и З.В. Пономарева, [2, 3] в своих работах изучают социально-экономическое развитие субъектов РФ, обусловленное влиянием инновационных и экономических процессов под воздействием интенсивных факторов. Другие ученые [4–7] в качестве интенсивных факторов развития территорий определяют факторы опосредованного воздействия. По их мнению, данные факторы формируют условия, в которых происходит перераспределение финансовых ресурсов в рамках регионального кредитного механизма, направленное на стимулирование ВРП.

Однако перечисленные выше научные публикации не дают точного ответа на то, как дифференциация экономического развития субъектов РФ отражается на проявлении интенсивных и экстенсивных финансовых факторах, стимулирующих процесс формирования высокотехнологичного сегмента валового регионального продукта. В связи с недостаточной разработанностью данной научной тематики, развитие методических аспектов анализа прямых и опосредованных факторных связей, характеризующих процесс стимулирования высокотехнологичного сегмента ВРП за счет финансового капитала, в условиях неравномерного экономического регионального развития следует считать актуальным и перспективным направлением научных исследований.

Цель исследования: проверка с помощью парной линейной регрессионной модели гипотезы о существовании прямой и опосредованной факторной связи между объемом высокотехнологичного ВРП и величиной клиентских средств в банках для субъектов РФ, сгруппированных в экономические кластеры. Косвенным результатом проверки выступает установление факта применимости модели GRPhitech = f(CD) [8] и модели FINE [9] в качестве аналитического инструмента в отношении региональных кластеров при планировании стратегий развития субъектов РФ.

Теоретические аспекты и методы исследования

Теоретические аспекты, обосновывающие факторную связь между объемом высокотехнологичного валового регионального продукта за соответствующий год (GRPhitech) и величиной среднегодового регионального финансового капитала, привлекаемого и перераспределяемого системой коммерческих банков (CD), приводятся в исследовании «Методические аспекты анализа зависимости валового регионального продукта высокотехнологичных отраслей от финансовых факторов в условиях экономики знаний» [8]. Там же [8] на основе статистических методов была подтверждена гипотеза о наличии данной факторной связи и получено уравнение парной регрессии, иллюстрирующее зависимость факторов друг от друга: GRPhitech = MGRP hitech•CD + + cGRP hitech. По итогам проверки гипотезы авторами были сформированы модельные уравнения для каждого года по всей совокупности исследуемых регионов. Вычисленные в работе [8] уравнения экономико-математических моделей иллюстрируют, что экстенсивный рост высокотехнологичного сегмента ВРП может быть простимулирован за счет направления капитала, привлеченного системой коммерческих банков, в бизнес-процессы генерации добавленной стоимости. Факторы интенсивного роста суммарно характеризуются мультипликатором трансформации финансового капитала в высокотехнологичный ВРП(M GRP hitech) [8].

В статье «Декомпозиционный анализ зависимости объема валового регионального продукта высокотехнологичных отраслей от финансовых факторов в условиях экономики знаний» [9] была сформулирована модель FINE, которая описывает воздействие финансовых факторов на интенсивность процесса трансформации финансового капитала в высокотехнологичный сегмент ВРП. Теоретической основой модели FINE явилась предложенная авторами система, предполагающая цепную обусловленность, входящих в нее факторов и описывающая процесс трансформации финансового капитала в высокотехнологичный общественный продукт. Модель FINE была построена через механизм сопоставления уравнения регрессии ключевой факторной пары GRPhitech = f(CD) (средства клиентов>ВРП высокотехнологичных отраслей) и уравнений регрессии промежуточных факторных пар: «CD>NC» (средства клиентов>новые банковские кредиты); «NC>OL» (новые банковские кредиты>совокупная задолженность по кредитам); «OL>NLR» (совокупная задолженность по кредитам>чистая ссудная задолженность по кредитам); «NLR>GRP hitech» (чистая ссудная задолженность по кредитам>ВРП высокотехнологичных отраслей). Разработанная модель FINE может быть использована в качестве аналитического инструментария при планировании сценариев инновационного и финансового развития регионов в рамках интенсивного пути развития [9]. Однако модельные уравнения ключевой пары факторов и уравнений регрессии промежуточных пар факторов в работах [8, 9] были идентифицированы для всей совокупности исследуемых регионов без учета особенностей дифференциации регионального экономического развития. В связи с этим закономерно возникает вопрос о том, влияет ли уровень регионального экономического развития на процесс перераспределения капитала, запускаемый системой коммерческих банков? Иными словами, как проявляется сила выявленных факторных связей в регионах в зависимости от уровня регионального экономического развития.

Если дифференциация экономического развития субъектов РФ обуславливает ослабление зависимости указанных факторов для определенных региональных кластеров, то планировать управленческие воздействия на базе причинно-следственных связей, логика которых задается на основе модели FINE или модели GRPhitech = f(CD), в сценариях инновационного и финансового развития регионов нужно с осторожностью. Указанные причинно-следственные связи можно считать достоверными для модели GRPhitech = f(CD) при условии, что уравнение ключевой факторной пары для данной кластерной совокупности характеризуется достаточным качеством. Аналогично модель FINE целесообразно применять, если подтверждена ее достоверность для конкретной кластерной совокупности, то есть и уравнение ключевой факторной пары, и уравнения промежуточных факторных пар в отношении рассматриваемой кластерной совокупности характеризуются достаточным качеством. В противном случае строить умозаключения, опираясь на причинно-следственные связи, задаваемые моделью FINE и моделью GRPhitech = f(CD), нельзя.

Алгоритм проверки воздействия уровня регионального экономического развития на процесс перераспределения капитала, запускаемый системой коммерческих банков, будет нами реализован следующим образом.

На первом этапе выделяется количественный признак, позволяющий провести группировку регионов по уровню экономического развития. В соответствии с признаком, характеризующим региональное экономическое развитие, формируются региональные кластеры. По итогам группировки в рамках второго этапа формируются числовые ряды для каждого кластера по следующим переменным:

CD – среднегодовой объем средств клиентов, привлеченных коммерческими банками на территории субъекта РФ [9, с. 15];

NC – среднегодовая величина кредитов, вновь выданных кредитными организациями физическим и юридическим лицам (экономическим субъектам), осуществляющим свою деятельность на территории региона РФ [9, с. 16];

OL – среднегодовая величина совокупной ссудной задолженности кредитных организаций в рамках кредитования физических и юридических лиц (экономических субъектов), осуществляющих свою деятельность на территории региона РФ[9, с. 16];

NLR – среднегодовая величина чистой ссудной задолженности кредитных организаций в рамках кредитования физических и юридических лиц (экономических субъектов), осуществляющих свою деятельность на территории региона РФ [9, с. 16];

GRPhitech – объем производства высокотехнологичных отраслей, входящий в ВРП субъекта РФ [9, с. 16].

Третий этап проверки связан с тем, что на основе упомянутых переменных строятся числовые ряды по факторным парам. С помощью регрессионного и корреляционного анализа определяется теснота связи между признаками факторных пар и идентифицируются уравнения линейной парной регрессии, объясняющие связь между факторами. Проводится анализ качества полученных уравнений для каждого кластера. Формулируется вывод о применимости модели GRPhitech = f(CD). Если уравнение ключевой факторной пары кластера характеризуется достаточным качеством, то модель GRPhitech = f(CD) применима для данного кластера. В случае если параметры, позволяющие оценить качество уравнения ключевой факторной пары кластера, свидетельствуют о низком качестве описания зависимости полученным уравнением, то модель GRPhitech = f(CD) применять для данного кластера нельзя. Далее формулируется вывод о применимости модели FINE. Если уравнение ключевой факторной пары кластера и уравнения промежуточных факторных пар характеризуются достаточным качеством, то модель FINE применима для данного кластера. В противном случае опираться на результаты модели FINE нельзя, так как она не является достоверной для такого кластера. Критериями качества уравнений можно считать: коэффициент детерминации (когда он превышает 50 %), факт достоверности уравнения в целом, факт того, что коэффициент уравнения является статистически значимым.

В рамках кластерного анализа проранжируем регионы РФ по величине валового регионального продукта от наибольшего значения к наименьшему для двух измерений (2011 и 2017 г.). Предполагается корректировка значений ВРП субъектов с целью исключения воздействия инфляционного фактора (базовым годом будет – 2011 г.). Кластерный анализ проведем на основе совокупности, состоящей из 81 региона без учета регионов, данные по которым отсутствовали в 2011 г., и регионов-«выбросов» (г. Москва, г. Санкт-Петербург). Представленную совокупность субъектов РФ разделим на три кластера (по 27 регионов в каждом кластере): первый, второй, третий. По результатам сортировочных итераций формируется итоговый массив данных. Первые 27 отсортированных регионов формируют первый кластер (регионы с высоким уровнем экономического развития). Следующие 27 регионов формируют второй кластер (регионы со средним уровнем экономического развития). Оставшиеся 27 субъектов РФ – третий кластер (регионы с низким уровнем экономического развития). Сортировку регионов по убыванию указанных признаков произведем в программе Excel. Сформированные региональные кластеры по выбранным признакам представлены в табл. 1.

Таблица 1

Группировка регионов по уровню экономического развития

Как видно из табл. 1, за период с 2011 по 2017 г. первый кластер претерпел следующие изменения. Его покинула, переместившись во второй кластер в 2017 г., Республика Коми, при этом первый кластер в том же 2017 г. пополнился Саратовской областью, перешедшей из второго кластера. Во второй кластер из третьего за анализируемый период переместились Тамбовская, Астраханская области и Ненецкий автономный округ. Что касается третьего кластера, то он пополнился также тремя регионами, мигрировавшими из второго кластера: Смоленской, Брянской и Амурской областями.

Следующий этап предполагает формирование числовых рядов вышеуказанных переменных (CD, NC, OL, NLR, GRPhitech) для 2011 и 2017 гг. по каждому кластеру. Полученные числовые ряды для каждого кластера формируют информационную базу значений признаков ключевой факторной пары и промежуточных факторных пар. В рамках данного этапа проведем корреляционный и регрессионный анализ в отношении полученного массива данных. Результаты корреляционного и регрессионного анализа представлены в табл. 2. После чего проверим для каждого кластера выполнение условий, подтверждающих достоверность модели GRPhitech = f(CD) и модели FINE. Исходные данные и результаты проверки отражены в табл. 3.

Таблица 2

Результаты корреляционного и регрессионного анализа факторной системы исследуемых кластеров

Примечание. **Корреляция значима на уровне 0,01 (2-сторон.).

Таблица 3

Результаты проверки достоверности моделей для кластерных совокупностей

Во всех представленных уравнениях коэффициенты являются статистически значимыми, а сами уравнения достоверными. Тем не менее, как видно из табл. 2 и 3, коэффициент детерминации уравнения, описывающего факторную пару «NLR>GRP hitech» для второго кластера, весьма низкий (0,387 – в 2011 г. и 0,465 – в 2017 г.). Также ниже нормативного значения коэффициент детерминации уравнения, описывающего факторную пару «CD>NC» для второго кластера в 2017 г. Все это свидетельствует об ослаблении выявленных факторных связей, иллюстрирующих цепочку перераспределения капитала в высокотехнологичный ВРП, в регионах со средним уровнем экономического развития. На основании этого можно считать, что модель FINE не является достоверной для описания зависимости высокотехнологичного ВРП от факторов интенсивного роста в отношении регионов, объединенных по экономическому развитию во второй кластер. Таким образом, использование модели FINE в качестве методологического инструмента планирования результатов управленческих мероприятий, направленных на стимулирование ВРП за счет усиления воздействия отдельных интенсивных финансовых факторов в отношении регионов второго кластера, может привести к ошибкам прогноза. Следует отметить достаточное качество модельных уравнений, описывающих процесс трансформации регионального финансового капитала в высокотехнологичный ВРП, для первого и третьего кластеров. Как показал проведенный анализ, модель FINE адекватна для регионов первого и третьего кластеров. Она может быть использована в процессе планирования стратегических инициатив, ориентированных на стимулирование роста высокотехнологичного ВРП за счет усиления отдельных интенсивных факторов. Что касается модели, описывающей зависимость высокотехнологичного ВРП от экстенсивных факторов GRPhitech = f(CD) в отношении регионов первого, второго и третьего кластеров, то данная модель характеризуется достаточным уровнем качества и может применяться при планировании стратегии развития региона.

Выводы

Проведенный анализ показал, что дифференциация экономического развития субъектов РФ обуславливает ослабление зависимости высокотехнологичного ВРП от интенсивных финансовых факторов для регионального кластера, включающего регионы со средним уровнем экономического развития. С учетом моделей GRPhitech = f(CD) и FINE, представленных в работах [8,9] с целью стимулирования производства высокотехнологичного сегмента ВРП в регионах с высоким и низким уровнем регионального экономического развития целесообразно проводить следующие стратегические и тактические мероприятия:

– мероприятия, направленные на повышение в регионе объема клиентских средств, привлеченных системой коммерческих банков;

– мероприятия, направленные на повышение интенсивности процесса перераспределения клиентского капитала, привлеченного кредитными организациями, в инструменты кредитной экспансии – новые кредиты;

– мероприятия, направленные на повышение интенсивности годового обновления ссудной задолженности за счет выдачи новых кредитов;

– мероприятия, направленные на повышение эффективности кредитования через формирование качественной (непросроченной) ссудной задолженности на всех этапах кредитного процесса;

– мероприятия, направленные на стимулирование процесса генерации высокотехнологичного сегмента ВРП за счет ссудного капитала, предоставленного эффективным хозяйствующим субъектам.

Таким образом, с помощью регрессионного анализа была подтверждена гипотеза о существовании прямой факторной связи между объемом высокотехнологичного валового регионального продукта и величиной клиентских средств в банках для региональных кластеров, сгруппированных по уровню экономического развития. Что касается гипотезы о существовании опосредованной факторной связи между указанными выше параметрами, то она подтвердилась для субъектов РФ с высоким и низким уровнем экономического развития. Разработанный в работах [8] и [9], методический аппарат можно использовать для обоснования рекомендаций и инициатив, направленных на реализацию роста GRPhitech в регионах первого и третьего кластеров – за счет экстенсивных и интенсивных факторов, а для регионов второго кластера – только за счет экстенсивных факторов.

Исследование было выполнено в рамках гранта РФФИ № 18-010-00909А. Тема: «Инновационное развитие национальной финансовой системы с учетом волатильности мирового рынка капитала в условиях экономики знаний».