Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,798

Полноценное исследование экономического развития страны и ее регионов невозможно без подробного анализа тенденций промышленного развития. В этом плане изучение статистических показателей, характеризующих промышленное производство, опирающееся на применение информационных технологий и экономико-математических методов и моделей, дает возможность не только оценить общую картину развития, но и позволяет определить важнейшие связи показателей и направления их взаимного влияния. В свою очередь, на основе построенных моделей взаимозависимости можно делать математически обоснованные выводы и прогнозы будущего развития.

Цель исследования: экономико-математический анализ взаимосвязей важнейших показателей, характеризующих социально-экономическое развитие регионов и государства в целом. При этом основное внимание в проводимом исследовании уделяется показателям промышленного производства в связи с их ключевой ролью в формировании экономической базы. Выявление взаимозависимостей и сложившихся на данном этапе тенденций изменения показателей является непременным условием разработки долгосрочных стратегических программ экономического развития и определения необходимых внутриполитических мер для получения оптимального результата, генеральным образом выражающегося в достижении уверенной динамики устойчивого развития.

Материалы и методы исследования

Материалом для данного исследования послужили статистические данные о важнейших показателях социально-экономического развития федеральных округов Российской Федерации и страны в целом, опубликованные Росстатом РФ. В качестве методов исследования применялись различные методы обработки и анализа статистических массивов, в частности методы сопоставления и группировок, корреляционный и регрессионный анализ, методы экономико-математического моделирования.

Результаты исследования и их обсуждение

В качестве одного из важнейших показателей экономического развития традиционно рассматривается валовой региональный продукт (ВРП), величина которого в обобщенном виде характеризует процесс производства в регионе товаров и услуг для конечного использования [1]. Исследование корреляции между величиной ВРП и объемами промышленного производства позволяет получить представление о наиболее вероятных направлениях изменения ВРП при перспективных вариациях основных видов промышленных производств.

Построенные на основе официальных статистических данных [2] за 2005–2015 гг. регрессионные модели дают основание утверждать наличие такой связи не только в целом для Российской Федерации, но и для каждого отдельно взятого региона. В частности, локальная проверка влияния обособленно выделенного показателя объема производства, рассчитанного как совокупность объемов производств трех важнейших направлений промышленности (добыча полезных ископаемых, обрабатывающие производства и производство и распределение электроэнергии, газа и воды), показала хорошие результаты достоверности моделей, подтверждаемые нулевыми значениями вероятностей выполнения нуль-гипотез для коэффициента детерминации и для коэффициента регрессии для всех построенных моделей. Результаты расчетов приведены в табл. 1.

Как видно из табл. 1, для всех территорий подтверждается прямая и тесная корреляция между ВРП и объемами промышленного производства, причем для всех регионов, за исключением Уральского, значимый коэффициент регрессии имеет величину больше единицы, что означает, что увеличение объема производства на единицу (в данном случае, на 1 млн руб.) приводит к увеличению ВРП больше, чем на единицу (млн руб.).

Переход от линейных регрессионных моделей к нелинейным (в данном случае логарифмическим) позволяет провести экономическую интерпретацию полученных результатов в терминах не абсолютных единиц измерения (млн руб.), а относительных ( %). При хороших показателях значимости и достоверности всех моделей (нулевые вероятности выполнения нуль-гипотез для коэффициентов детерминации и регрессии) найденные регрессионные коэффициенты (табл. 2) характеризуют изолированное влияние объема производства в каждом федеральном округе на изменение величины его ВРП.

Таблица 1

Регрессионные модели зависимости ВРП от объемов промышленного производства по регионам РФ

Таблица 2

Нелинейные регрессионные модели зависимости ВРП от объемов промышленного производства по регионам РФ

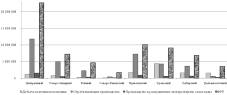
Рис. 1. Величины ВРП и объемов производств по регионам РФ в 2015 г.

Исходя из полученных результатов, можно констатировать, что в течение рассмотренного периода в среднем по стране увеличение объема производства на 1 % приводило к увеличению ВРП на 1,0166 %. Для 95 %-ного уровня значимости это влияние колеблется в пределах от 1,01526 % до 1,01798 %. На 99 %-ном уровне значимости нижняя и верхняя границы интервала данного коэффициента равны 1,01469 % и 1,01856 % соответственно.

Аналогичным образом относительно средних значений коэффициента регрессии, приведенного в табл. 2 для каждого федерального округа, можно построить доверительные интервалы на 95 %-ном и 99 %-ном уровнях значимости.

Однако детальный анализ воздействия различных видов производства на ВРП представляет, пожалуй, больший интерес, поскольку выявляет более конкретную картину и позволяет разрабатывать более конкретные рекомендации по развитию регионов. На статистической базе 2005–2015 гг. авторами был проведен экономико-математический анализ для показателей объемов промышленного производства, официально подразделяемых на три основных вида: добыча полезных ископаемых; обрабатывающие производства; производство и распределение электроэнергии, газа и воды. Общая тенденция связи ВРП и перечисленных производственных показателей для федеральных округов (с учетом вхождения Крыма в состав Южного ФО с 2014 г.) оказалась за исследуемый период довольно устойчивой. Иллюстративный пример соотношения анализируемых показателей за 2015 г. приведен на рис. 1.

Из рис. 1 видно, что доля добычи ископаемых в Уральском ФО заметно выше, чем в остальных округах; что, на наш взгляд, объясняет превышение сумм по объемам производств над ВРП в данном регионе. Лидером в обрабатывающей сфере, как и в сфере производства и распределения электроэнергии, газа и воды, является Центральный ФО, что, впрочем, объясняется не только достаточно большим числом производственных предприятий в регионе, но и высокой концентрацией головных офисов предприятий именно в центре.

При этом вклад различных видов производств в ВРП региона неодинаков не только по федеральным округам, но и по видам производств. Это объясняется как спецификой промышленного развития разных регионов, так и особенностями наполнения ВРП в каждом федеральном округе [3]. В целом, чем выше коэффициент регрессии в уравнении зависимости ВРП от объемов производства, тем больше растет ВРП при единичном увеличении объема конкретного вида производства. Результаты проведения регрессионно-корреляционных вычислений приведены в табл. 3.

Таблица 3

Регрессионные модели зависимости ВРП от объемов промышленного производства по видам для регионов РФ

Таблица 4

Нелинейные регрессионные модели зависимости ВРП от объемов промышленного производства по видам для регионов РФ

Найденные регрессионные зависимости по ранее выделенным видам (добыча полезных ископаемых; обрабатывающие производства; производство и распределение электроэнергии, газа и воды) имеют хорошие параметры качества моделей и демонстрируют изолированное влияние увеличения объема производства на рост ВРП для всех рассмотренных регионов. Во всех случаях найденная связь является прямой и тесной.

В табл. 4 приведены результаты исследования зависимости ВРП от различных видов промышленного производства для нелинейных (логарифмических) моделей, позволяющих перейти от абсолютных показателей к относительным.

Приведенные в табл. 4 коэффициенты нелинейной регрессии показывают уже не денежные, а процентные соотношения изменений ВРП и объемов производства, что, вероятно, является более удобной формой для анализа влияния и выработки рекомендаций для дальнейшего развития промышленности каждого региона. Построенные по исходным статистическим данным логарифмические модели, так же как и предыдущие, обладают всеми признаками качества и демонстрируют сильную и прямую связь между ВРП и объемами производства по видам.

По данным табл. 4 можно сделать несколько условные (с учетом исключения из уравнения константы), но позволяющие определить основные соотношения выводы. Так, если говорить в целом по РФ, то увеличение добычи полезных ископаемых на 1 % приводит к росту ВРП на 1,11 %; рост объемов обрабатывающих производств на 1 % увеличивает ВРП на 1,04 %; повышение объемов производства и распределения электроэнергии, газа и воды на 1 % приводит к увеличению ВРП на 1,16 %. Соответствующие строки в табл. 4 показывают подобные соотношения для каждого из федеральных округов. На основе полученных уравнений, а также имеющейся к настоящему времени динамики развития разных видов производств (рис. 2), можно делать выводы о необходимости и сравнительной эффективности развития различных видов промышленного производства с точки зрения их вклада в ВРП.

Сопоставление результатов различных этапов анализа динамики и взаимосвязей показателей социально-экономического развития дает возможность определить как текущее положение каждого из регионов, так и экономические взаимоотношения регионов и центра, влияющие на формирование экономической картины в стране [4]. Выводы из подобного анализа, опирающиеся на построенные математические модели, несомненно, могут являться важной частью дальнейшего исследования современного развития регионов, необходимой модификации и оптимизации моделей управления экономикой регионов [5].

Динамика объемов производства по выделенным видам деятельности свидетельствует, что в последние полтора десятилетия наиболее высокие темпы роста демонстрируют обрабатывающие производства, что является несомненно позитивной тенденцией по сравнению с временами преимущественного развития отраслей, специализирующихся на добыче полезных ископаемых. Однако при этом увеличение ВРП от вложения средств в обрабатывающие производства – самое низкое по сравнению с другими видами деятельности. Характерно, что большая отдача от добычи полезных ископаемых по сравнению с обрабатывающими производствами наблюдается во всех регионах, за исключением Уральского. Это, вероятнее всего, свидетельствует о более высокой технологической организации работы в сфере обрабатывающих производств в Уральском регионе. Впрочем, необходимо признать, что промышленный потенциал Урала, закладывавшийся еще в петровские времена и укреплявшийся все последующие годы (даже в годы Великой Отечественной войны, когда Урал стал основной базой эвакуируемых из других областей производств), действительно выше большинства регионов страны.

Невысокие темпы роста объемов производства и распределения электроэнергии, газа и воды компенсируются довольно значительным вкладом в рост ВРП увеличения вложений в эту отрасль: в среднем при увеличении объема производства в денежном выражении на 1 (млн руб.) ВРП вырастает на 5,89 (млн руб.). Переход к относительному оцениванию (логарифмическая модель) также подтверждает достаточно высокую эффективность инвестирования этой отрасли: увеличение объема производства на 1 % влечет рост ВРП в среднем на 1,16 %.

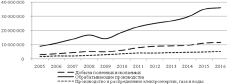
Рис. 2. Динамика объемов производств по видам в целом по РФ

Заключение

В целом использование экономико-статистических методов исследования экономических процессов при условии использования репрезентативных статистических данных позволяет не только проиллюстрировать сложившиеся тенденции развития, но и конкретизировать оптимизационное влияние на них за счет получения в ходе анализа достаточно строгих математических оценок. Разработка стратегий развития для каждого региона – и всей страны как общности ее регионов – должна проводиться с непременным использованием современного математического инструментария, соответствующего целям и условиям проводимого исследования, в целях увеличения эффективности определения средств и методов развития.