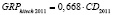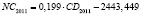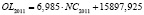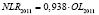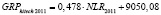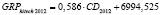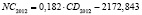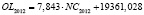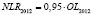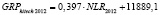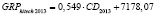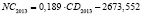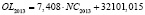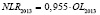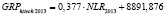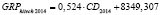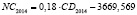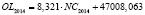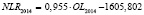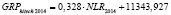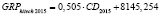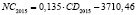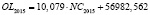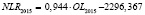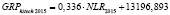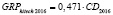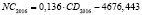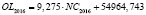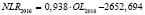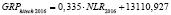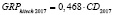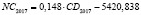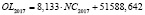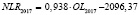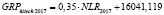Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Исследование факторов экстенсивного и интенсивного роста инновационной компоненты региональной экономической системы в условиях экономики знаний является важной научной задачей. Проблемам социально-экономического развития субъектов РФ, обусловленного влиянием инновационных и экономических процессов под воздействием интенсивных факторов, посвящены работы С.В. Арженовского и Р.В. Шеховцова, Т.А. Балиной и З.В. Пономаревой, М.Ю. Мишиной [1–3]. Ряд исследователей в качестве факторов интенсивного развития регионов выделяет факторы, обеспечивающие реализацию процесса перераспределения финансовых ресурсов в рамках территориального кредитного механизма [4–6].

Тем не менее отмеченные научные работы не дают полного ответа на то, каким образом те или иные финансовые факторы влияют на процесс формирования высокотехнологичного сегмента валового регионального продукта. Учитывая слабую разработанность данной темы, развитие методических аспектов детального анализа факторной связи, характеризующей процесс трансформации финансового капитала в высокотехнологичный сегмент ВРП, следует считать его актуальным и перспективным направлением научных исследований.

Цель исследования: разложение факторной композиции (декомпозиционный анализ), описывающей процесс трансформации финансового капитала в высокотехнологичный сегмент ВРП, на характеризующие промежуточные подпроцессы факторные пары (зависимые и независимые переменные), и проверка гипотезы о наличии взаимосвязей между выявленными факторными парами. В случае подтверждения гипотезы планируется формализовать полученные результаты в виде модели, описывающей влияние финансовых факторов на интенсивность процесса трансформации капитала в высокотехнологичный сегмент ВРП.

Теоретические аспекты и методы исследования

Ранее в работе «Методические аспекты анализа зависимости валового регионального продукта высокотехнологичных отраслей от финансовых факторов в условиях экономики знаний» [7] была подтверждена гипотеза о наличии непосредственной факторной связи между объемом высокотехнологичного валового регионального продукта (GRPhitech) и величиной регионального финансового капитала (CD), привлекаемого и перераспределяемого с помощью системы коммерческих банков. Проведенные в той работе расчеты позволили определить тип уравнения парной регрессии:

GRPhitech = MGRP hitech•CD + cGRP hitech.

В результате проверки гипотезы были сформированы модельные уравнения для каждого года, описывающие факторную взаимосвязь между переменными:

GRPhitech 2011 = 0,668•CD2011,

GRPhitech 2012 = 0,586•CD2012 + 6994,525,

GRPhitech 2013 = 0,549•CD2013 + 7178,07,

GRPhitech 2014 = 0,524•CD2014 + 8349,307,

GRPhitech 2015 = 0,505•CD2015 + 8145,254,

GRPhitech 2016 = 0,471•CD2016,

GRPhitech 2017 = 0,468•CD2017.

Полученные в работе [7] модельные уравнения показали, что экстенсивный рост высокотехнологичного валового регионального продукта может быть достигнут за счет увеличения капитала, привлеченного системой коммерческих банков. Что касается факторов интенсивного роста, то они обобщенно представлены в виде мультипликатора трансформации регионального финансового капитала в высокотехнологичный общественный продукт (MGRP hitech) [7]. В связи с этим закономерен вопрос о детализации факторов, влияющих на изменение мультипликатора и тем самым определяющих интенсивность процесса трансформации. Чтобы понять, какие управленческие мероприятия могут поспособствовать росту интенсивности процесса трансформации финансового капитала в высокотехнологичный ВРП, необходимо, прежде всего, идентифицировать формирующие его промежуточные финансово-экономические процессы (подпроцессы) и выявить их взаимообусловленность. Чем точнее будет исследована факторная композиция (система) процесса трансформации по подпроцессам, тем более полными будут знания о мультипликаторе трансформации и более эффективным будет управление данным процессом.

Сформулируем предположение о том, что интенсивность процесса трансформации финансового капитала в высокотехнологичный ВРП зависит от характера реализации цепи следующих подпроцессов:

а) трансформации финансовых ресурсов, которые привлечены кредитными организациями, в новые кредиты, выдаваемые хозяйствующим субъектам;

б) процесса оборачиваемости годового объема выданных кредитов в базовом активе банковской системы – ссудной задолженности хозяйствующих субъектов;

в) процесса эффективного размещения ссудной задолженности через кредитование хозяйствующих субъектов, степень эффективности которого определяется величиной чистой ссудной задолженности и потерями от возникновения просроченной ссудной задолженности;

г) процесса стимулирования высокотехнологичного общественного воспроизводства за счет использования ссудного капитала (рисунок).

Проверка сформулированного выше предположения осуществляется методом стохастического факторного анализа. С целью количественного описания анализируемых явлений и факторов введем следующие переменные:

CD – среднегодовой объем средств клиентов, привлеченных коммерческими банками на территории субъекта РФ;

NC – среднегодовая величина кредитов, выданных кредитными организациями физическим и юридическим лицам (экономическим субъектам), осуществляющим свою деятельность на территории региона РФ;

OL – среднегодовая величина совокупной ссудной задолженности физических и юридических лиц (экономических субъектов), осуществляющих свою деятельность на территории региона РФ, перед кредитными организациями;

NLR – среднегодовая величина чистой ссудной задолженности физических и юридических лиц (экономических субъектов), осуществляющих свою деятельность на территории региона РФ, перед кредитными организациями;

GRPhitech – объем производства высокотехнологичных отраслей, входящий в ВРП субъекта РФ.

Объектом анализа выступает факторная система, предполагающая цепную обусловленность входящих в нее факторов (CD > NC > OL > NLR > GRPhitech). Планируемый алгоритм проведения стохастического анализа представлен на рисунке.

Информационной основой послужили ряды данных по указанным выше переменным в региональном разрезе за 2011–2017 гг. Полученные данные были подвергнуты корректировкам: 1) были исключены регионы, значения которых можно отнести к статистическим «выбросам» (г. Москва, г. Санкт-Петербург), и регионы, по которым имеются неполные данные для выбранного временного промежутка (г. Севастополь, Республика Крым); 2) исключение инфляционного фактора (базисным годом был принят 2011, данные последующих лет были очищены по каждому региону с учетом годовой инфляции, характерной для того или иного субъекта РФ). Количество наблюдаемых субъектов РФ составило 81.

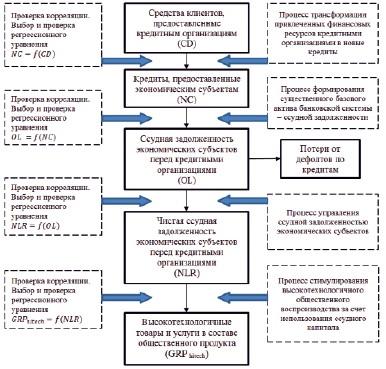
Схема факторной системы, описывающей процесс трансформации финансового капитала в высокотехнологичный общественный продукт

Проведенный с использованием программного продукта SPSS 17 корреляционный анализ по всем факторным парам (CD → NC; NC → OL; OL → NLR; NLR → GRPhitech) подтвердил наличие прямой и весьма высокой (по шкале Чеддока) связи между факторами. Результаты анализа представлены в табл. 1. Было сформулировано предположение, что исследуемые связи между факторами описываются формулой парной регрессии типа: Y = aX + b, где Y – зависимая переменная, Х – независимая переменная факторной пары, a – коэффициент регрессии, b – константа.

Как видно из табл. 1, коэффициент детерминации всех полученных моделей превышает 0,85, что свидетельствует о достаточно высокой точности описания связи между переменными. Проверка достоверности с помощью p-значения p(F)установила, что данный критерий меньше уровня значимости α (0,05), поэтому нулевая гипотеза о незначимости всех представленных уравнений линейной регрессии отвергается. Р-значение для коэффициента регрессии во всех уравнениях меньше 0,05, что свидетельствует о его статистической значимости. В тех уравнениях, в которых критерии качества подтверждают то, что константа является статистически незначимой, данный элемент модели опускается.

Результаты исследования и их обсуждение

По итогам регрессионного анализа были сформулированы уравнения зависимости факторов по годам. Объединим эти уравнения с ранее полученными в статье [7] моделями, описывающими ключевую факторную пару GRP_hitech = f(CD). Результаты представим в табл. 2.

Таблица 1

Результаты корреляционного и регрессионного анализа факторной системы, описывающей процесс трансформации финансового капитала в высокотехнологичный общественный продукт

Примечание. **Корреляция значима на уровне 0,01 (2-сторон).

Таблица 2

Уравнения, описывающие поведение факторной системы

Так как известны уравнения факторной цепи (CD >NC >OL >NLR > GRPhitech), зависимость объема высокотехнологичной продукции и услуг от финансового капитала, привлеченного кредитными организациями (CD > GRPhitech), можно выразить не напрямую через уравнение ключевой факторной пары, а опосредованно через уравнения регрессии промежуточных факторных пар. Однако в силу того, что полученные модели не на 100 % аппроксимируют выявленные зависимости, в реальности подобное опосредованное выражение будет иметь не тождественное равенство, а приблизительное:

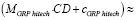
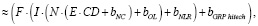
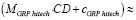
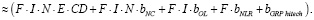
Исходя из полученных выражений, приблизительное равенство выполняется и для их производных:

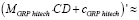
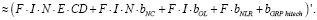
Так как MGRPhitech, F, I, N, E, bNC, bOL, bNLR, bGRP hitech, cGRP hitech соответствуют определенным фиксированным числовым значениям, а CD – зависимая переменная, то итоговый результат нахождения производной будет следующим:

M _{GRP hitech} ≈ F•I•N•E.

Таблица 3

Переменные модели FINE

Таблица 4

Значения переменных модели FINE с 2011 по 2017 г.

На основании этого допущения введем модель, которую условно обозначим как «FINE». Указанная модель характеризует ту компоненту трансформационного потенциала, которая описывается переменными F, I, N, E. Иными словами мы получили модель интенсивного роста высокотехнологичного валового регионального продукта за счет регионального финансового капитала, перераспределяемого с помощью системы коммерческих банков.

M _{GRP hitech} ≈ M _{GRP hitech FINE},

M _{GRP hitech FINE} = F•I•N•E.

Проведенный декомпозиционный анализ позволил выявить факторы, влияющие на интенсивность процесса трансформации регионального финансового капитала в высокотехнологичный общественный продукт, и получить модель FINE, иллюстрирующую воздействие этих факторов.

В табл. 3 представлены характеристики переменных, входящих в модель FINE, и диапазон их возможных значений. Оценим влияние факторов модели FINE в формировании модельного коэффициента MGRP hitech FINE. Результаты представим в табл. 4. Как видно из данных табл. 4, несмотря на рост интенсивности годового обновления ссудной задолженности (с 6,985 в 2011 г. до 8,133 в 2017), происходящее снижение интенсивности процесса трансформации привлеченного банками клиентского капитала и сокращение интенсивности процесса стимулирования генерации высокотехнологичного сегмента ВРП привели к уменьшению модельного коэффициента MGRPhitech FINE (с 0,623 в 2011 г. до 0,395 в 2017 г.).

Выводы

Таким образом, гипотеза о наличии взаимосвязей между выявленными факторными парами для исследуемой совокупности регионов подтверждается. На основе полученных результатов была сформирована модель, объясняющая факторную зависимость мультипликатора, который иллюстрирует интенсивность процесса трансформации регионального финансового капитала в высокотехнологичный общественный продукт. Было установлено, что интенсивный рост трансформации регионального финансового капитала в высокотехнологичный общественный продукт зависит от следующих факторов:

а) интенсивности процесса трансформации привлеченного банками клиентского капитала в инструменты кредитной экспансии – новые кредиты;

б) скорости обновления ссудной задолженности за счет выданных новых кредитов;

в) эффективности процесса кредитования – формирования эффективной (непросроченной) ссудной задолженности на базе совокупной ссудной задолженности;

г) интенсивность стимулирования генерации высокотехнологичного сегмента ВРП за счет ссудного капитала, вложенного в эффективные хозяйствующие субъекты.

Сформулированная в работе модель представляет собой дополнительный методологический инструмент декомпозиционного анализа и может быть использована в аналитической работе при планировании сценарных моделей инновационного и финансового развития регионов в рамках интенсивного пути развития.

Исследование было выполнено в рамках гранта РФФИ № 18-010-00909А. Тема: «Инновационное развитие национальной финансовой системы с учетом волатильности мирового рынка капитала в условиях экономики знаний».