Дисциплина Эконометрика является обязательной дисциплиной для студентов бакалавриата, обучающихся по направлению Экономика. Написано много хороших учебников, разработаны онлайн-курсы разной степени сложности. В большинстве учебных программ и созданных в соответствии с ними учебных пособиях и учебниках отсутствуют темы, посвященные предварительному анализу данных, используемых при эконометрическом моделировании. В последнее время быстрыми темпами растет количество новых методов прикладной статистики и их реализация в виде функций свободного программного обеспечения, такого как Gretl и R. У преподавателей появилась возможность сопровождать изучаемые темы решением задач на реальных данных. Однако доступность огромных объемов данных и хорошего инструментария делает все более необходимым предварительный анализ данных [1]. Потому что качество модели регрессии может в значительной мере зависеть от характера наблюдений или наличия выбросов. Различные способы определения, идентификации и обработки выбросов существенно изменяют выводы исследования, поэтому задача выявления необычных наблюдений является важной.
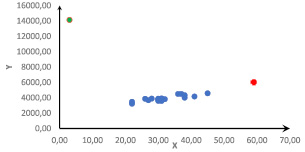
Рис. 1. Диаграмма рассеяния
Материалы и методы исследования
В статье рассматриваются возможности программы R [2] для решения одной из задач предварительного анализа данных, а именно задачи обнаружения влиятельных наблюдений и выбросов при построении модели линейной регрессии.
При анализе наблюдений выделяют три типа необычных наблюдений [3]:
- наблюдение представлено необычным сочетанием значений экзогенных переменных (англ. leverage point), это выбросы в отношении других независимых переменных;
- влиятельное наблюдение оказывает существенное влияние на оценки параметров модели (англ. influential point или influential observation), удаление такого влиятельного наблюдения из выборки приведет к значительному изменению предсказываемых моделью значений;
- выброс (англ. outlier) – наблюдение эндогенной переменной, резко отличающееся от других наблюдений. К выбросам относятся аномальные наблюдения, лежащие в стороне от регрессионной зависимости для большинства других наблюдений.
Влиятельные наблюдения обладают как минимум одним из двух указанных выше свойств (т. е. являются либо «leverage point», либо «outlier»), но чаще всего сочетают их.
Результаты исследования и их обсуждение
Обнаружение влиятельных наблюдений и выбросов рассмотрим на данных примера о количестве выпущенных изделий и затратах. Диаграмма рассеяния этих данных приведена на рис. 1.
Для изучения выбросов и влияния отдельных наблюдений в регрессионном анализе предложено большое количество статистических тестов [3, 4].
Показатель воздействия наблюдения или «разбалансировки» (leverage)
В литературе показатель влияния обозначается обычно hii – этот символ происходит из матричной формы записи, где hii является диагональным элементом матрицы H (hat matrix). Для пояснения матрицы Н напомним, что вектор оценок регрессионных коэффициентов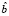 
регрессионной модели Y = Xb получают следующим образом:
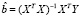, откуда предсказываемые моделью значения эндогенной переменной можно записать как 
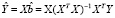. Выражение X(XTX)-1XT обозначают через H, т.е. 
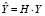или
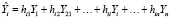for i = 1,…n.
Рычаг (leverage), hii, количественно определяет влияние Yi на его предсказанное значение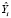 
. Диагональные элементы матрицы проекции Н изменяются от 0 до 1 и отражают силу воздействия отдельных наблюдений на оценки регрессионных коэффициентов. Чем дальше то или иное наблюдение находится от центра многомерного распределения значений регрессоров, тем выше будет соответствующий диагональный элемент. К классу «leverage point» относят наблюдения с большими значениями hii. Правило, по которому определяют, оказывает ли некоторое наблюдение существенное влияние на параметры модели – 
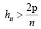[5]. В нашем примере критическое значение hii > 0.2105. Не все наблюдения, которые можно отнести к классу «leverage point», являются влиятельными.
Рычаг (leverage), hii в R можно получить несколькими способами:
hat(X) # Способ 1
diag(H) # Способ 2
Minf <- influence(Model) # Способ 3
Minf$hat
В приведенном ниже протоколе два наблюдения 10 и 19 имеют леверидж больше 0.2105.
> # Способ 3:
> model <- lm(y~ x)
> Minf <- influence(Model)
> Minf$hat
1 2 3 4 5 6 7 8
0.09665815 0.05424595 0.06825712 0.05299157 0.06021017 0.05424595 0.09665815 0.12986368
9 10 11 12 13 14 15 16
0.06939316 0.42807441 0.05424595 0.06939316 0.08991290 0.06340528 0.05945281 0.05299157
17 18 19
0.06435198 0.05263656 0.38301146
На первом этапе мы выявили два наблюдения (10 и 19) с высоким потенциалом воздействия на параметры модели.
Выбросы, резко отличающиеся наблюдения эндогенной переменной
Рассмотрим диаграмму рассеяния (корреляционное поле), отражающую взаимосвязь исследуемых переменных (рис. 1). Можно предположить, что зеленая точка, соответствующая 10 наблюдению, является выбросом, аномальным наблюдением. Построим два уравнения регрессии. Первое по всем наблюдениям и второе – исключив 10 наблюдение. Графики этих двух уравнений приведены на рис. 2, основные характеристики моделей приведены в табл. 1.
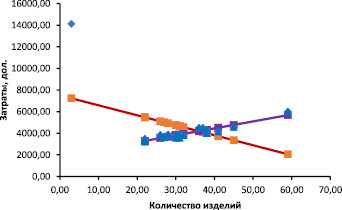
Рис. 2. Две линии двух регрессий: с учетом 10 наблюдения и без него
В первом уравнении даже знак минус при коэффициенте b1 противоречит экономическому смыслу задачи. Стандартная ошибка при коэффициенте b1 в 7 раз больше в первой модели, а стандартная ошибка модели 1 почти в 10 раз больше стандартной ошибки второй модели. Наличие аномального значения 10 наблюдения связано с влиянием на признак редкого события – на фабрике был пожар, в результате которого резко возросли затраты на ликвидацию последствий.
Таблица 1
Сравнительные характеристики двух моделей
|
b0 |
b1 |
Стандартная ошибка b1 |
Стандартная ошибка модели |
Коэффициент детерминации R2 |
|
|
1 модель |
7513.02 |
–92.29 |
47.13 |
2222.53 |
0.18 |
|
2 модель |
1882.44 |
64.35 |
6.30 |
230.85 |
0.86 |
Для диагностики выбросов в R в моделях линейной регрессии кроме остатков (residuals)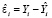 
используются еще два типа остатков:
– стандартизованные остатки (standardized residuals)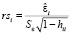 
;
– и стьюдентизированные остатки (studentized residuals), внешний стьюдентизированный остаток (Externally studentized residual) или стьюдентизированный удалённый остаток (Studentized deleted residual):
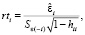
где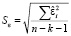 
– стандартная ошибка модели; Sε(–i) – стандартная ошибка модели без i-го наблюдения.
В R для расчета стьюдентизированных остатков служит функция rstudent(), а стандартизованных rstandard().
> rs<-rstandard(model)
> round(rs,3)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
-0.953 -0.445 -0.586 -0.343 0.138 -0.402 -1.071 0.588 0.149 4.102 -0.535 -0.003 0.202 -0.630
15 16 17 18 19
-0.484 -0.498 0.185 -0.345 2.252
> rt<-rstudent(model)
> round(rt,3)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
-0.950 -0.434 -0.574 -0.334 0.134 -0.392 -1.076 0.576 0.144 39.494 -0.523 -0.003 0.196 -0.619
15 16 17 18 19
-0.473 -0.487 0.179 -0.336 2.609
Стандартизованные остатки распределены асимптотически нормально, но имеют разную дисперсию и не учитывают удалённость наблюдения от центра системы. Поэтому величины rsi можно использовать лишь в качестве самых ориентировочных указателей на возможные выбросы. Наблюдения, чьи стандартизованные остатки выходят за пределы диапазона от –2 до 2, можно считать выбросами. В нашем примере это 10 и 19 наблюдения.
Стьюдентизированные остатки имеют t-распределение с n–p степенями свободы. Соответственно, мы можем использовать квантили этого распределения для проверки того, насколько статистически значимо определенное наблюдение является выбросом. Так, в случае с нашим примером мы можем проверить, является ли статистически значимым выбросом наблюдения 10 и 19 с наибольшими (абсолютными) значениями стьюдентизированных остатков.
> abs(qt(.05/(n*2), n-p)) # с поправкой Бонферрони
[1] 3.5193
Как видим, максимальное наблюдаемое значение стьюдентизированного остатка 10 наблюдения (39.494) превышает критическое t-значение = 3.593 (рассчитанное с применением поправки Бонферрони). Поэтому наблюдение 10 является статистически значимым выбросом. Значение следующего по абсолютной величине стьюдентизированного остатка (2.609) не превышает критическое t-значение = 3.593. Из этого следует вывод, что данное наблюдение (№ 19) не является статистически значимым выбросом. Аналогичный вывод справедлив и для других наблюдений (чьи стьюдентизированные остатки еще меньше, чем 3.593).
Влиятельные наблюдения. Расчёт статистик влияния (Influence Statistics)
Наблюдение является влиятельным, если оно вносит существенный вклад в оценки параметров модели. Поэтому самый простой способ измерения степени влиятельности заключается в удалении конкретного наблюдения из выборки и последующем расчете оценок параметров модели без него. Если удаление наблюдения приводит к значительному изменению в оценках тех или иных параметров модели, значит, это наблюдение является влиятельным. Изменения оценок параметров модели можно записать следующим образом:
DFBETAij = bj – bj(–i),
где bj(–i) обозначает оценку j-го параметра модели (т.е. bj), полученную по методу наименьших квадратов после удаления i-го наблюдения (i = 1,…,n, j = 1,…,k).
В программных продуктах и в R, в том числе, приводятся различные статистики влияния. К ним относят: расстояние Кука, ковариационное отношение, DFBETA, DFBETAS, DFFITS и другие [6, 7].
Стандартизованную статистику DFBETASij получают при делении каждого значения DFBETAij на стандартную ошибку соответствующего коэффициента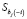 
:
,
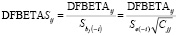где Se(–i) – стандартное отклонение ошибки регрессии при удалении i-го наблюдения, а Cjj – диагональный элемент матрицы (XTX)-1.
Для расчета эти двух статистик в R имеются одноименные функции – dfbeta() и dfbetas().
> model <- lm(y~ x)
> dfbeta(model)
(Intercept) x
1 -433.4521718 9.91350466
2 -81.1218890 0.86606999
3 -185.1361815 3.57751075
4 -51.2959724 0.31526809
5 -1.9839115 0.58615567
6 -73.2741413 0.78228621
7 -487.0777220 11.13997710
8 -189.5894301 8.25599302
9 -11.9738058 0.94103081
10 5630.5803825 -156.64278048
11 -97.4924596 1.04084476
12 0.2636306 -0.02071894
13 -36.7361567 1.92937314
14 -177.7352628 3.18485153
15 -120.4155156 1.94388049
16 -74.5228237 0.45802169
17 -8.7298779 0.97333122
18 -40.2428170 -0.03726187
19 -2142.1234899 77.67874928
Модель 1, построенная по 19 наблюдениям, имеет вид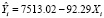 
.
Если теперь удалить 10 наблюдение, которое является выбросом, то уравнение изменится на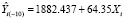 
(модель 2).
Тогда:
DFBETA–b010 = 7513.02 – 1882.437 = 5630.58,
DFBETA–b110 = –92.29 – 64.35 = –156.64.
> dfbetas(model)
(Intercept) x
1 -0.2722868358 2.097392e-01
2 -0.0498710394 1.793207e-02
3 -0.1143124525 7.439610e-02
4 -0.0314601453 6.512151e-03
5 -0.0012132103 1.207240e-02
6 -0.0449977584 1.617979e-02
7 -0.3082665159 2.374539e-01
8 -0.1170696586 1.716985e-01
9 -0.0073229114 1.938306e-02
10 34.1516108339 -3.199893e+01
11 -0.0600925122 2.160739e-02
12 0.0001611256 -4.264845e-04
13 -0.0224794438 3.976263e-02
14 -0.1099190933 6.633698e-02
15 -0.0741085161 4.029231e-02
16 -0.0458833218 9.497703e-03
17 -0.0053408721 2.005541e-02
18 -0.0246820051 -7.697039e-04
19 -1.5630494791 1.908963e+00
Для малых и средних объёмов выборок влиятельными наблюдениями признаются DFBETAS со значениями более 1, а для больших выборок – более 2. Изменения свободного члена и коэффициента регрессии значимы, наблюдения 10 и 19 признаются влиятельным. Изменение свободного члена и коэффициента регрессии приведены на рис. 3.
В R есть функция influence.measures(), которая позволяет одновременно рассчитать все перечисленные выше показатели влиятельности. Замыкает таблицу результатов функции influence.measures(), столбец inf – он содержит звездочки * напротив наблюдений, которые по совокупности всех показателей следует считать влиятельными. В рассматриваемом примере это наблюдения 10 и 19.
Заключение
После проведенного анализа исходных данных на наличие выбросов и влиятельных наблюдений принимается решение о корректировке данных. К удалению выявленных аномальных наблюдений следует относиться с осторожностью, опираясь на содержательный анализ. Так, в рассматриваемом примере только наблюдение 10 можно рекомендовать к удалению. При исследовании данных, представленных временными рядами выявленные выбросы, можно заменить сглаженными значениями.
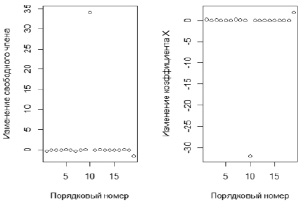
Рис. 3. Изменение свободного члена и коэффициента регрессии
С помощью приведенного примера проиллюстрирован тезис о необходимости предварительного анализа данных при построении эконометрических моделей и важности включения этой темы в рабочие программы дисциплины Эконометрика.