Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Развитие молочной отрасли является одним из приоритетных направлений государственной политики в сфере АПК. Производство молока в России на протяжении ряда лет относительно стабильно, однако наблюдается существенное сокращение поголовья коров, которое компенсируется ростом продуктивности молочного стада. В 2018 г. производство молока в хозяйствах всех категорий составило 30,6 млн т, что на 1,5 % больше чем в 2017 г. За последние пять лет производство молока увеличилось на 2,6 %, а по отношению к 2004 г. – снизилось на 3,8 %. В коммерческом секторе (сельскохозяйственные организации и КФХ) производство молока имеет устойчивую тенденцию к росту (в среднем на 215 тыс. т ежегодно), а в хозяйствах населения, наоборот, сокращается (в среднем на 365 тыс. т в год). По состоянию на 2018 г. производство в хозяйствах населения составило 11,9 млн т или 38,7 % от общего объема.

Проблема прогнозирования социально-экономических процессов, отражающих перспективы развития сельскохозяйственных отраслей страны и ее регионов, является очень важной. В значительной степени это обусловлено тем, что возрастает число предприятий и организаций, эффективность деятельности которых непосредственно зависит от способности предвидеть развитие событий. Большинство методов, используемых для построения прогнозных моделей, исходят из следующих предположений: основные тенденции и зависимости, наблюдавшиеся в прошлом, сохранятся или можно предсказать направление их изменения в будущем; процессы имеют вероятностный характер и развитие исследуемого объекта определяется суммарным влиянием закономерности и случайности.

В практике прогнозирования значительного количества процессов различной природы применяются модели временных рядов. Структура экономических временных рядов может быть настолько сложной, что в результате моделирования трендовой и сезонной компоненты традиционными методами в остаточном ряду остаются статистические зависимости, которые можно моделировать. Для прогнозирования таких процессов используются модели авторегрессии скользящего среднего (ARMA-модели), а в случае нестационарности временного ряда – модели авторегрессии проинтегрированного скользящего среднего, разработанные Дж. Боксом и Г. Дженкинсом (ARIMA-модели) [1].

Материалы и методы исследования

Исследование базируется на использовании статистических данных поквартальных объемов производства молока в Российской Федерации за период с 2004 по 2018 г. Целью работы является построение нескольких адекватных ARIMA-моделей и выбор наиболее подходящей по показателям качества и точности модели для прогнозирования будущих значений исследуемого временного ряда.

В общем виде модель ARIMA(p, d, q) выражается формулой

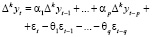
или

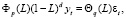
где 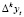– k-я последовательная разность уровней yt;

ε_t – «белый шум»;

р и q – порядок авторегрессии (AR) и порядок скользящей средней (MA);

d – порядок интегрируемости;

L – оператор сдвига, т.е. преобразование ряда, смещающее его на один временной такт;

Φp(L) и Θq(L) – функции операторов лага соответствующих AR(p) и MA(q) процессов.

Модель Бокса – Дженкинса может быть интерпретирована как модель множественной линейной регрессии, в которой в качестве факторных переменных выступают предшествующие значения зависимой переменной, а в качестве регрессионного остатка – скользящие средние из элементов «белого шума».

Использование ARMA-моделей предполагает стационарность временных рядов, а многие экономические временные ряды нестационарны. В большинстве случаев для приведения ряда к стационарному виду достаточно исключить детерминированные компоненты (тренд, периодичность) или применить операцию взятия разности. Способ приведения нестационарного временного ряда к стационарному зависит от того, с каким типом нестационарности мы имеем дело (например, содержит ли ряд детерминистический или стохастический тренд). Во многих случаях получить стационарные временные ряды позволяет взятие d-й последовательной разности: 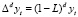. Если ряд становится стационарным после d-кратного взятия разностей, процесс называется интегрируемым d-го порядка. Для сезонных временных рядов с длиной периода s применяется взятие конечных разностей с лагом s:

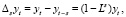
где Ls – оператор сдвига на s периодов. Наиболее распространенным и эффективным из простых тестов на стационарность и порядок интегрируемости является обобщенный тест Дики – Фуллера [2].

Интегрированная модель авторегрессии скользящего среднего (ARIMA-модель) может достаточно хорошо описывать поведение нестационарных временных рядов, в том числе содержащих сезонную компоненту. Модели ARIMA в значительной степени подходят для прогнозирования временных рядов, характеризующих сельскохозяйственное производство, так как эти ряды в силу специфики влияющих факторов являются стохастическими. К тому же временные ряды параметров сельскохозяйственного производства часто являются нестационарными [3, 4].

Результаты исследования и их обсуждение

Анализируемый временной ряд объемов производства молока, как и многие экономические процессы в сельском хозяйстве, обладает сезонной периодичностью. Традиционные подходы моделирования временных рядов с периодическими колебаниями (расчет значений периодической компоненты и построение аддитивной или мультипликативной модели; использование рядов Фурье; применение моделей с переменной структурой [1]), как правило, не являются экономичными в том смысле, что модель может содержать слишком много параметров. Уменьшить число параметров модели временного ряда с периодичностью возможно путем учета при построении прогнозной модели взаимосвязей между уровнями ряда, разделенными периодом колебаний, т.е. построения сезонной модели ARIMA(р, d, q)(P, D, Q)s:

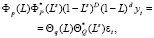
где Р и Q – порядок сезонной авторегрессии и порядок сезонной скользящей средней;

D – порядок сезонной разности.

Определение порядков сезонной авторегрессии AR(P) и сезонного скользящего среднего MA(Q) основано на исследовании диаграмм автокорреляционной (АКФ) и частной автокорреляционной (ЧАКФ) функций, при этом все типичные проявления связаны с сезонными лагами [2, 5].

На этапе идентификации ARIMA-модели необходимо, чтобы ряд первоначально нестационарный стал стационарным. Анализ графика исходного временного ряда, а также диаграмм АКФ и ЧАКФ (рис. 1) дает основания предположить, что ряд нестационарен. Значение автокорреляционной функции практически не убывает по мере роста лагов.

Для подтверждения наших предположений относительно нестационарности анализируемого ряда используем обобщенный тест Дики – Фуллера. При проведении теста необходимо решить проблему включения в тестовое уравнение константы, тренда и числа добавок (лаговых значений зависимой переменной). Так как в ряду производства молока за анализируемый период тренд отсутствует, то нет смысла включать его в тестовое уравнение. Исходя из специфики данных (квартальные), в модель включается четыре лага. Критическое значение t-статистики для модели с константой составляет t0,05 = –2,91. Так как полученное значение t-критерия Стьюдента (–1,89) превышает критическое, с вероятностью 0,95 принимается гипотеза о нестационарности ряда.

Анализируемый временной ряд производства молока содержит ярко выраженную сезонную компоненту с периодом, равным четырем кварталам. Для приведения временного ряда к стационарному виду ряд был преобразован с помощью процедуры взятия сезонных разностей с лагом 4. Тест Дики – Фуллера для сезонной разности ряда показал, что значение t-статистики на 5 %-ном уровне значимости равное –3,92 меньше критического (t0,05 = –1,95), что позволяет сделать вывод о том, что ряд сезонных разностей с вероятностью 95 % стационарен, т.е. исходный ряд имеет первый порядок сезонной интегрируемости: D = 1.

Для выявления наиболее подходящих для описания исследуемого временного ряда моделей были проанализированы различные комбинации параметров p, q, P, Q. Выбор значений порядков авторегрессии и скользящего среднего осуществляли на основе анализа автокорреляционной и частной автокорреляционной функций (рис. 2) [2, 6].

Среди адекватных моделей были выбраны три наиболее подходящие сезонные модели ARIMA(p, d, q)(P, D, Q)s, результаты оценивания которых представлены в табл. 1. Параметры ARIMA-моделей оценивались методом максимального правдоподобия.

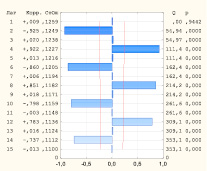
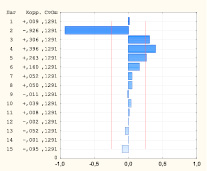
Рис. 1. Автокорреляционная и частная автокорреляционная функции ряда

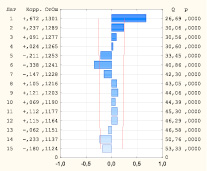
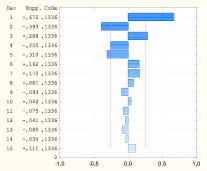
Рис. 2. Автокорреляционная и частная автокорреляционная функции сезонных разностей

Таблица 1

Результаты оценивания ARIMA-моделей

По t-критерию Стьюдента все параметры моделей статистически значимы при 5 %-ном уровне значимости. Для подтверждения того, что построенные модели адекватно описывают исходный временной ряд, проанализируем их остатки. Проверим некоррелированность остатков с помощью теста Бокса – Льюнга [1] (табл. 2).

Так как для разного числа лагов значимость Q-статистики больше 0,05, с вероятностью 0,95 автокорреляция в остатках всех трех ARIMA-моделей отсутствует.

Для проверки нормальности остатков используем тест Харке-Бера (табл. 3). Этот тест вычисляет для остатков модели выборочные значения коэффициентов асимметрии A и эксцесса E. При условии нормальности распределения, статистика Харке-Бера

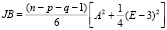
имеет χ2 распределение с двумя степенями свободы.

Распределение остатков для всех моделей соответствует нормальному, так как значимость статистики Харке-Бера больше 0,05. Таким образом, анализ остаточной последовательности свидетельствует об адекватности построенных ARIMA-моделей.

Общими показателями качества модели ARIMA являются критерий Акайка и байесовский критерий Шварца, основанные на принципе снижения остаточной суммы квадратов при добавлении значимого фактора. В табл. 4 для отбора наиболее подходящей для прогнозирования модели представлены критерии Акайка и Шварца, а также показатели точности: средняя абсолютная процентная ошибка и средняя квадратическая ошибка [5].

В результате анализа данных табл. 4 установлено, что построенные ARIMA-модели демонстрируют высокий уровень аппроксимации на фактических данных. Сравнительная оценка моделей на основе информационных критериев и показателей точности приводит к выводу о целесообразности использования для прогнозирования всех трех моделей с последующим усреднением индивидуальных прогнозов. Такой способ объединения прогнозов, полученных от прогнозирования по различным моделям, способствует улучшению результатов, так как учитывается больше информации. В табл. 5 приводится результат расчета прогнозных значений поквартальных объемов производства молока в России на 2019–2020 гг.

Таблица 2

Проверка остатков на наличие автокорреляции в остатках

Примечание. Q-стат. – статистика Бокса – Льюнга; р – оценка значимости Q-статистики.

Таблица 3

Результаты теста Харке-Бера для проверки нормальности распределения

Таблица 4

Сравнительная оценка точности и адекватности ARIMA-моделей

Таблица 5

Результат прогнозирования объемов производства молока в РФ, тыс. т

Согласно долгосрочному прогнозу Минэкономразвития [7] производство молока в РФ в ближайшие годы будет развиваться умеренными темпами – к 2024 г. прирост составит 3,8 % по отношению к 2018 г. При этом основной прирост обеспечит корпоративный сектор, где в последние годы отмечается рост инвестиционных вложений и расширение использования усовершенствованных технологий производства молока. Прогнозные расчеты, проведенные с использованием разработанных ARIMA-моделей (табл. 5), показывают, что производство молока в России в ближайшей перспективе будет увеличиваться, но меньшими темпами. Так, согласно «усредненному» прогнозу в 2019 г. ожидается увеличение производства молока на 0,7 %, а в 2020 г. – на 1,1 % по отношению к уровню 2018 г.

Выводы

Применение стохастических сезонных моделей ARIMA является достаточно эффективным методом краткосрочного и среднесрочного прогнозирования временных рядов с периодичностью, характеризующей изменение показателей сельскохозяйственного производства. Модели авторегрессии проинтегрированного скользящего среднего с сезонностью позволяют достаточно точно аппроксимировать широкий класс случайных процессов, нестационарность которых обусловлена наличием во временных рядах периодической составляющей. Основным недостатком моделей класса ARMA является то, что при добавлении к исходному ряду новой информации, необходимо корректировать модель. При этом значения порядков AR и MA процессов могут значительно измениться, что приведет к построению совершенно другой модели.