Социальные изменения, вызванные третьей технологической революцией, привели к изменениям в использовании городского пространства. Современные города являются узлами концентрации сырья, рабочей силы и основных средств. Логистика, как один из источников постоянного и устойчивого роста эффективности всех подсистем города, является важным элементом управления крупной агломерацией. Отдельной формой логистической деятельности исследователи В.В. Жариков, Н.А. Чайников [1], Е.В. Кейванова [2] выделяют социально-ориентированную логистику, «результаты которой измеряются не только экономическим, но и социальным эффектом в виде общественно значимых последствий этой деятельности» [2]. В качестве системных целей социально-ориентированной логистики называются, например, такие как обеспечение экологической безопасности, проведение государственной геополитики, сохранение флоры и фауны, развитие спорта, оказание помощи дружественным странам, повышение уровня образования и пр. К категории логистической деятельности, изначально ориентированной на получение социального эффекта, авторы также относят и логистику здравоохранения и, в частности, логистику скорой медицинской помощи.
Цель исследования: предложить модель рационального пространственного размещения станций и отделений скорой медицинской помощи в целях полного и своевременного удовлетворения потребностей населения в услугах в условиях новой индустриализации.
Материалы и методы исследования
Материалом для исследования послужили географические координаты зданий г. Екатеринбурга. Для решения задачи оптимального местоположения станций скорой помощи был использован кластерный анализ.
Результаты исследования и их обсуждение
Первые научные исследования и практические разработки в сфере управления логистикой скорой медицинской помощи относятся к середине 1960-х гг. При разработке оптимальных решений для повышения эффективности деятельности скорой медицинской помощи применялись методы математического программирования, теории массового обслуживания, имитационного моделирования и математической статистики, интеллектуального анализа данных.
Наиболее серьезной задачей стратегического и тактического уровня планирования логистической деятельности скорой медицинской помощи является оптимизация расположения станций или отделений скорой помощи в пределах определенного района. Важность решения о наилучшем местоположении обусловлена тем, что результат лечения в экстренных случаях зависит от скорости оказания медицинской помощи и во многих странах в качестве показателей, дающих представление об улучшении состояния больных, часто используют временные параметры работы скорой медицинской помощи, например среднее время доезда.
Задача оптимального местоположения отделений скорой помощи относится к классу задач размещения объектов в заданном пространстве. Подходы к решению таких задач используют четыре характеристики [3]:
- клиенты (точки спроса), расположенные в узлах улично-дорожной сети города;
- объекты обслуживания, также расположенные в узлах улично-дорожной сети города;
- район расположения всех клиентов и объектов;
- метрика, задающая расстояние между узлами или время доезда от одного узла до другого.
В качестве целей задач размещения, как правило, выступают максимизация охвата территории обслуживания, что характерно для моделей покрытия, или минимизация среднего времени доезда, используемая в задаче о p-медиане.
Цель моделей покрытия состоит в формировании некоторого набора покрывающих зон, которые могут быть обслужены машинами скорой помощи в пределах целевого временного интервала. В качестве ограничения классической модели покрытия Location Set Covering Model (LSCM) рассматривают расстояние или время, характерные для услуги. Все точки спроса, которые находятся в пределах порогового расстояния, считаются обслуженными (т.е. «покрытыми»). LSCM минимизирует количество объектов, необходимых для обслуживания всех точек спроса.
Модель Maximal Covering Location Problem (MCLP) максимизирует область покрытия, которую способны обслужить заданное количество объектов обслуживания. MCLP, получив на входе количество объектов обслуживания, решает задачу наилучшего их размещения для покрытия потребностей всех точек спроса. Аналогично LSCM модель MCLP строится из предположения, что точка спроса обслуживается, если хотя бы один объект обслуживания достигает ее за заданное время, либо, если расстояние между точкой спроса и объектом обслуживания не превышает заданный лимит.
В то время как модели покрытия ориентированы на то, чтобы обеспечить обслуживанием каждую точку спроса, не превысив определённый лимит времени, задача о p-медиане сфокусирована на минимизации общего или среднего времени доезда при условии обслуживания всех точек спроса.
Все указанные модели рассматриваются в основном как варианты для государственного сектора экономики, поскольку не учитывают затраты на размещение и функционирование объектов, однако многократные ссылки на них и частое использование в последующих исследованиях подчеркивает их важность для современной теории выбора месторасположения. Так, например, в работе [4] оптимизационная модель MCLP дополняется возможностями имитационного моделирования для обоснования решения о размещении пунктов скорой воздушной помощи.
Для решения оптимального местоположения отделений и станций СМП используются и методы интеллектуального анализа данных. Так, в статье Т.А. Дзюбы и И.Н. Розенберга применены методы нечеткой логики [5].
Продемонстрируем возможности кластерного анализа при решении проблемы оптимального местоположения станций скорой помощи, ориентированной на долгосрочный уровень планирования на примере г. Екатеринбурга.
Приведем математическую постановку задачи оптимального местоположения скорой медицинской помощи.
Пусть неориентированный граф G = (V, E) отображает улично-дорожную сеть города. Множество вершин V, заданных двумя координатами (широтой и долготой) задает множество зданий города. В контексте нашей работы будем считать, что вызовы в диспетчерскую службу поступают из вершин графа. Места расположения станций и отделений скорой помощи также соответствуют вершинам графа G.
Пусть заданы:
- граф улично-дорожной сети города G = (V, E);
- множество мест вызовов скорой помощи R;
- количество станций и отделений скорой помощи k.
Задача оптимального местоположения заключается в определении такого множества местоположений станций и отделений скорой помощи F, что
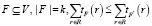 ,
,
для всех
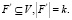
Здесь tF(r) – минимальное время доезда машины скорой помощи от места расположения машины у станции или отделения скорой помощи до места вызова r∈R.
Будем считать, что жизнь больного будет спасена, если машина скорой помощи, находясь в объекте обслуживания fj∈F, j = 1..k, прибудет к пациенту за минимально возможное время. Поскольку о местонахождении будущих пациентов заранее неизвестно, для достижения результата сведем к минимуму общее время доезда из станции скорой помощи fj = (xj, yj), обслуживающей район точек спроса, до каждой точки спроса района обслуживания ri = (pi, qi). Предполагая, что средняя скорость доезда постоянна, рассмотрим в качестве целевой функции эвклидово расстояние от места вызова r до станции скорой помощи. Пусть Rj – кластер пациентов, обслуживаемых станцией скорой помощи fj, тогда задача сводится к следующей:
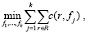 (1)
(1)
где
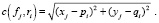 (2)
(2)
Для распределения множества точек спроса R по объектам обслуживания F будем использовать алгоритм кластеризации K-Medoid. Алгоритм был разработан С. Вассильвитским и Д. Артуром в 2007 г. [6] и представляет собой модификацию известного алгоритма кластеризации K-Means. Общей частью этих алгоритмов является пошаговый итеративный пересчет центров кластеров, длящийся до тех пор, пока идет улучшение качества результирующей кластеризации за счет замены центроидов. Но в отличие от K-Means в качестве нового центра кластера K-Medoid тестирует каждый объект исходного пространства данных. Итерации продолжаются до тех пор, пока центром – медоидом каждого кластера не станет наиболее близкий к центру кластера объект исходных данных.
В силу того, что алгоритм кластеризации K-Medoid использует в качестве центров кластеров реальные объекты исходного набора вершин, этот алгоритм является более предпочтительным для работы с объектами графов дорожной сети, чем алгоритм K-Means. С учетом достаточно плотной городской транспортной сети при использовании алгоритма кластеризации K-Medoid будем считать, что ограничения, налагаемые топологией дорог, несущественны и две вершины графа всегда связаны прямой дорогой, что позволит нам использовать евклидову метрику при расчете расстояний. В контексте нашего исследования можно сделать следующий вывод: для того, чтобы свести к минимуму время доезда каждой машины скорой помощи, до места вызова, станции и отделения скорой медицинской помощи необходимо разместить в местах расположения медоидов.
Опишем этапы проведенного вычислительного эксперимента.
Подготовка данных
Географические координаты зданий и объектов г. Екатеринбурга были взяты из Федеральной информационной адресной системы (ФИАС) – открытой базы данных всех адресов Российской Федерации Федеральной налоговой службы. Данные ФИАС представленные в формате XML, были импортированы в систему управления базами данных SQL Server. Была проведена очистка данных: выбраны необходимые для дальнейшей обработки поля, удалены все записи, не относящиеся к г. Екатеринбургу, а также все неактуальные записи. После чего были исключены записи об объектах, не являющихся улицами, бульварами, переулками и другими объектами того же уровня. В результате из 1,5 млн записей в таблице осталось 4,5 тысяч записей.
Полученная таблица была преобразована в список объектов, пригодный для обработки с помощью API Google Maps. При помощи программы, отправляющей запросы к Google Maps Geolocation API, были получены необходимые для исследования географические координаты объектов. Результатом работы является текстовый файл, каждая строка которого представляет собой пару координат каждого объекта требуемого уровня на карте Екатеринбурга.
Кластерный анализ полученных данных
В качестве инструментального средства выполнения кластерного анализа был использован пакет прикладных программ MATLAB от компании The Mathworks. Встроенный в MATLAB пакет Statistic Toolbox позволяет решать задачи кластерного анализа данных при помощи алгоритма K-Medoid, при этом генерируя исчерпывающую информацию о каждом кластере. Особенностью алгоритма K-Medoid является то, что он работает с заданным пользователем числом кластеров. Для определения количества кластеров использовали следующее соображение: площадь Екатеринбурга составляет 491 км2. Эмпирическим путем, исходя из 20-минутного целевого времени доезда, был выбран радиус области «покрытия» станцией скорой помощи в 50 км2. Таким образом, были рассмотрены следующие варианты количества кластеров: 9, 10 и 11.
После получения вариантов расчетов для 9, 10 и 11 кластеров, был проведен анализ полученных результатов и выбрано такое расположение возможных мест размещения станций и отделений скорой медицинской помощи, которое обеспечило бы минимальное время доезда от предлагаемого места расположения станции скорой медицинской помощи (центроида кластера) до самых удаленных точек района, прикрепленного к станции.
Выбор оптимальной модели
Выбор лучшей модели был проведен по следующему алгоритму.
Для каждой из трех моделей выбирался кластер с наиболее широким разбросом точек. Далее в этом кластере определялись три максимально удаленных от центроида кластера точки. С помощью Google Maps Distance Matrix API рассчитывалось время доезда от каждой выбранной точки до центроида. Было решено считать лучшей ту модель, когда суммарное время доезда от центроида (предполагаемого места расположения станции скорой медицинской помощи) до трех наиболее удаленных точек спроса было наименьшим.
Для кластеризации с 9 кластерами оценка общего времени доезда составила 48 мин, с 10 кластерами – 103 мин, для кластеризации с 11 кластерами – 100 мин. Таким образом, наиболее оптимальной оказалась модель с 9 кластерами.
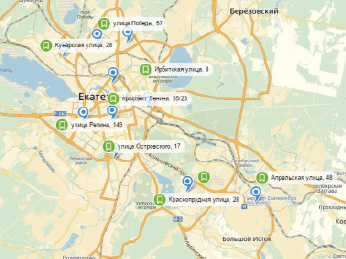
Карта существующих и предложенных мест размещения станций скорой медицинской помощи
Для отображения полученных результатов на рисунке на карту г. Екатеринбурга флажками нанесены действующие станции скорой медицинской помощи, запятые отмечают места предложенных по модели мест расположения станций и отделений.
Очевидно, что текущее расположение медицинских учреждений с функцией выездной помощи близко к оптимальному местоположению с точки зрения построенной модели. Однако тот же алгоритм оценки суммарного времени доезда для соответствующего реального района обслуживания показывает результат 97 мин, что на 9 мин превышает предложенный при моделировании результат.
Выводы
В настоящей работе мы предложили алгоритм расчета оптимального пространственного местоположения станций и отделений скорой медицинской помощи. Как недостаток можно отметить то, что предложенная модель не учитывает дороги и объекты, блокирующие проезд (закрытые территории, водные объекты и т.д.). Устранив этот недостаток, можно получить модель, более адекватно оценивающую реальную ситуацию. В последующих работах планируется при использовании аппарата кластерного анализа построить модели, которые обеспечат разумную загруженность станций скорой помощи и максимизируют выживаемость пациентов. Проверка эффективности моделей будет также проведена на данных г. Екатеринбурга.



