Проблема управления портфелем ценных бумаг является фундаментальной в финансовой теории и практике. Как задача управления в условиях высокой неопределенности – она относится также и к фундаментальной в теории принятия решений. Оперативное управление портфелем финансовых активов обусловливает широкое применение методов теории стохастических процессов и финансового моделирования.
В современных условиях оптимальное управление инвестиционным портфелем осложняется высокой волатильностью цен торгуемых активов и присутствием резких скачкообразных изменений, обусловленных экстернальными факторами, которые, как правило, невозможно предсказать на основании анализа исторических данных. Эти особенности динамики активов фондовых рынков существенно влияют на распределение доходности ценных бумаг, которое часто не совпадает с нормальным, а следовательно, сужаются перспективы использования «классической» теории портфеля Г. Марковица – Д. Тобина – У. Шарпа, основанные на чебышевском законе больших чисел [1–3].
Цель исследования: предложить методику определения приоритетной последовательности стратегий инвестирования для современного инвестора с применением синтетического критерия теории игр.
Материалы и методы исследования
Для проведения исследования нами были использованы открытые источники данных: интернет-ресурсы, анализирующие современные методы формирования инвестиционных стратегий, банки статистической информации, отчеты и нормативные документы Нью-Йоркской фондовой биржи, оригинальные труды основателей современной портфельной теории, а также научный труд Л. Лабскера, Н. Ященко, А. Амелиной – теоретическая база для предлагаемой методики. Путем синтеза доступной информации с ведущих торговых площадок, а именно результатов фундаментального анализа высоколиквидных ценных бумаг и прогнозов ведущих аналитиков, были отобраны финансовые инструменты и сформирован первоначальный набор портфелей. Далее, следуя предлагаемому алгоритму, в основе которого лежит практическое применение синтетического критерия теории игр Вальда – Сэвиджа, формируется приоритетная последовательность инвестиционных стратегий.
Результаты исследования и их обсуждение
Напомним, что модель финансового портфеля, предложенная Г. Марковицем, основывалась на дилемме «риск – доходность»: мерой изменения доходности ценных бумаг в портфеле была предложена дисперсия доходности, рассчитываемая с учетом ковариаций и стандартных отклонений доходности каждой пары и отдельных финансовых активов. Трансакционные издержки и налоги в модели предложено не учитывать с целью упрощения [1]. Портфель ценных бумаг независимо от индивидуальных предпочтений инвестора может быть составлен из нескольких активов, в совокупности максимизирующих доходность при заданном уровне риска. Также с учетом желаемого уровня доходности можно составить портфель с минимально возможным риском. Все существующие комбинации активов могут быть изображены на графике: «риск-ожидаемая доходность», ограничивающим желательные для инвестора портфели под некоторой кривой – эффективной границей. В реальных условиях на фондовых площадках, удовлетворяющих базовым условиям модели Г. Марковица, портфели вдоль эффективной границы ищутся без особых затруднений.
Для иллюстрации текущей вовлеченности стран в операции на фондовом рынке приведем данные Всемирного Банка, касающиеся отношения капитализации фондового рынка стран к ВВП за 2017 г. (данные по странам, для которых это значение превышает 40 %) (рисунок). Этот показатель стал значимым в финансовом анализе после высказывания У. Баффета о том, что он – лучший для вывода о переоцененности или недооценке рынка в целом [4]. Значение выше 100 % свидетельствует о первом явлении, а значение около 50 % свидетельствует о втором. Таким образом, условие эффективности рынка выполняется не для всех стран [5, с. 302–305].
Для развивающихся фондовых рынков, в особенности для которых характерны низкая ликвидность, не обеспечивающая защиту операции, неэффективность рынка и др. проблемы, возможности формирования эффективных портфелей могут быть рассмотрены только с учетом модификации подхода к формированию портфеля Г. Марковица и совершенствования алгоритмов портфельной теории и практики.
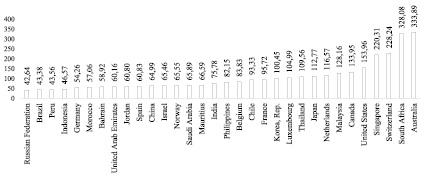
Отношение капитализации фондового рынка страны к ее ВВП в 2017 г. [6]
В связи с этим актуальной является проблематика совершенствования инструментария моделей и методов формирования и управления финансовыми портфелями как профессиональных игроков, так и непрофессиональных (так называемые неинституциональные инвесторы) агентов фондового рынка.
С учетом вновь возникающих потребностей инвесторов и «движений» рынка можно дополнять классическую модель Г. Марковица. Однако такой путь не может быть эффективным, так как изменение инструментария предполагает тщательную проработку, теоретические обоснования модификаций и последующее тестирование модели на рынках, отличных как условиями функционирования, так и параметрами торгуемых активов. Нами выбран другой путь, а именно формирование финансового портфеля с учетом предпочтений инвесторов, которые можно назвать в данном случае «дополнительными».
Продемонстрируем возможности этого подхода в приложении к задаче формирования среднесрочного инвестиционного портфеля умеренно агрессивного инвестора с невысоким инвестиционным бюджетом. К их числу отнесем неинституциональных инвесторов, целью которых является сохранение денежных средств в условиях инфляции. Ожидания доходности инвестиции в рассматриваемые портфели не выше средней по рынку, однако требования к надежности финансовых инструментов в портфеле более жесткие: инвестор толерантен к риску, но его величина выше априорно заданного уровня недопустима. Также, для своевременного выхода из сделки необходимо, чтобы инструменты характеризовались соответствующим уровнем ликвидности. Данная группа инвесторов ориентируется на среднесрочный горизонт инвестирования (от 6 месяцев до 2 лет [7, с. 38–39]).
Предлагается рассмотреть перспективы использования в задаче выбора оптимального портфеля для инвесторов рассматриваемой группы синтетического критерия Вальда – Сэвиджа, предложенного Л. Лабскером. Выбор инструментария моделей «игр с природой» обусловлен присущей фондовому рынку неопределенностью, порождаемой нестабильной макроэкономической ситуацией, изменчивой рыночной конъюнктурой, ожиданиями участников рынка и другими факторами, оказывающими непосредственное влияние на котировки ценных бумаг.
Синтетический критерий Вальда – Сэвиджа позволяет оценить оптимальность рассматриваемых субъектом-агентом рыночного взаимодействия (в нашем случае – неинституционального инвестора) стратегий поведения с позиции и выигрыша, и риска. Он представляет собой линейную комбинацию критериев Вальда и Сэвиджа с коэффициентами, определяющими количественную оценку степеней предпочтения субъекта к выигрышам и риску [8, с. 19].
Для неинституционального инвестора предлагается построить вариант традиционной модели Г. Марковица, по результатам реализации которой на «выходе» планируется получить не менее m альтернативных портфелей финансовых инструментов, однородных по ликвидности, срокам инвестирования, величине инвестиционного бюджета и отличающихся по доходности и риску.
Ниже приведем краткое описание модели Г. Марковица формирования оптимального портфеля для рассматриваемого неинституционального инвестора, на основании которой будет базироваться решение поставленной задачи, а также введем формальное определение синтетического критерия Вальда – Сэвиджа.
Оптимизационная модель портфеля, составленного из n ценных бумаг, выглядит следующим образом:
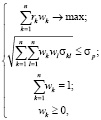 (1)
(1)
где k, l – индексы активов; rk – средняя ожидаемая доходность k-го актива инвестиционного портфеля; σkl – ковариация доходностей k-го и l-го актива в портфеле ценных бумаг; σp – приемлемый для инвестора уровень риска; wk – доля k-го финансового актива в инвестиционном портфеле [1].
Синтетический критерий Вальда – Сэвиджа включает:
– критерий Вальда, позволяющий определить оптимальность стратегии с позиции выигрыша;
– критерий Сэвиджа, дающий возможность выбрать стратегию с позиции игрового риска.
Оптимальной во множестве чистых стратегий по критерию Вальда или W-оптимальной является стратегия, обеспечивающая W-максимальный среди минимальных выигрышей в чистых стратегиях. Выбранное таким образом оптимальное решение исключает риск, и в каком бы состоянии ни находилась «природа», полученный результат не может быть ниже W. Данный критерий в литературе называется «принципом гарантированного результата» и определяется как критерий «крайнего пессимизма относительно выигрышей» [8, с. 115–117], применяемый в случаях, когда целью субъекта является не выигрыш, а нежелание проиграть, что в точности соответствует формализации предпочтений рассматриваемой группы неинституциональных инвесторов.
Оптимальной во множестве чистых стратегий по критерию Сэвиджа или S-оптимальной является стратегия, обеспечивающая минимальный среди максимальных рисков в чистых стратегий – S. В литературе данный критерий также определяют как «критерий крайнего пессимизма», так как при выборе стратегии субъект ориентируется на наибольший риск, а именно на то, что «природа» будет находиться в наихудшем для игрока состоянии [8, с. 125–126].
Их линейная комбинация, как упоминалось выше, позволит подойти к выбору оптимальной с позиции выигрыша и риска стратегии инвестора.
Введем для формального описания синтетического критерия коэффициенты, характеризующие степень предпочтения инвестором выигрыша и риска: r∈[0,1] и (1 – r). Выбор численного значения показателя r является субъективным, зависит от требуемой ожидаемой доходности и толерантности к риску [8, с. 138].
Критерий Вальда – Сэвиджа с выигрыш-показателем r∈[0,1] определим следующим образом:
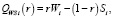 (2)
(2)
где Wi – показатель эффективности стратегии Ai по критерию Вальда; Si – показатель эффективности стратегии Ai по критерию Сэвиджа, i∈I.
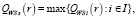 (3)
(3)
где QWs(r) – цена игры в чистых стратегиях.
Назовем оптимальной стратегию Af на множестве s чистых стратегий при условии, что
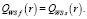 (4)
(4)
Множество QWS(r)-оптимальных на множестве s чистых стратегий обозначим как 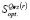 .
.
В цитируемой работе доказано, что каждая стратегия, являющаяся оптимальной на множестве s чистых стратегий по критерию Вальда – Сэвиджа, является оптимальной на множестве s как по критерию Вальда, так и по критерию Сэвиджа. Также, при r∈(0,1) структура множества 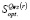 стратегий, оптимальных на множестве чистых стратегий по критерию Вальда – Сэвиджа с выигрыш-коэффициентом r, не зависит от значений r∈(0,1) [8, с. 147–155].
стратегий, оптимальных на множестве чистых стратегий по критерию Вальда – Сэвиджа с выигрыш-коэффициентом r, не зависит от значений r∈(0,1) [8, с. 147–155].
Для практического использования описанной выше модели предлагаем воспользоваться следующим алгоритмом, первоначально предложенным Л. Лабскером и усовершенствованным для целей настоящей работы.
Предварительно считаем необходимым ввести следующие допущения: неинституциональный инвестор выбирает стратегию вложения средств из полученной в результате расчетов ранжированной очереди не менее чем m портфелей ценных бумаг; ограничения на риск задаются извне; ограничения на ликвидность финансовых инструментов не вводятся, так как предполагается, что портфели формируются на фондовых рынках из активов с высокой ликвидностью.
Алгоритм:
1. Сформировать инвестиционные портфели по традиционной модели Г. Марковица для отобранных финансовых инструментов, определить их характеристики.
Для использования синтетического критерия Вальда – Сэвиджа необходимо выделить показатель для сравнительной оценки портфелей. В этом качестве предлагается использовать коэффициент Шарпа, который рассчитывается по следующей формуле:
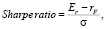 (5)
(5)
где Er – ожидаемая доходность портфеля, rF – безрисковая доходность, σ – стандартное отклонение портфеля [9, с. 84–85]. Он позволяет оценить «выигрыш», который инвестор может получить от вложения в рассматриваемые портфели, скорректированный на рисковую составляющую. Коэффициент Шарпа, рассчитанный для сформированных портфелей, необходимо сравнить с рассчитанным для рыночного индекса. Сравнение позволит оценить, лежит ли полученный портфель выше или ниже линии рынка капитала
2. Сформировать матрицу A выигрышей, элементами которой будут коэффициенты Шарпа составленных портфелей за рассматриваемые периоды;
3. Используя формулу
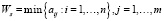 , (6)
, (6)
найти показатели эффективности Wi, i∈I, стратегий Ai, i∈I, по критерию Вальда, цену игры Ws в чистых стратегиях по критерию Вальда.
4. Определить множество стратегий, оптимальных во множестве чистых стратегий по критерию Вальда: 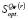 .
.
5. По данным матрицы А составить матрицу рисков R.
6. По данным матрицы R рассчитать показатели Si, определить цену игры по критерию Сэвиджа в чистых стратегиях, Ss по формуле:
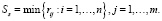 (7)
(7)
7. Определить множество стратегий, оптимальных во множестве чистых стратегий по критерию Сэвиджа: 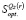 .
.
8. По данным пунктов 4 и 7 проверить выполнимость условия
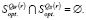
Если оно не выполняется, то множество стратегий 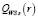 -оптимальных на множестве s имеет структуру:
-оптимальных на множестве s имеет структуру:
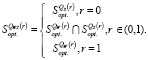 (8)
(8)
В противном случае – переходим к следующему пункту.
9. По данным пунктов 4 и 6 определить цену игры 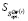 в стратегиях множества
в стратегиях множества 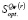 по критерию Сэвиджа.
по критерию Сэвиджа.
10. По данным пунктов 3 и 7 рассчитать цену игры 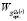 в стратегиях множества
в стратегиях множества 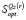 по критерию Вальда.
по критерию Вальда.
11. По данным пунктов 4 и 7 определить множество стратегий, не являющихся оптимальными на множестве чистых стратегий ни по критерию Вальда, ни по критерию Сэвиджа.
12. Для каждой стратегии, определенной в пункте 11, с использованием пунктов 3, 6, 9, 10 проверить справедливость неравенства:
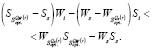 (9)
(9)
Если для хотя бы одной стратегии данное неравенство не выполняется, то расчеты завершаются, и о структуре 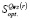 нельзя сказать ничего определенного. Если неравенство выполняется, переходим к следующему пункту.
нельзя сказать ничего определенного. Если неравенство выполняется, переходим к следующему пункту.
13. По данным пунктов 3 и 7 определить множество 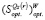 , оптимальных на
, оптимальных на 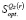 по критерию Вальда.
по критерию Вальда.
14. По данным пунктов 4 и 6 определить множество 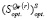 , оптимальных на
, оптимальных на 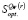 по критерию Сэвиджа.
по критерию Сэвиджа.
15. По данным пунктов 3, 6, 9, 10 рассчитать значение 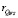 по формуле
по формуле
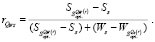 (10)
(10)
16. По данным пунктов 4, 7, 13, 14, 15 определить структуру множества оптимальных чистых стратегий 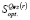 по формуле
по формуле
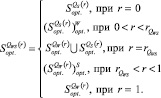 (11)
(11)
Рассмотрим следующий пример.
Задана игра с природой и для нее сформирована матрица выигрышей:
|
Пj Аi |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
Wi |
|
|
А1 |
0,0953 |
0,2681 |
0,1750 |
–0,2681 |
0,0729 |
–0,0807 |
–0,2681 |
|
|
А2 |
0,0221 |
0,2213 |
0,1871 |
–0,2631 |
0,0612 |
–0,1127 |
–0,2631 |
|
|
А3 |
0,0217 |
0,2205 |
0,1866 |
–0,2630 |
0,0611 |
–0,1135 |
–0,2630 |
(11.1) |
|
А4 |
0,4458 |
0,0611 |
–0,1195 |
–0,2393 |
0,0832 |
–0,2587 |
–0,2587 |
|
|
А5 |
0,0451 |
0,2366 |
0,1886 |
–0,2658 |
0,0643 |
–0,1057 |
–0,2658 |
|
|
А6 |
0,1583 |
0,1243 |
0,2144 |
–0,2184 |
0,0742 |
–0,0702 |
–0,2184 |
|
|
βj |
0,4458 |
0,2681 |
0,2144 |
–0,2184 |
0,0832 |
–0,0702 |
Ws = –0,2184 |
В последнем столбце матрицы выигрышей рассчитаны показатели эффективности Wi, i = 1,2,…,6 стратегий Аi, i = 1,2,…,6, по критерию Вальда. В последней строке – показатели благоприятности βj, i = 1,2,…,6, состояний природы Пj, i = 1,2,…,6. Определим структуру множества 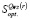 cтратегий, оптимальных во множестве чистых стратегий по синтетическому критерию Вальда – Сэвиджа по описанному алгоритму.
cтратегий, оптимальных во множестве чистых стратегий по синтетическому критерию Вальда – Сэвиджа по описанному алгоритму.
В используемой интерпретации матрица выигрышей сформирована из коэффициентов Шарпа для шести портфелей и для различных «состояний природы» (под последним подразумеваются периоды, для которых эти коэффициенты были рассчитаны).
Показатели эффективности стратегий по критерию Вальда найдены и представлены в последнем столбце матрицы (11.1). Цена игры в чистых стратегиях по критерию Вальда: Ws = –0,2184.
Из последнего столбца следует, что W6 = Ws = –0,2184. Поэтому стратегия А6 оптимальна по критерию Вальда, следовательно, 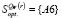 .
.
Составим матрицу рисков, порождаемую матрицей выигрышей (11.1):
|
Пj Аi |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
Si |
|
|
А1 |
0,3505 |
0,0000 |
0,0394 |
0,0497 |
0,0103 |
0,0105 |
0,3505 |
|
|
А2 |
0,4237 |
0,0468 |
0,0273 |
0,0447 |
0,0220 |
0,0426 |
0,4237 |
(11.2) |
|
А3 |
0,4241 |
0,0476 |
0,0278 |
0,0446 |
0,0221 |
0,0434 |
0,4241 |
|
|
А4 |
0,0000 |
0,2070 |
0,3339 |
0,0209 |
0,0000 |
0,1886 |
0,3339 |
|
|
А5 |
0,4007 |
0,0315 |
0,0258 |
0,0474 |
0,0189 |
0,0355 |
0,4007 |
|
|
А6 |
0,2875 |
0,1439 |
0,0000 |
0,0000 |
0,0090 |
0,0000 |
0,2875 |
Показатели рассчитаны и представлены в последнем столбце матрицы (11.2). Цена игры по критерию Сэвиджа Ss = 0,2875. Множество стратегий 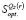 , оптимальных во множестве чистых стратегий по критерию Сэвиджа, состоит из одной стратегии А6, следовательно,
, оптимальных во множестве чистых стратегий по критерию Сэвиджа, состоит из одной стратегии А6, следовательно, 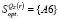 .
.
Используя (11.1) и (11.2), найдем по формуле (2) значение критерия для каждой стратегии, в концах отрезка [0,1] и представим в табл. 1.
Таблица 1
Показатель эффективности на концах отрезка [0,1]
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
QWSi(0) |
–0,3505 |
–0,4237 |
–0,4241 |
–0,3339 |
–0,4007 |
–0,2875 |
|
QWSi(1) |
–0,2681 |
–0,2631 |
–0,2630 |
–0,2587 |
–0,2658 |
–0,2184 |
Из полученных результатов расчетов видно: левый конец 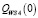 отрезка
отрезка 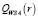 стратегии А4 меньше показателя в левом конце стратегии А6; правый конец
стратегии А4 меньше показателя в левом конце стратегии А6; правый конец 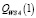 стратегии А4 больше правых концов стратегий А1, А2, А3, А5. Таким образом, установлены взаимные пересечения отрезков
стратегии А4 больше правых концов стратегий А1, А2, А3, А5. Таким образом, установлены взаимные пересечения отрезков 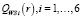 , которые представим в табл. 2.
, которые представим в табл. 2.
Пометка «х» в ячейках означает пересечение отрезков. Далее найдем значения r на пересечении каждого отрезка, решая уравнение 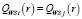 . Получим следующие значения r для каждого пересечения: r12 = 0,9350; r23 = 0,9738; r15 = 0,9552; r25 = 0,8939; r35 = 0,8950.
. Получим следующие значения r для каждого пересечения: r12 = 0,9350; r23 = 0,9738; r15 = 0,9552; r25 = 0,8939; r35 = 0,8950.
Таблица 2
Пересечения отрезков 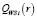
|
№ отрезка i, j |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
x |
x |
||||
|
2 |
x |
x |
x |
|||
|
3 |
x |
x |
||||
|
4 |
||||||
|
5 |
x |
x |
x |
|||
|
6 |
Значения показателя эффективности 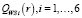 при значениях r = 0, r12, r23, r15, r25, r35, 1 и номера стратегий в последовательности при полученных r представим в табл. 3.
при значениях r = 0, r12, r23, r15, r25, r35, 1 и номера стратегий в последовательности при полученных r представим в табл. 3.
Итак, рассчитаны показатели эффективности для каждой из стратегий. Далее они проранжированы в невозрастающем порядке и каждому полученному значению присвоен порядковый номер (в таблице номера проставлены под полученными показателями эффективности). Если номера нескольких расчетных показателей эффективности в одной строке совпадают, то для соответствующих стратегий номера в приоритетной последовательности могут меняться. Если ищется номер чистой стратегии в приоритетной последовательности для r, находящемся в интервале, то стратегии будет присвоен номер места в приоритетной последовательности, общий для концов этого интервала. Например, для стратегии А1 общим порядковым номером места в приоритетной последовательности является номер 6 при значении выигрыш-показателя на концах интервала (0,9738;1). Следовательно, при любом значении r из данного интервала стратегия А1 займет 6 место.
Таблица 3
Определение приоритетной последовательности инвестиционных портфелей по критерию Вальда – Сэвиджа
|
Значение показателя r |
Показатели эффективности |
|||||
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
|
|
0 |
–0,35048 |
–0,42373 |
–0,42408 |
–0,33390 |
–0,40072 |
–0,28753 |
|
3 |
5 |
6 |
2 |
4 |
1 |
|
|
0 < r < 0,8939 |
3 |
5 |
6 |
2 |
4 |
1 |
|
0,8939 |
–0,27688 |
–0,28010 |
–0,28013 |
–0,26671 |
–0,28010 |
–0,22574 |
|
3 |
4 |
6 |
2 |
4 |
1 |
|
|
0,8939 < r < 0,8950 |
3 |
4 |
6 |
2 |
4 |
1 |
|
0,8950 |
–0,27679 |
–0,27993 |
–0,27996 |
–0,26663 |
–0,27996 |
–0,22566 |
|
3 |
4 |
5 |
2 |
5 |
1 |
|
|
0,8950 < r < 0,9350 |
3 |
4 |
5 |
2 |
5 |
1 |
|
0,9350 |
–0,27350 |
–0,27350 |
–0,27351 |
–0,26363 |
–0,27455 |
–0,22290 |
|
3 |
3 |
5 |
2 |
6 |
1 |
|
|
0,9350 < r < 0,9552 |
3 |
3 |
5 |
2 |
6 |
1 |
|
0,9552 |
–0,27184 |
–0,27026 |
–0,27027 |
–0,26211 |
–0,27184 |
–0,22151 |
|
5 |
3 |
4 |
2 |
5 |
1 |
|
|
0,9552 < r < 0,9738 |
5 |
3 |
4 |
2 |
5 |
1 |
|
0,9738 |
–0,27031 |
–0,26728 |
–0,26728 |
–0,26072 |
–0,26933 |
–0,22022 |
|
6 |
3 |
3 |
2 |
5 |
1 |
|
|
0,9738 < r < 1 |
6 |
3 |
3 |
2 |
5 |
1 |
|
1 |
–0,26815 |
–0,26306 |
–0,26305 |
–0,25874 |
–0,26579 |
–0,21841 |
|
6 |
4 |
3 |
2 |
5 |
1 |
|
Полученные последовательности позволяют сформулировать рекомендации для неинституционального инвестора. Так, выбирая наименее рискованный вариант, сформирована следующая приоритетная последовательность выбора стратегий: А6, А4, А1, А5, А2, А3.
Заключение
Проделанная работа позволяет сделать вывод о том, что формирование надежной инвестиционной стратегии – сложный процесс, требующий комплексного анализа доступной информации о динамике фондовых рынков. Однако в текущих условиях, когда каждому инвестору требуется более «индивидуальный» подход, предлагаемый алгоритм может стать решением этой непростой задачи.
Таким образом, из полученных результатов расчетов инвестор в зависимости от готовности рисковать способен определить для себя приоритетную последовательность стратегий инвестирования.




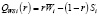 чистых стратегий Ai
чистых стратегий Ai