Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Байесовский подход нашёл широкое применение при оценивании эконометрических моделей по выборочным данным малого объема, а также в случаях, когда классические методы неприменимы. В рамках классического подхода, для оценки некоторого вектора параметров модели θ по выборочным данным Y, например, методом максимального правдоподобия (ММП), выбирается целевая функция – функция правдоподобия, и находится такая оценка

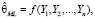(1)

которая её максимизирует

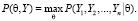(2)

Вектор параметров θ – неслучаен, а ММП-оценка (1), вычисляемая по выборочным данным – случайна. Байесовский метод – это способ формализации степени разумной уверенности в некотором утверждении, и ее корректировки по мере поступления информации относительно исследуемого явления. Поэтому в байесовском подходе оцениваемый вектор параметров θ трактуется как случайный с заданным в явном виде априорным распределением P(θ). Выбор априорного распределения отражает степень незнания исследователя о неизвестных параметрах до проведения и обработки наблюдений, и задача байесовского оценивания заключается в поиске апостериорного распределения, скорректированного по результатам наблюдений:

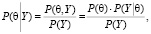(3)

где P(θ) – плотность априорного распределения, 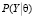– функция правдоподобия. Поскольку P(Y) выполняет роль нормирующего множителя, и не зависит от вектора параметров, то (3) можно записать в виде

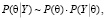(4)

где символ ~ означает пропорциональность левой и правой частей выражения (4) с точностью до нормирующей константы. Имея выборочные данные и вычислив функцию правдоподобия, можно найти условный закон распределения при данной выборке, по которому рассчитать точечные и интервальные оценки эконометрической модели.

Цель исследования: сравнительный анализ оценок параметров эконометрической модели в рамках байесовской регрессии и метода максимального правдоподобия. В качестве инструментальных средств выбрана программная среда R, в которой байесовская парадигма представлена в функциях многих статистических пакетов. Результаты, приведенные в статье, получены при помощи пакета MCMC (Monte Carlo Markov chain), основу которого составляет построение марковского процесса, стационарное распределение которого определяется апостериорной функцией распределения [1, 2].

Результаты исследования и их обсуждение

Алгоритм байесовского оценивания имеет следующую последовательность [3]:

1) выбор априорного распределения P(θ) параметра θ;

2) сбор статистических данных: Y1, Y2,..., Yn (случайная выборка из анализируемой генеральной совокупности);

3) вычисление функции правдоподобия, в предположении статистической независимости наблюдений:

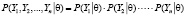; (5)

4) вычисление апостериорного распределения параметра θ: 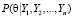по формуле (4);

5) заключение о значении параметра θ: точечная или интервальная оценка.

Под байесовской точечной оценкой параметра понимается математическое ожидание или мода случайной величины, имеющей апостериорное распределение (4), например, для непрерывного случая:

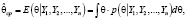(6)

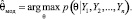(7)

Интервальные оценки параметров так же определяются через функцию апостериорного закона распределения вектора параметров (Highest Posterior Density, HPD – интервал высокой апостериорной плотности) [4].

При практической реализации байесовского подхода, в частности выбора априорного распределения, существенную роль играют распределения, сопряжённые с функцией правдоподобия. В этом случае общий вид априорного закона распределения известен, нужно только «уточнить» его параметры при переходе к апостериорному. Сопряженное семейство априорных распределений существует, если функцию правдоподобия можно представить в виде произведения достаточных статистик:

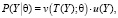(8)

где 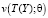– неотрицательная функция, зависящая от Y только через T(Y), u(Y) – положительная функция от выборочных данных, независящая от параметров [5].

В теории байесовского подхода доказывается, что если априорное распределение генеральной совокупности имеет функции сопряжённые с функцией распределения, то уже первый переход от априорного к апостериорному распределению по формуле (4) приводит к семейству распределений, сопряжённому с наблюдаемой генеральной совокупностью, даже если априорное распределение не несёт никакой информации об оцениваемых параметрах (САЗ – скудность априорных знаний [3], априорные распределения). Это позволяет упростить процедуру выбора априорного распределения для оцениваемого параметра:

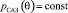(9)

– для параметра, принимающего значения на конечном 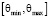или бесконечном 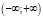интервалах;

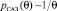(10)

– для параметра, принимающего любые положительные значения, и в качестве априорных распределений неизвестных параметров рекомендуется использовать равномерные распределения.

Выбор семейства априорных распределений, сопряженных с наблюдаемой генеральной совокупностью, осуществляется в результате следующих шагов:

1) выполняется проверка условия существования семейства априорных распределений (8), сопряженных с функцией правдоподобия для наблюдаемой генеральной совокупности;

2) выполняется вывод САЗ-апостериорного распределения, которое и определяет общий вид семейства априорных распределений, сопряженных с наблюдаемой генеральной совокупностью:

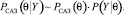(11)

Оценим параметры линейной регрессионной модели зависимости среднедушевых сбережений Y от доходов X у одинаковых по численному составу домохозяйств (по данным таблицы) в рамках ММП и байесовского подхода.

Выборочные данные переменных модели (в условных единицах) [6]

Спецификация оцениваемой модели 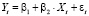, t = 1,..., n, или в матричном виде

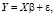(12)

где 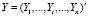– вектор-столбец значений эндогенной переменной, X – детерминированная (n×k)-матрица регрессоров, 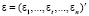– вектор-столбец возмущений, 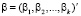– вектор-столбец параметров модели, n – объем выборки, k – число параметров, t – номер наблюдения, 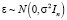, σ² – дисперсия случайного возмущения, 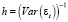– параметр точности (precision metrics), 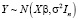– вектор эндогенной переменной, плотность (5) которого представляет собой априорную функцию распределения:

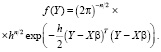(13)

ММП-оценки параметров при регрессорах совпадают с МНК-оценками, поэтому оценим их в программной среде R при помощи функции lm пакета lmtest:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.592462 1.088620 -2.381 0.032 *

X 0.118612 0.007747 15.310 3.88e-10 ***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.406 on 14 degrees of freedom

Multiple R-squared: 0.9436, Adjusted R-squared: 0.9396

F-statistic: 234.4 on 1 and 14 DF, p-value: 3.88e-10

confint(fm,level=0.90)

# интервальная оценка параметров

5 % 95 %

(Intercept) -4.5098597 -0.6750641

X 0.1049671 0.1322574

# автоковариационная матрица вектора оценок параметров

(Intercept) X

(Intercept) 1.185093948 -7.029648e-03

X -0.007029648 6.001834e-05

Для оценки параметров в рамках байесовского подхода необходимо проверить выполнение условия (8) существования семейства сопряженного априорного распределения p(β; h). Достаточной статистикой функции (13) является функции T(Y, X), которая определяется произведениями Y'Y, X'Y, X'X, что означает, что существует априорное распределение неизвестных параметров β и σ², сопряжённое с функцией правдоподобия. Преобразуем отклонение Y – Xβ в формуле (13) следующим образом:

,

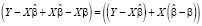тогда аргумент функции 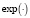принимает вид

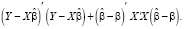(14)

Выражая первое слагаемое в (14) через несмещенную оценку дисперсии возмущений, 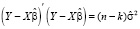, и подставляя (14) в (13), получим

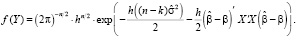(15)

Определим САЗ-апостериорное распределение для параметров модели множественной регрессии. Так как параметр точности h принимает положительные значения, то (11), с учетом правила (10) и формулы (15), принимает вид

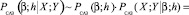
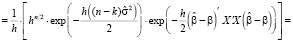
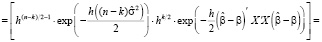
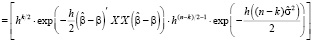. (16)

Перепишем (16) вводя обозначения: , ,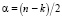

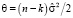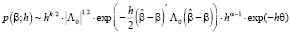. (17)

Распределение (17) представляет собой (с точностью нормирующего множителя, независящего от параметров) многомерное гамма-нормальное распределение с параметром сдвига 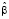, матрицей точности X'X и параметрами α и θ.

При реализации байесовского подхода необходимо знать параметры сопряженного с наблюдаемой генеральной совокупностью априорного распределения. В большинстве случаев они определяются при помощи метода моментов по оценкам их математического ожидания и среднеквадратическим ошибкам. Для этой цели обычно используется любая априорная информация, например экспертное оценивание. Воспользуемся ММП-оцениванием. Так как частное распределение параметра точности h нормальной части распределения (17) имеет гамма-распределение с параметрами α и θ, его числовые характеристики определяются по формулам

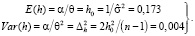(18)

Выражая из (18) параметры распределения через числовые характеристики параметра точности, получаем

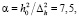
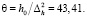(19)

Частное распределение параметра β есть обобщённое (k + 1)-мерное распределение Стьюдента с 2α числом степеней свободы, параметром сдвига β и матрицей точности 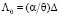, поэтому его числовые характеристики определяются по формулам

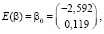
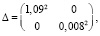
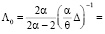
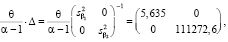(20)

где 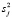– заданные значения априорных дисперсий элементов вектора параметров β.

По параметрам априорного распределения (19) и (20), выборочным данным (Y, X), вычисляются точечные оценки параметров апостериорного распределения (17):

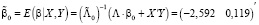, (21)

где

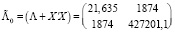(22)

– матрица точности; и параметры частного апостериорного гамма-распределения параметра точности h:

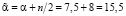, (23)

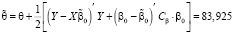, (24)

параметр точности:

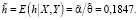(25)

При построении интервальных оценок, в рамках байесовского подхода, используется блочная структура матрицы точности:

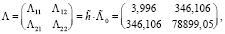
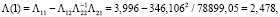
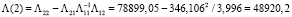(26)

и интервальные оценки параметров модели определяются по формулам:

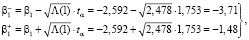(27)

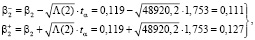(28)

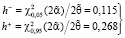, (29)

с учетом t0,05(2•7,5) = 1,753, , .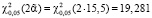

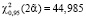Получим точечные и интервальные оценки параметров регрессионной модели зависимости среднедушевых сбережений Y от доходов X, по данным таблицы, при помощи функции MCMCregress пакета MCMCpack:

Iterations = 1001:11000

Thinning interval = 1

Number of chains = 1

Sample size per chain = 10000

1. Empirical mean and standard deviation for each variable,

plus standard error of the mean:

Mean SD Naive SE Time-series SE

(Intercept) -2.5893 0.263544 2.635e-03 2.602e-03

X 0.1186 0.001891 1.891e-05 1.891e-05

sigma2 5.8883 2.491154 2.491e-02 2.491e-02

2. Quantiles for each variable:

2.5 % 25 % 50 % 75 % 97.5 %

(Intercept) -3.1076 -2.7657 -2.5873 -2.4127 -2.0698

X 0.1148 0.1173 0.1186 0.1199 0.1224

sigma2 2.8866 4.2309 5.3662 6.9210 12.0544

Заключение

Как следует из сравнительного анализа результатов оценивания, интервальные оценки параметров регрессионной модели, полученные в рамках байесовского подхода, при непосредственном вычислении по формулам (18)–(29) уже, по сравнению с ММП-оценками: для параметра β1 – в 1,72 раза, для параметра β2 – в 1,75 раз, и при вычислении при помощи функции MCMCregress в программной среде R – для параметра β1 – в 3,7 раза, для параметра β2 – в 4 раза.