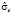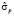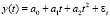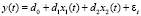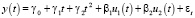В работе рассматривается задача прогнозирования эндогенной переменной по многомерным временным рядам экзогенных переменных. Построение регрессионной модели затрудняется наличием мультиколлинеарности экзогенных переменных, если у них есть временной тренд. В этом случае дисперсии коэффициентов регрессии становятся большими и, соответственно, оценки коэффициентов неточны. В настоящей работе предложена модификация трендово-факторной модели, описанной в [1], свободная от высокой коррелированности определяющих переменных xj(t) и в то же время позволяющая получить оценки коэффициентов регрессии по исходным переменным с меньшей дисперсией. Также дана количественная оценка повышения точности прогноза, показано, что ошибка модифицированной трендово-факторной модели меньше ошибок трендовой модели (модель 1) и регрессионной модели y(t) по исходным временным рядам xj(t) (модель 2).
Прогнозирование эндогенной переменной y(t) по значениям экзогенных переменных, представляющих собой временные ряды x1(t), x2(t),…xm(t), зачастую не может осуществляться с помощью классической линейной модели регрессии. Это связано с тем, что переменные xj(t) (j = 1,…,m) обычно имеют тренд fj(t), и, даже если xj(t) и xk(t) логически не связаны между собой, между ними возникает значительная корреляция (ложная корреляция), а большие значения коэффициента корреляции свидетельствуют о наличии мультиколлинеарности экзогенных переменных, что приводит к большим дисперсиям коэффициентов регрессии. В то же время можно, учтя причину ложной корреляции и несколько изменив спецификацию модели регрессии, получить модель линейной регрессии, пригодную для прогнозирования [2]. Уменьшения ошибки прогноза по сравнению с трендовой моделью или моделью регрессии y(t) по временным рядам xj(t) можно добиться, если рассматривать трендово-факторную регрессионную модель зависимости y(t) от t и отклонений определяющих переменных xj(t) от своих трендов. Оценка тренда в модифицированной таким образом трендово-факторной модели отличается от оценки тренда в трендовой модели, поскольку она строится не только с учётом зависимости y(t) от времени t, но и с учётом влияния на эндогенную переменную y(t) регрессоров xj(t).
Материалы и методы исследования
В настоящей работе были исследованы зависимости агрегата денежной массы Y (млрд долл.) от ВНП X1 (млрд долл.) и процентной ставки по 6-месячным государственным облигациям США X2 ( %) за 25 лет с помощью модифицированной трендово-факторной модели.
Результаты исследования и их обсуждение
1. Без ограничения общности, рассмотрим случай, когда тренды регрессоров xj(t) (j = 1,…,m) являются полиномами не выше второй степени. Значения j-й переменной в момент времени t имеют вид
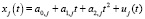 . (1)
. (1)
При этом будем считать, что оценки коэффициентов ak,j получены с помощью метода наименьших квадратов (МНК) и, следовательно, 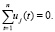 Спецификация классической линейной модели регрессии y(t) на xj(t) (j = 1,…,m) имеет вид
Спецификация классической линейной модели регрессии y(t) на xj(t) (j = 1,…,m) имеет вид
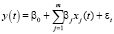 , t = 1,2,…,n. (2)
, t = 1,2,…,n. (2)
Подставляя (1) в (2), получаем
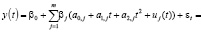
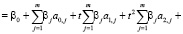
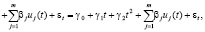
где через γ0, γ1, γ2 обозначены суммарные коэффициенты при t0, t и t2, соответственно. В результате получили следующую специ- фикацию регрессионной модели:
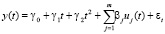 , (3)
, (3)
где 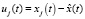 – отклонения xj(t) от тренда
– отклонения xj(t) от тренда 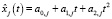 , (j = 1,…,m). Отметим, что если y(t) имеет линейный тренд, а хоть один из xj(t) имеет параболический тренд, то в модифицированной трендово-факторной модели (3) должен присутствовать член γ2t2. Заметим также, что коэффициенты регрессии βj в (3) те же самые, что и коэффициенты регрессии y(t) на xj(t) (j = 1,…,m) в (2).
, (j = 1,…,m). Отметим, что если y(t) имеет линейный тренд, а хоть один из xj(t) имеет параболический тренд, то в модифицированной трендово-факторной модели (3) должен присутствовать член γ2t2. Заметим также, что коэффициенты регрессии βj в (3) те же самые, что и коэффициенты регрессии y(t) на xj(t) (j = 1,…,m) в (2).
Коэффициенты регрессии γl и βj будем оценивать с помощью МНК. Для прогнозирования y(t) по модели (3) надо иметь прогнозные значения uj(t). В практических исследованиях вектор прогнозных значений u(L), как правило, неизвестен, однако, так как среднее остатков uj(t) (t = 1,…,n) равно нулю при оценивании с помощью МНК, то логично положить прогнозные значения uj(L) равными нулю. Тогда прогнозирование будет осуществляться по формуле
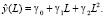 (4)
(4)
Параметры тренда в (4) отличаются от параметров, полученных по трендовой модели y(t), поскольку в (3) присутствуют ещё регрессоры uj(t). По этой же причине доверительные интервалы прогнозов по (4) будут меньше соответствующих интервалов при прогнозировании по трендовой модели, в которой учитывается только время t и не учитывается влияние других факторов. Ниже будет дана количественная оценка повышения точности прогноза.
2. Пусть U – матрица значений регрессоров модели (3), T – левая часть матрицы U, D – правая часть матрицы U,
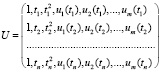 ,
, 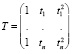 ,
,
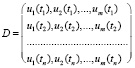 ,
, 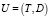 .
.
Стандартная ошибка прогноза 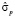 при t = L равна [3]
при t = L равна [3]
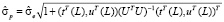 , (5)
, (5)
где 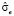 – стандартная ошибка модели (3), знак Т означает транспонирование,
– стандартная ошибка модели (3), знак Т означает транспонирование,
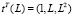 ,
, 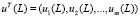 .
.
Запишем U в виде блочной матрицы U = (T, D).
Тогда матрица 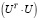 примет вид
примет вид 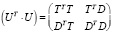 .
.
Обратная матрица 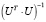 равна [4]
равна [4] 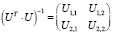 , где
, где
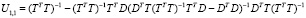 ,
,
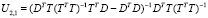 ,
,
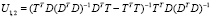 ,
,
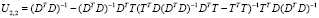 .
.
Обозначим: 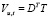 ;
; 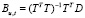 ;
; 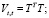
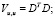
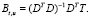
Тогда матрица 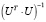 примет вид
примет вид
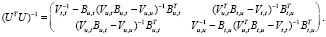
Пусть 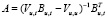 . Так как матрица
. Так как матрица 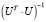 симметрична, то
симметрична, то 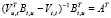 . Тогда матрицу
. Тогда матрицу 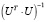 можно записать в виде
можно записать в виде
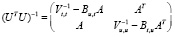 . (6)
. (6)
В матрице D записаны uj(ti) – остатки регрессии исходных показателей xj(t) на t, t2. При этом в j-м столбце записаны остатки xj(t) (j = 1,…,m). Поскольку 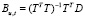 , то в j-м столбце матрицы Βu,t записаны оценки коэффициентов регрессии uj(t) на t, t2, полученные с помощью метода наименьших квадратов.
, то в j-м столбце матрицы Βu,t записаны оценки коэффициентов регрессии uj(t) на t, t2, полученные с помощью метода наименьших квадратов.
Как отмечалось выше, естественно положить прогнозные значения uj(L) равными нулю. Подставляя  в (5), с учётом (6), получаем, что ошибка прогноза
в (5), с учётом (6), получаем, что ошибка прогноза 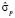 равна
равна
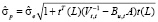 . (7)
. (7)
Если прогнозирование 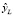 осуществляется только по оценке тренда, без учёта uj(t), то, ошибку прогноза
осуществляется только по оценке тренда, без учёта uj(t), то, ошибку прогноза 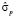 , аналогично, получаем по формуле
, аналогично, получаем по формуле
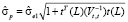 , (8)
, (8)
где 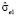 – оценка стандартной ошибки трендовой модели.
– оценка стандартной ошибки трендовой модели.
Ниже будет показано, что матрица А близка к нулевой, и тогда формулы (7) и (8) отличаются только множителем 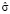 . Так как
. Так как 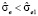 , то ошибка прогноза (7) будет меньше ошибки прогноза (8). Прогнозный интервал будет меньше примерно настолько, во сколько раз
, то ошибка прогноза (7) будет меньше ошибки прогноза (8). Прогнозный интервал будет меньше примерно настолько, во сколько раз 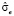 меньше
меньше 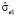 .
.
3. Согласно предположению, uj(t) не зависят от t, поэтому матрицы оценок коэффициентов регрессий t, t2 на uj(t), как и регрессий uj(t) на t, t2, близки к нулевой, 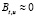 ,
, 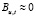 , и, следовательно,
, и, следовательно, 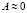 . В результате получаем
. В результате получаем
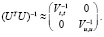 (9)
(9)
Подставляя (9) в (5) и учитывая, что 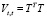 и
и 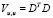 , получаем
, получаем
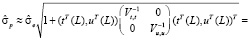
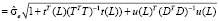 .
.
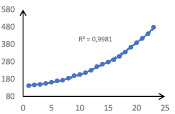
Рис. 1. График динамики Y
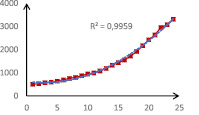
Рис. 2. График динамики X1
Возведя последнее равенство в квадрат, видим, что дисперсия прогноза распалась на два слагаемых, одно из которых не зависит от t, а другое – от uj(t).
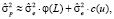 (10)
(10)
где 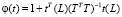 не зависит от остатков u(t), а
не зависит от остатков u(t), а 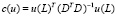 не зависит от t.
не зависит от t.
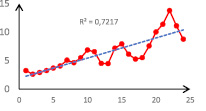
Рис. 3. График динамики X2
4. Сравним оценки прогнозов, полученные по разным моделям, на примере исследования зависимости агрегата денежной массы Y (млрд долл.) от ВНП X1 (млрд долл.) и процентной ставки по 6-месячным государственным облигациям США X2 ( %) [5]. Вычисления выполнены в программе Gretl по 24 наблюдениям (n = 24, m = 2).
Как видно из рис. 1–3, y(t) и x1(t) имеют чётко выраженные параболические тренды с достаточно большим коэффициентом детерминации R2, x2(t) имеет тренд, близкий к линейному.
Построим модель 1 – трендовую модель зависимости y(t) только от t и t2:
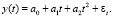
Регрессоры t и t2 сильно коррелируют, коэффициент корреляции равен 0,97. Чтобы избавиться от возможных последствий мультиколлинеарности [6], заменим в моделях t на t-tср., где tср. - среднее арифметическое значений t. Параметр t2 заменится при этом на (t-tср.)2. Тогда коэффициент корреляции между новыми t и t2 станет равным нулю.
Оценка тренда имеет вид
 ,
,
стандартная ошибка модели 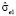 равна 6,21; коэффициент детерминации R2 = 0,997; средняя относительная ошибка аппроксимации Еотн = 7,43; стандартная ошибка прогноза при прогнозировании на шаг вперёд равна
равна 6,21; коэффициент детерминации R2 = 0,997; средняя относительная ошибка аппроксимации Еотн = 7,43; стандартная ошибка прогноза при прогнозировании на шаг вперёд равна 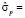 7,46.
7,46.
Построим модель 2 регрессии y(t) на исходные экзогенные переменные x1(t) и x2(t):
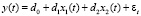 ,
,
Оцененная модель имеет вид
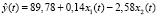 .
.
Как видно из табл. 1, все коэффициенты модели регрессии значимы на 5 % уровне.
Таблица 1
Доверительные интервалы коэффициентов модели 2
|
Переменная |
Коэффициент |
95 % доверительный интервал |
|
const |
89,78 |
(81,243, 98,312) |
|
x1 |
0,136 |
(0,128, 0,144) |
|
x2 |
–2,577 |
(–5,050, –0,104) |
Коэффициент детерминации R2 равен 0,995; стандартная ошибка модели 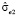 равна 8,13, средняя относительная ошибка аппроксимации Еотн = 4,18, стандартная ошибка прогноза при прогнозировании на шаг вперёд равна
равна 8,13, средняя относительная ошибка аппроксимации Еотн = 4,18, стандартная ошибка прогноза при прогнозировании на шаг вперёд равна 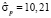 . Коэффициенты корреляции y(t) с x1(t) и x2(t) равны 0,997 и 0,856 соответственно; регрессоры мультиколлинеарны, поскольку коэффициент корреляции x1(t) с x2(t) равен 0,874. В то же время коэффициент регрессии при x2(t) отрицательный. Это следствие ложной корреляции.
. Коэффициенты корреляции y(t) с x1(t) и x2(t) равны 0,997 и 0,856 соответственно; регрессоры мультиколлинеарны, поскольку коэффициент корреляции x1(t) с x2(t) равен 0,874. В то же время коэффициент регрессии при x2(t) отрицательный. Это следствие ложной корреляции.
Построим модель 3 регрессии y(t) на t, t2 и на u1(t), u2(t) (отклонения от тренда x1(t) и x2(t)) имеет вид
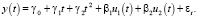
Оцененная модель имеет вид
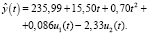
В табл. 2 приведены доверительные интервалы коэффициентов модели 3, все коэффициенты модели значимы на 5 % уровне.
Таблица 2
Доверительные интервалы коэффициентов модели 3
|
Переменная |
Коэффициент |
95 % доверительный интервал |
|
const |
235,99 |
(232,496, 239,488) |
|
t |
15,495 |
(15,173, 15,818) |
|
t2 |
0,704 |
(0,648, 0,759) |
|
u1(t) |
0,086 |
(0,0307, 0,141) |
|
u2(t) |
–2,331 |
(–4,428, –0,233) |
Коэффициенты при t и t2 модели 3, естественно, близки к коэффициентам модели 1. Точные коэффициенты при u1(t) и u2(t) модели 3, как отмечалось, совпадают с коэффициентами при x1(t) и x2(t) в модели 2. Поэтому при больших n оценки коэффициентов должны быть близки. У нас n = 24 и оценки не очень близки, оценки коэффициентов модели 3 составляют 61 % и 90 % от оценок модели 2.
Таблица 3
Метод инфляционных факторов
|
VIFj |
|
|
t |
1,000 |
|
t2 |
1,155 |
|
u1(t) |
1,877 |
|
u2(t) |
2,032 |
В модели 3 коэффициент корреляции u1(t) и u2(t) равен 0,649 и, следовательно, мультиколлинеарность отсутствует, об этом же свидетельствуют результаты тестирования на мультиколлинеарность по методу инфляционных факторов [6] (табл. 3), все VIFj < 10.
Коэффициент детерминации R2 равен 0,998; стандартная ошибка модели 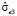 равна 5,23; средняя относительная ошибка аппроксимации Еотн = 7,01; ошибка прогноза при прогнозировании на шаг вперёд равна
равна 5,23; средняя относительная ошибка аппроксимации Еотн = 7,01; ошибка прогноза при прогнозировании на шаг вперёд равна 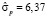 .
.
Стандартная ошибка модели 3 оказалась в 1,2 раза меньше стандартной ошибки модели 1, 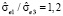 . Матрица A в (7), как и ожидалось, близка к нулевой,
. Матрица A в (7), как и ожидалось, близка к нулевой,
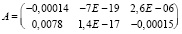 .
.
Полученные результаты моделирования по трем моделям приведены в табл. 4.
Таблица 4
Результаты моделирования
|
Модель |
Cпецификация модели |
R2 |
|
|
Еотн |
|
1 |
|
0,997 |
6,21 |
7,46 |
7,43 |
|
2 |
|
0,995 |
8,13 |
10,21 |
4,18 |
|
3 |
|
0,998 |
5,23 |
6,37 |
7,01 |
Как видим, стандартная ошибка модели 3 меньше стандартных ошибок моделей 1 и 2 в 1,19 и в 1,55 раз, ошибки прогноза по моделям 1 и 2 больше ошибок прогноза по модели 3 в 1,17 и 1,6 раза соответственно. Модель 3 оказалась предпочтительней моделей 1 и 2.
Заключение
Модифицированная трендово-факторная модель позволяет в какой-то степени решить проблему мультиколлинеарности при моделировании многомерных временных рядов, и при этом стандартная ошибка модели заведомо меньше стандартных ошибок других моделей.