Мультиколлинеарность – это проблема, с которой можно столкнуться при построении регрессионных моделей. Распознавание мультиколлинеарности и выявление ее причин часто представляют серьезную задачу в эмпирических исследованиях, поскольку, с одной стороны, негативные последствия мультиколлинеарности не всегда происходят, а, с другой стороны, мультиколлинеарность может быть вызвана не только одной переменной, но и группой переменных. Задача усложняется, если есть сильная тенденция в объясняющих переменных или если доступный объем информации слишком мал для изучения влияния объясняющих переменных на зависимую переменную. Мультиколлинеарность увеличивает дисперсию оценок коэффициентов и делает оценки очень чувствительными к незначительным изменениям в модели. В результате оценки коэффициентов нестабильны и трудно поддаются интерпретации.
Цель исследования: анализ индикаторов общей и индивидуальной диагностики коллинеарности, направленных на решение проблемы мультиколлинеарности данных, возникающей по причине высокой информационной избыточности метрических данных. Для обнаружения мультиколлинеарности среди регрессоров используются различные диагностические индикаторы. Во многих статистических программах присутствуют несколько процедур для оценки мультиколлинеарности.
Большинство индикаторов показывают, насколько исследуемые данные не идеальны, то есть в какой степени они отклоняются от «идеального случая», когда каждая объясняющая переменная линейно независима от других. Для некоторых индикаторов нет определенной границы для указания вредной степени отклонения. Интерпретация индикаторов мультиколлинеарности часто весьма субъективна. Результат методов, применяемых для уменьшения негативных эффектов мультиколлинеарности, напрямую связан со степенью распознавания мультиколлинеарности. Хотя использование большинства этих методов уменьшает или может уменьшить уровень негативных последствий мультиколлинеарности, это может сопровождаться другими отрицательными последствиями – например, вследствие значительной потери информации или неправильной интерпретируемости результатов.
Материалы и методы исследования
Для проведения исследования представляется полезным разбиение индикаторов мультиколлинеарности на две группы: реализующих общую диагностику всего массива переменных и индивидуальную диагностику [1]. Индикаторы общей диагностики помогают получить представление о существовании мультиколлинеарности, но они не указывают, какой регрессор может быть причиной коллинеарности, в то время как индикаторы индивидуальной диагностики указывают на регрессоры, вызывающие коллинеарность.
В R для обнаружения коллинеарности среди регрессоров используют пакет mctest, в нем есть две функции: omcdiag() и imcdiag(), которые реализуют диагностику общей и индивидуальной проверки мультиколлинеарности [2].
Рассмотрим использование индикаторов функции imcdiag() направленных на выявление влияния каждого регрессора на мультиколлинеарность.
Фактор инфляции дисперсии VIF (Variance Inflation Factor) и тест (TOL) являются широко используемыми мерами степени мультиколлинеарности j-й независимой переменной с другими независимыми переменными в регрессионной модели
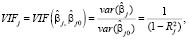
где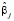 
– оценка коэффициента регрессии 
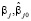– соответствующая оценка по модели с j-м регрессором, ортогональным другим независимым переменным, 
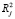– коэффициент детерминации регрессии для каждого j-го регрессора по всем остальным регрессорам.
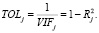
Коэффициенты дисперсии инфляции варьируются от 1 и выше. При ортогональности вектора значений признака остальным коэффициент дисперсии инфляции будет равен единице. То, насколько большим должен быть VIF, прежде чем он вызовет проблемы, является предметом обсуждения. Известно, что чем больше увеличивается VIF, тем менее достоверными будут результаты регрессии. В целом, если VIFj > 10, то j-й регрессор может привести к мультиколлинеарности. Некоторые авторы [3] предлагают более консервативный уровень 5 или даже 2,5.
Иногда высокий VIF вообще не является поводом для беспокойства, например при использовании фиктивных переменных, представляющих номинальные переменные с тремя или более категориями.
Курто и Пинто [4] указали ситуации, когда традиционный VIF будет переоценивать реальное влияние корреляции между регрессорами на дисперсию и предложили индикатор, известный как исправленный VIF (CVIF):
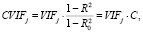
где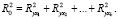 
Однако Курто и Пинто не рассматривали ситуации, когда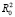 
может быть больше 1. Следствием этого будет то, что СVIFj может принимать не интерпретируемые отрицательные значения. В работе [5] предложена модификация СVIFj:
.
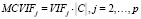Несмотря на это изменение, может возникнуть другая проблема, когда С <1, СVIFj будет меньше 1, что не соответствует определению VIFj, так как это будет означать, что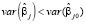 
, а это невозможно поскольку дисперсия ортогонального фактора должна быть наименьшей. Встречаются ситуации, когда применение MCVIFj и СVIFj могут дать более точное представление о мультиколлинеарности, но использование классического VIFj возможно во всех случаях, поэтому можно пренебречь тем, что иногда он будет переоценивать реальное влияние корреляции между регрессорами на дисперсию.
Результаты исследования и их обсуждение
Проанализируем использование рассмотренных индикаторов для тестирования мультиколлинеарности в задаче моделирования цены на бензин в Российской Федерации с января 2016 по сентябрь 2018. Зависимая переменная Y – цена на бензин в РФ, (USD/lit) [6]; регрессоры: X1 – курс рубля к евро; X2 – курс доллара к евро [7]; Х3 – цена на нефть Brent, (USD/barrel) [8]; X4 – цена бензина в Европе, (USD/lit) [9]; X5 – цена на бензин в США, (USD/lit); X6 – Мировое производство сырой нефти и жидкого топлива (миллионов баррелей в день) [10]. Данные получены из открытых источников.
Воспользовавшись функцией imcdiag() пакета mctest(), получим результаты индивидуальной диагностики (рис. 1).
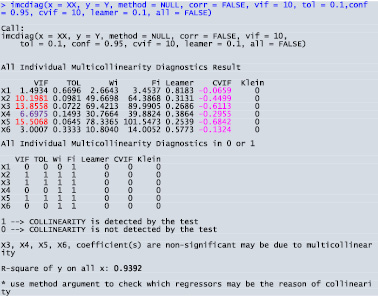
Рис. 1. Диагностика влияния каждого регрессора на мультиколлинеарность
Фактор инфляции дисперсии VIF больше 10 у Х2, Х3, Х5, у Х4 больше 5. Именно эти факторы приводят к мультиколлинеарности.
Значения индикатора CVIF для всех регрессоров отрицательные и меньше 1. Размещение индикатора CVIF в функции imcdiag() пакета mctest() не является обоснованным. Сообщение, что коэффициенты при факторах X3, X4, X5, X6 могут быть незначимы из-за мультиколлинеарности, подтверждается протоколом регрессионного анализа (рис. 2).
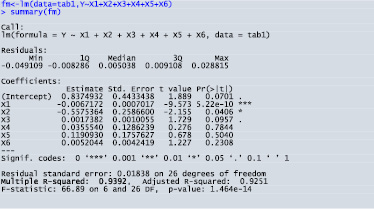
Рис. 2. Протокол регрессионного анализа
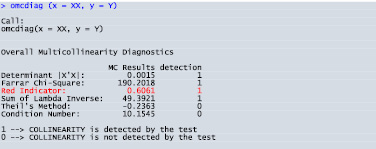
Рис. 3. Индикаторы общей диагностики мультиколлинеарности
Построенное уравнение регрессии является значимым (критерий Фишера равен 66,89, p-value: 1.464e-14), коэффициент детерминации высокий 0,939, а коэффициенты при факторах X3, X4, X5, X6 незначимы (p-value больше 0,05). Такая ситуация характерна при частичной, или нестрогой, мультиколлинеарности в данных. Этот тип мультиколлинеарности обнаружить значительно сложнее, поскольку она не является ошибкой спецификации или моделирования, на самом деле это проявление избыточности данных.
Значения VIF указывают, в какой степени каждый из факторов приводит к мультиколлинеарности:
VIF (X2 – курс доллара к евро) = 10,2;
VIF (Х3 – цена на нефть Brent, (USD/barrel) = 13,86;
VIF (X4 – цена бензина в Европе, (USD/lit) = 6,7;
VIF (X5 – цена на бензин в США, (USD/lit) = 15,51.
Протестируем на избыточность анализируемые данные с помощью функции omcdiag() пакета mctest() (рис. 3).
В функции omcdiag() реализовано несколько тестов проверки мультиколлинеарности всего массива данных [11]: проверка равенства нулю определителя корреляционной матрицы; тест Фаррара – Глоубера (первая часть, проверка наличия мультиколлинеарности всего массива переменных по критерию «хи-квадрат»); Red Indicator (красный индикатор) и другие. В данной ситуации представляет интерес значение красного индикатора, свидетельствующее об избыточности анализируемых данных. Действительно, Х3 – цена на нефть Brent, (USD/barrel) и X5 – цена на бензин в США, (USD/lit) дублируют, в какой-то степени, друг друга. В решаемой задаче исключение отдельных факторов из модели вполне обосновано.
Применяя пошаговую процедуру исключения факторов, получили трехфакторную модель регрессии (рис. 4):
.
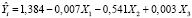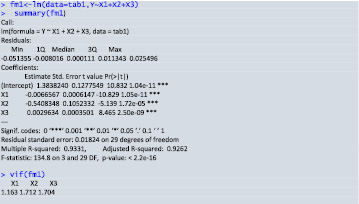
Рис. 4. Результаты последнего протокола регрессионного анализа
Анализ теста на мультиколлинеарность последней модели показал ее отсутствие.
Значения факторов инфляции от 1,16 до 1,72 (рис. 4):
VIF (X1 – курс рубля к евро) = 1,163;
VIF (X2 – курс доллара к евро) = 1,712;
VIF (Х3 – цена на нефть Brent, (USD/barrel) = 1,704.
После устранения мультиколлинеарности можно использовать полученное уравнение регрессии для ранжирования факторов по степени их влияния на зависимую переменную с помощью дельта-коэффициентов Δ(j) [12]:
,
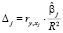где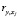 
– коэффициент парной корреляции между фактором Xj и зависимой переменной, 
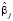– коэффициент при факторе Xj уравнения регрессии в стандартизованном виде, R2 – коэффициент детерминации. Результаты представлены в таблице.
Дельта коэффициенты
|
Δ1 |
Δ2 |
Δ3 |
|
0,379 |
0,184 |
0,477 |
Из этой таблицы можно сделать вывод, что наибольшее влияние на цену бензина в рассматриваемый период оказывает фактор Х3 – цена на нефть Brent, затем X1 – курс рубля к евро и X2 – курс доллара к евро.
Заключение
Подводя итог, можно отметить, что комплексное применение диагностических индикаторов общей и индивидуальной коллинеарности, реализованных в пакете mctest() в среде R, упрощает решение задачи выявления и устранения мультиколлинеарности. Хотя не все индикаторы, включенные в пакет, на данный момент одинаково полезны. Так, требуется модификация индикатора CVIF, разработка более обоснованных критических значений для красного индикатора. Но в целом инструменты пакета mctest() вполне пригодны для использования.