Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Одной из целей Программы «Цифровая экономика Российской Федерации», принятой в 2017 г. и рассчитанной на семь лет (2018–2024 гг.), является перевод на компьютерную основу всей информационной работы, прямо или косвенно связанной с подготовкой, принятием и реализацией управленческих решений во всех сферах и звеньях народного хозяйства [1; 2]. Для достижения этой цели должно быть решено множество задач, среди которых особо важную роль играют задачи по выявлению, описанию и анализу связей, зависимостей и тенденций в экономике.

Экономика Республики Дагестан имеет сельскохозяйственную направленность. Взаимосвязи, зависимости, тенденции в сельском хозяйстве более сложны и трудновыявляемы, чем в других отраслях экономики. Это подтверждает и настоящее исследование, целью которого является выявление тенденций в динамике показателей затрат в сельском хозяйстве региона и разработка вариантов их прогнозов. Для достижения поставленной цели решены следующие задачи: собраны данные показателей затрат в сельском хозяйстве Республики Дагестан за 2010–2016 гг. и сформировано исходное информационное обеспечение; построены модели, выражающие тенденции и их характер; рассчитаны варианты прогнозов показателей затрат в сельском хозяйстве; создан комплекс аналитических таблиц и сформулированы выводы.

Материалы и методы исследования

В качестве исходных материалов для исследования выбран ряд взаимосвязанных показателей затрат в сельском хозяйстве Республики Дагестан за семь лет (2010–2016 гг.). При выявлении тенденций в динамике взаимосвязей показателей затрат и разработке прогнозов применен системный подход, предполагающий использование взаимно дополняющих методов и модельно-компьютерных инструментариев.

Результаты исследования и их обсуждение

Одним из инструментов выявления и оценки тенденций в динамике экономических показателей являются уравнения временных рядов. По совокупности данных отдельного экономического показателя можно построить уравнение регрессии, называемое уравнением временного ряда, имеющее вид Yt = f(t), где Yt – величины экономического показателя в t-м временном периоде [3].

В настоящем исследовании нами построены уравнения временных рядов для показателей сельского хозяйства в целом, а также растениеводства и животноводства. В качестве исходных данных использованы величины затрат в аграрном секторе экономики Республики Дагестан за 2010–2016 гг.

Проведенный нами графический анализ показал, что временные ряды предположительно имеют тенденции. Но определить однозначно их виды графическим методом практически невозможно. В таких случаях проф. К.Р. Адамадзиев рекомендует строить и анализировать несколько видов уравнений [4]. Нами построены пять видов уравнений (линейного, показательного, степенного, параболического и гиперболического видов) для каждого из показателей. Наличие тенденций проверено по наиболее значимым из статистических характеристик: индексам детерминации (R), стандартным ошибкам для зависимых показателей (sey) и средним ошибкам аппроксимации (А, измеримой в процентах) для трех видов уравнений (линейного, показательного и степенного).

Согласно величинам R полностью неприемлемыми оказались три уравнения, выражающие тенденции изменения затрат на оплату труда в растениеводстве (R = 0); еще три уравнения, выражающие тенденции в динамике затрат на оплату труда в сельском хозяйстве в целом, можно считать удовлетворительно приемлемыми (0,21 < R < 0,54); остальные из построенных уравнений временных рядов имеют высокую степень приемлемости (практически во всех случаях (R > 0,90). По величине средней ошибки аппроксимации (А, %) все уравнения регрессии оказались приемлемыми (если величина А < 10 %, то соответствующее уравнение считается «хорошим» по приемлемости).

После оценки приемлемости уравнений, выражающих тенденции, следует рассчитывать и анализировать их параметры и другие показатели. Величины параметров (b, m) построенных нами уравнений временных рядов приведены в табл. 1.

Таблица 1

Величины параметров уравнений временных рядов

Особого внимания заслуживают уравнения линейного и степенного видов, параметры (m) при показателе-факторе (t) которых имеют экономический смысл:

а) в линейных уравнениях они равны предельным эффектам, определяемым по формулам производных dYt/dt и показывающим абсолютный рост зависимого показателя за 1 год;

б) в степенных уравнениях они равны коэффициентам эластичности, рассчитываемым по формулам 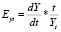и показывающим рост зависимого показателя в процентах при увеличении фактора-времени на условный процент.

В уравнениях линейного вида предельные эффекты равны параметрам при показателе-факторе t, т.е. dYt/dt = m, а в уравнениях степенного вида – коэффициенту эластичности Eyt = m.

Суммарные затраты в сельском хозяйстве можно представить в виде суммы трех составляющих Yt = MZt + ZPt + PZt, где MZt, ZPt, PZt – материальные затраты, затраты на оплату труда и прочие затраты. Иными словами по линейным уравнениям временных рядов Yt, MZt, ZPt можно строить линейные уравнения для прочих материальных затрат (PZt): PZt = Yt – MZt – ZPt. Подставляя вместе Yt, MZt, ZPt правые части построенных для них уравнений линейных видов, получим: PZt = (b – b1 – b2) + (m – m1 – m2)*t.

В соответствии с величинами параметров (b, m) из табл. 1 формулы уравнений временных рядов линейного вида для прочих затрат будут иметь следующую математическую запись:

а) для сельского хозяйства в целом

PZt = 193014 + 234446*t;

б) для растениеводства

PZRt = 209204 + 108801*t;

в) для животноводства

PZJt = 18024 + 91256*t.

С другой стороны, правомерно строить уравнения временных рядов для трех рассматриваемых видов затрат (по сельскому хозяйству в целом, материальных затрат, затрат на оплату труда) как сумму уравнений для растениеводства и животноводства:

а) все затраты

Yt = YRt + YJt;

б) материальные затраты

MZt = MZRt + MZJt;

в) затраты на оплату труда

ZPt = ZPRt + ZPJt;

В соответствии с величинами параметров (b, m) из табл. 1 нами построены следующие уравнения временных рядов:

а) для всех затрат в сельском хозяйстве

Yt = 1325262 + 882822*t;

б) для материальных затрат

MZt = 526167 + 665381*t;

в) для затрат на оплату труда

ZPt = 571867 + 27386*t;

г) для прочих затрат

PZt = 227228 + 190055*t.

Построенные уравнения можно рассматривать как системы взаимно независимых уравнений временных рядов.

По уравнениям временных рядов степенного вида можно определить величины материальных затрат и затрат на оплату труда, приходящихся на 1 тыс. руб. всех затрат в виде уравнений временных рядов (MEt, ZPEt):

;

.

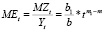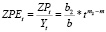Для сельского хозяйства в целом

;

.

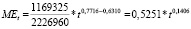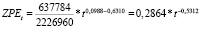Такие же уравнения, построенные нами для растениеводства и животноводства, имеют вид:

а) для растениеводства

; ;

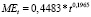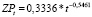б) для животноводства

; .

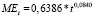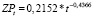Одной из главных целей выявления и математического описания тенденций в динамике экономических показателей является их использование для прогнозирования. Методику применения уравнений временных рядов для прогнозирования покажем на примере уравнений линейного и степенного видов.

До появления и широкого применения компьютерных технологий методика разработки прогнозов сводилась к их разработке на основе темповых и структурных показателей, определяемых на основе фактических данных за пять и более предыдущих временных периодов, с помощью которых оценивались тенденции в динамике того или иного экономического показателя. В настоящее время расчеты прогнозов, как правило, производятся на ЭВМ методами математического моделирования и компьютерных технологий. В частности, прогнозные расчеты можно выполнять на ПЭВМ в MS Excel двумя способами [4]:

а) по просмотренным уравнениям временных рядов, выражающим тенденции;

б) с помощью встроенных статистических функций в MS Excel, при использовании которых все прогнозные расчёты автоматически выполняются без непосредственного построения самих уравнений.

Второй способ является, с нашей точки зрения, более эффективным; при этом способе создается таблица, которая содержит две группы данных:

а) исходные или заданные данные, к которым относятся величины трех экономических показателей (Yt, MZt, ZPt) за 2010–2016 гг. и величины показателя-фактора (t) за анализируемый период и прогнозные временные периоды (t = 1,2,...,7; t = 8, 9, 10);

б) величины каждого из трех показателей за годы прогнозного периода, рассчитанные с помощью уравнений временных рядов.

Поскольку виды уравнений временных рядов, с помощью которых следует проводить прогнозные расчёты, заранее не известны, то целесообразно рассчитывать по два-три и более вариантов прогнозов, предполагая, что вид уравнения может оказаться линейным, показательным, степенным и т.д., используя системный подход [3; 5].

В MS Excel имеются три встроенные функции для автоматизированного выполнения прогнозных расчетов: «предсказ», «тенденция» и «рост». Первая и вторая функции предназначены для прогнозирования с помощью линейных уравнений, третья – с помощью уравнений показательного вида. С помощью «предсказ» («тенденция») можно рассчитывать прогнозы не только для линейных, но и для ряда нелинейных уравнений, которые могут быть преобразованы в линейный вид. Например, уравнение степенного вида Yt = b*tm можно преобразовать в линейный вид, прологарифмировав обе его части.

В этом случае создаются столбцы lgYt и lgt по заданным исходным данным, по которым рассчитываются прогнозные значения: сначала выраженные в логарифмическом виде, а затем их абсолютные величины в тыс. руб.

С помощью функции «тенденция = предсказ» можно проводить прогнозные расчеты и по уравнениям гиперболического и параболического видов.

По фактическим исходным данным за семь лет (2010–2016 гг.) можно, по нашему мнению, рассчитать прогнозы на 2–4 года. В табл. 2 приведены варианты прогнозов значений всех затрат в сельском хозяйстве РД на три года (2017–2019 гг.).

Прогнозные значения затрат нами рассчитаны и по уравнению гиперболического вида, которые подтверждают наше предположение об их неприемлемости и нежелательности. Целесообразно и следует провести сравнительную оценку на реальность, желательность и приемлемость всех рассчитанных вариантов прогнозов. Самым желательным по экономической логике при прочих равных условиях является вариант с наименьшими затратами. Таковым в нашем случае является вариант прогноза, рассчитанный по уравнению степенного вида.

Однако следует иметь в виду, что рост затрат в экономике всегда связан с необходимостью увеличения объемов производства продукции. Поэтому реальными, желательными и более приемлемыми являются прогнозы по уравнениям линейного и параболического видов. При этом обязательным условием должно быть обеспечение опережающего роста объемов производства продукции по сравнению с объемами затрат.

Таблица 2

Величины производственных затрат в сельском хозяйстве РД фактически по данным за 2016 г. и по вариантам прогнозов, рассчитанным по пяти уравнениям временного ряда на 2017–2019 гг., тыс. руб.

Нежелательным и абсолютно неприемлемым является вариант прогноза, рассчитанный по уравнениям показательного вида, в соответствии с которым объем затрат в сельское хозяйство в 2019 г., т.е. за три года, должен почти удвоиться (прирост на 98,5 %).

Можно рассчитать варианты прогнозов и другими методами. Например, на основе двух-трех построенных уравнений путем их сложения и деления на два и три соответственно:

а) линейного и степенного уравнений 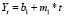; ; 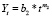после сложения обеих частей этих уравнений и деления на два получим

;

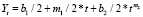б) линейного и параболического уравнения 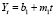; ; 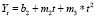после сложения и деления на два получим

.

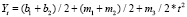Выводы

Проведенное исследование позволяет сформулировать ряд выводов: представляющих научно-практический интерес:

– сельское хозяйство – отрасль экономики РД, которой следует уделять повышенное внимание в силу двух причин: во-первых, она является трудоемкой отраслью; во-вторых, имеет высокую зависимость от природно-климатических условий. Исследования, посвященные изучению и анализу экономики сельского хозяйства как сложной системы, требуют применения арсенала различных методов (как традиционных, так и новых методов математического и компьютерного моделирования);

– в числе важных и первоочередных задач для сельского хозяйства Республики Дагестан является, с нашей точки зрения, выявление и оценка динамических тенденций в изменении экономических показателей и разработка прогнозов. Проведенное нами исследование, разработанные нами методы и модели, методика могут быть применены для решения аналогичных задач не только на уровне регионов, но и на уровне сельхозпредприятий и административных районов;

– приемлемость различных уравнений (в нашем случае четырех из пяти) для описания одной и той же тенденции позволяет разрабатывать два, три и более варианта прогнозов, на основе которых можно рассчитать более обоснованные варианты для реализации.