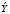Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Необходимым условием устойчивого развития государства является стабильность электроэнергетической сферы, составляющей основу функционирования экономики. Надёжное и доступное электроснабжение – неотъемлемая часть успешного конкурентного развития производства и качества жизни современного общества. Необходимость моделирования и прогнозирования спроса на электроэнергию состоит в значительных издержках, связанных с недостаточным или избыточным строительством электростанций. В условиях ужесточения экологических требований, решение о строительстве новых электростанций должно быть эмпирически обосновано [1].

Моделированию спроса на электроэнергию посвящено множество работ [2, 3]. Подробный обзор мировой эконометрической практики приведен в книге Э.Р. Берндта «Практика эконометрики: классика и современность». Автор обсуждает технику выбора инструментов эконометрических исследований на разнообразных классических и современных статистических данных. В частности, для моделирования спроса на электроэнергию приводятся данные временных рядов по США за 1951–1984 гг., заимствованные из работы Нельсона – Пека (Nelson, Peck) [4]. В книге предлагается приобрести навыки построения и исследования эконометрических моделей, опираясь на опыт авторов статьи.

Данная статья посвящена вопросам методики проверки адекватности модели прогнозирования спроса на электроэнергию Фишера – Кайсена (F.M. Fisher, C. Kaysen) в Excel. Выбор табличного процессора MS Excel обусловлен тем, что он является наиболее доступным средством для числовой обработки экономической информации и особенно эффективен на этапе изучения эконометрических методов [5].

Материалы и методы исследования

В качестве модели прогнозирования спроса на электроэнергию выбрана спецификация множественной линейной регрессии:

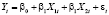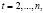, (1)

с переменными:

,

,

,

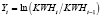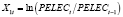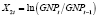где KWH – общее количество электроэнергии, используемой всеми потребителями за год (в млн киловатт-часов); PELEC – средняя цена электроэнергии за 1 кВТ•час (в центах); GNP – валовой национальный продукт США (в млн долл.). Формирование переменных в форме процентных изменений позволяет решить проблему мультиколлинеарности. Уравнения наблюдений модели (1) в матричной форме:

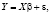
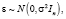
где Y – (n×1) – вектор-столбец значений эндогенной переменной, X – (n×k)-матрица регрессоров, ε – (n×1)-вектор-столбец возмущений, β – (k×1)-вектор-столбец параметров модели, σ2 – дисперсия возмущений, In – (n×n)-единичная матрица, n – объем выборки, k – число параметров модели. Модель оценивается методом наименьших квадратов (значок «Т» означает операцию транспонирования):

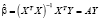(2)

– МНК-оценки параметров,

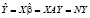(3)

– оценки (прогнозы) вектора значений эндогенной переменной.

Точное совпадение фактических данных и прогнозных значений – явление маловероятное. Оценки и прогнозы эндогенных переменных не совпадают с их истинными значениями в силу разных причин: ограниченность выборочных данных, ошибки спецификации (пропуск существенных регрессоров, неправильный выбор уравнения регрессии), ошибки измерений. Обозначим [6]: вектор остатков регрессии (отклонений на интервале оценивания, t ≤ n)

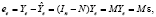
где 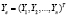, , 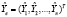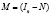идемпотентная матрица, вектор ошибок прогнозов (отклонений на интервале прогнозирования, например, для t > n)

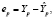
где

, ,

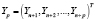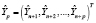p – период упреждения. Автоковариационная матрица вектора отклонений 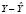для любого интервала:

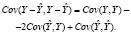(4)

На интервале оценивания:

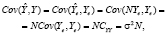(5)

поэтому автоковариационная матрица вектора остатков (4), с учетом (5), принимает вид:

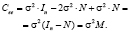(6)

На интервале прогнозирования:

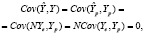(7)

в силу некоррелированности возмущений в различных наблюдениях, поэтому автоковариационная матрица вектора ошибок прогнозов, с учетом (4)–(7) равна

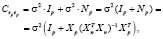(8)

где Xp – матрица регрессоров на интервале прогнозирования, Xn – матрица регрессоров на интервале оценивания. Несмещенная оценка дисперсии возмущений, вычисляемая через вектор остатков регрессионной модели

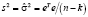, (9)

позволяет оценить автоковариационные матрицы всех случайных векторов.

Проверка адекватности модели по выборочным данным базируется на построении интервальных оценок. Для построения интервальной оценки эндогенной переменной на интервале прогнозирования, применяется процедура трансформации дроби Стьюдента

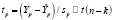
в интервальную оценку

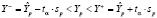, (10)

где 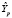– прогноз значения эндогенной переменной для момента t = p > n, tα – квантиль уровня значимости α, Yp – истинное значение эндогенной переменной на момент t = p, sp – стандартная ошибка прогноза, 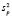– оценка дисперсии ошибки прогноза – диагональный элемент оценки матрицы (8) ( 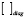– диагональный элемент матрицы):

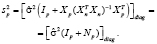(11)

Алгоритм проверки адекватности модели состоит из следующих шагов [7]:

1) результаты наблюдений разделяют на две части: обучающую (90–95 % наблюдений) и контролирующую выборки (оставшиеся наблюдения);

2) по обучающей выборке выполняется оценка параметров модели (по формуле (2));

3) по оцененной модели строится прогноз значений эндогенной переменной из контролирующей выборки и доверительные интервалы для их истинных значений (формулы: (3), (9), (11), (10));

4) выполняется проверка: если значения эндогенной переменной из контролирующей выборки накрываются доверительными интервалами – модель признается адекватной, в противном случае подлежит доработке.

Результаты исследования и их обсуждение

Для оценки модели использованы ежегодные данные временных рядов по данным США за 1951–1984 гг. В качестве обучающей выборки в работе [4] предлагается использовать наблюдения с 1951 по 1973 г. (n = 22), контролирующей – с 1974 г. по 1984 г. (p = 11).

Результаты оценивания модели по обучающей выборке в Excel при помощи функции ЛИНЕЙН приведены в табл. 1.

Таблица 1

Результат функции ЛИНЕЙН

,

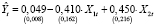s = 0,02, R2 = 0,474, F = 8,560. (12)

Прогноз эндогенной переменной по значениям регрессоров из контролирующей выборки по формуле (12) приведен в табл. 2.

Для построения доверительных интервалов значений эндогенной переменной, необходимо вычислить стандартные ошибки прогнозов по формуле (11). Для вычисления Np в Excel используются функции ТРАНСП, МУМНОЖ и МОБР категорий «Ссылки и массивы» и «Математические» соответственно. В табл. 3 представлены значения диагональных элементов проекционной матрицы Np, значения стандартных ошибок прогнозов, левая и правая границы доверительных интервалов и истинные значения эндогенной переменной.

Как следует из табл. 3, значения эндогенных переменных из контролирующей выборки накрываются доверительными интервалами для всех рассматриваемых наблюдений. Это подтверждает адекватность модели Фишера – Кайсена спроса на электроэнергию.

Реализация матричного алгоритма в Excel затратна по времени. Поэтому для вычисления стандартных ошибок прогнозов на практических занятиях рекомендуется использовать легко реализуемый метод Салкевера (Salkever) [8, 9].

В методе Салкевера, для оценки стандартной ошибки прогноза на момент t = n + 1, в матрицу регрессоров добавляется строка значений регрессоров Xt и столбец фиктивных переменных

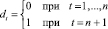, (13)

в вектор-столбец значений эндогенной переменной добавляется значение Yn+1. По сформированным таким способом данным, при помощи функции ЛИНЕЙН, оценивается модель, проверяемая на адекватность. Если исходная спецификация включает свободный член, то он учитывается параметром КОНС = 1. Стандартный протокол функции ЛИНЕЙН включает ошибку прогноза на момент t = n + 1 – оценка параметра при фиктивной переменной (13) и стандартную ошибку прогноза – стандартная ошибка параметра при фиктивной переменной. Справедливость этого утверждения можно показать на модели с фиктивной переменной [10]:

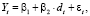
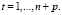(14)

Упорядочим наблюдения таким образом, что, dt = 0 при t = 1,...,n, dt = 1, при, 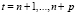. Обозначим

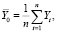
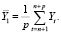
В соответствии с (2)

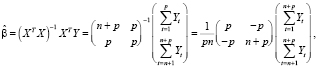
где

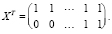
Таким образом, оценка свободного члена модели (14) равна

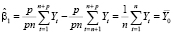, (15)

оценка параметра при фиктивной переменной:

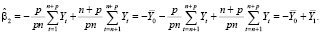(16)

Автоковариационная матрица оценок параметров:

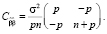
С учетом структуры вектора Y в методе Салкевера, для периода упреждения p = 1:

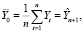
где 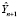– прогноз значения эндогенной переменной модели;

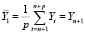
– значение эндогенной переменной на интервале прогнозирования. Таким образом, оценка параметра (16) при фиктивной переменной равна ошибке прогноза эндогенной переменной:

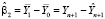, (17)

и, следовательно, дисперсия оценки параметра при фиктивной переменной равна дисперсии ошибки прогноза (с учетом некоррелированности ошибок):

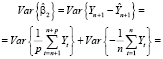
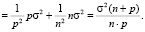(18)

В соответствии с (11), дисперсия ошибки прогноза вычисляется по формуле

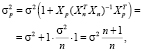(19)

где 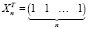, 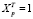. С учетом значения p = 1, формула (18) дисперсии оценки параметра при фиктивной переменной для модели (14) принимает вид (19) и совпадает с дисперсией ошибки прогноза. Этот же результат подтверждается эмпирической проверкой. Сформируем вспомогательную матрицу регрессоров с блочной структурой [11]:

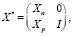
где Xn – (n×k)-матрица значений регрессоров из обучающей выборки (n = 22), Xp – (p×k)-матрица значений регрессоров из контролирующей выборки (p = 3), 0 – (n×p) – нулевая матрица, I – (p×p)-единичная матрица. В табл. 4 приведены элементы вспомогательной матрицы X* для контролирующей выборки, включающей три наблюдения.

Таблица 4

Вспомогательная матрица регрессоров

В табл. 5 приводится протокол оценки модели спроса на электроэнергию (1) при помощи функции ЛИНЕЙН методом Салкевера.

Заключение

Сравнение результатов оценивания с табл. 1 и 3 (третий столбец) показывает, что оценки параметров и их стандартные ошибки при регрессорах [ ]diag исходной модели и вспомогательной модели Салкевера совпадают. Стандартные ошибки оценок параметров при фиктивных переменных (отмеченные жирным шрифтом в табл. 5) равны стандартным ошибкам прогнозов, приведенных в табл. 3, используемым для построения интервальных оценок в алгоритме проверки адекватности, но их вычисление намного эффективнее матричного метода при реализации в Excel.