Анализ сложных социально-экономических многопараметрических систем и процессов в них в виде линейных математических моделей не приводит к адекватному описанию. При изучении рынка трудовых ресурсов, производственного, финансового и других в макроэкономическом анализе часто используют методы оптимизации, теории исследования операций или системы линейных квазиравновесных уравнений баланса. Однако экономические и социальные системы часто непредсказуемы в своём развитии, предполагающем возможность реализации нескольких различных вариантов. Используемый принцип оптимальности не описывает такие явления, как автоколебания параметров систем, наличие у них быстрых изменений, скачков и поведения типа динамического хаоса. Для изучения таких процессов требуются нелинейные синергетические подходы [1–3].
В рыночной макроэкономике социально-экономические системы (СЭС) считаются открытыми, неравновесными и участвующими в обмене ресурсами, информацией и энтропией с другими системами. Обмен энтропией с окружением может приводить к её локальному понижению в СЭС. Это ведёт к структурным изменениям в организации и образованию новых форм функционирования систем и взаимодействия с окружением. В структуре поведения СЭС иногда возникают странные аттракторы с динамическим хаосом и процессами самоорганизации новых эволюционно изменяющихся структур. Для описания открытой неравновесной СЭС необходимо решение модели из нескольких динамических, связанных нелинейных дифференциальных уравнений для медленно меняющихся параметров порядка (ПП), моделирующих поведение связанных рынков производства товаров, трудовых ресурсов, финансов, услуг и т.д. Ранее нами рассматривалось регулярное и стохастическое поведение открытых многосекторных моделей макроэкономических систем как систем дифференциальных уравнений для ПП экономики при изучении синергетических систем [1, 3].
Нашей задачей является исследование сценариев динамического изменения социально-экономических систем с учётом различных экономических и социальных факторов, внешних воздействий и возможности управления процессами в них. В структуре и поведении открытых синергетических систем зачастую возникает череда хаотических состояний, описываемых странными аттракторами. Они характеризуются дробной фрактальной структурой, которая может менять фрактальную размерность с течением времени. Хаотическое поведение фазовых траекторий в пространстве состояний систем иногда превращается в колебания экономических и социальных параметров или показывает поведение типа седла, устойчивых или неустойчивых узлов или фокусов. Поэтому целью управления развитием СЭС является обеспечение такого характера переходных процессов, которые приводят к желаемому аттрактору и переходу к движению в эволюционном режиме при выходе из аттрактора [1, 4, 5].
Синергетические модели процессов в социально-экономических системах
Дифференциальные уравнения – это естественный способ описания моделей процессов в природе и обществе, пользуясь которыми можно однозначно предсказывать будущее по известным начальным состояниям параметров. Однако известно, что эволюция социальных систем часто бывает непредсказуемой, хаотичной. Поэтому следует использовать системы динамических, связанных, нелинейных, дифференциальных уравнений с параметрами, так как для них возможны так называемые бифуркации, катастрофы. Поведение синергетической открытой многосекторной модели функционирования социально-экономической системы как системы дифференциальных уравнений для основных параметров порядка секторов макроэкономики рассмотрено нами на конкретных примерах ранее [3].
Особенностью рассматриваемых социально-экономических систем, отличающей их от технических или естественнонаучных систем, является существование большого числа скрытых управляющих параметров. Скрытые параметры могут быть выявлены в ходе исследований открытых социологических и экономических данных с применением факторного и корреляционного анализа. Выявление этих параметров входит в задачу верификации моделей и позволяет предсказывать следствия для изменений в СЭС [1, 3, 4].
Исследование устойчивости моделей социально-экономических систем
Предполагаем, что состояние СЭС характеризуется векторной переменной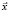 
и управляющим n-мерным параметром 
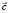, изменение которого влияет на поведение переменных 
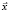. Пространство изменения 
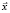и параметров 
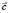называется фазовым пространством. Изменение во времени вектора переменных 
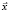, при наличии поля управляющих параметров 
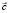характеризуется скоростью 
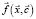, значение которой в градиентном приближении можно выразить через синергетический потенциал СЭС 
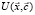в виде [1, 6]
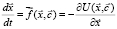. (1)
Рассмотрим равновесное или квазистационарное состояние СЭС, которое в одномерном случае задаётся уравнением f(x(с), с) = 0. При заданном параметре с однозначное разрешение уравнения стационарности даёт кривую равновесных состояний систем в фазовом пространстве x = x(c). Однако при нарушении условий разрешимости уравнения стационарности в точке (x0, c0) возможно появление новой стационарной ветви решения (1) в фазовом пространстве, т.е. происходит бифуркация (раздвоение) кривых равновесия [6].
При изменении параметров модели ci возможно появление тройных, четверных и т.д. критических точек, т.е. возникновение многих новых ветвей решения модели (1). В связи с этим в теории бифуркации приходится решать вопрос о возможных сменах моделей функционирования и смене структур СЭС. Таким образом, переход систем через критические точки ci0 при изменении параметров ci сопровождается неоднозначностью выбора дальнейшего поведения систем. Ситуация осложняется появлением у части ветвей структурной неустойчивости. Под структурной устойчивостью СЭС понимают неизменность бифуркационной картины системы при малых изменениях параметров модели.
Поскольку вблизи критических точек системы входят в область сильных флуктуаций, то при переходе на структурно неустойчивую фазовую траекторию возможно появление череды неустойчивостей и, следовательно, трудностей с управлением системами в области критических точек. Компьютерное моделирование простейших синергетических моделей, однако, показывает, что возникновение лавин хаотических бифуркаций чередуется с периодами спокойного эволюционного развития [1, 6].
Следствием описания бифуркационного поведения нелинейных многопараметрических синергетических моделей СЭС нужно считать следующую программу исследования при изучении конкретных моделей. Во-первых, необходимо проведение бифуркационного анализа, состоящего в выявлении критических точек на фазовых траекториях; выявление наличия устойчивых ветвей при прохождении критических точек. Во-вторых, проведение анализа на устойчивость возможных траекторий моделей СЭС после прохождения критических точек, что позволяет сделать теория катастроф [1, 5, 6].
В динамике явлений в СЭС процесс изменения синергетического потенциала U связан с изменениями самой системы вдоль её траекторий в фазовом пространстве. Поэтому необходимо исследовать для всех значений параметров в фазовой плоскости особые точки функции U и проследить за характером трансформации стационарных особых точек. Процесс выхода из аттракторов на эволюционную траекторию сопровождается поглощением интенсивности одних степеней свободы другими, которые называются в теории неравновесных фазовых переходов параметрами порядка. Синергетическая модель изучаемого явления должна быть системой дифференциальных уравнений для параметров порядка xi, включая для СЭС уравнения для основных управляющих параметров ci.
Синергетическая модель рынка труда
Рынок труда, подчиняясь законам спроса и предложения, по механизмам и принципам своего функционирования является рынком особого рода, который имеет существенные отличия в своей структуре от других рынков. Регуляторами на нём являются как экономические факторы, например, спрос на рабочую силу, заработная плата, так и социально-психологические. В реальной экономической ситуации существенными факторами динамики рынка труда в сфере предложения являются: степень экономической и социальной активности различных социальных и этнических групп трудоспособного населения, гендерный фактор и т.д. На динамику рынка рабочей силы большое влияние оказывают процессы миграции. Со стороны спроса основным фактором динамики рынка труда и занятости в (СЭС) является фаза экономических циклов и коньюктура рынка. Большое влияние на спрос и потребность в рабочей силе оказывают такие факторы, как научно-технический прогресс, появление новых производственных и информационных технологий и др. [1, 5].
Будем полагать, что рынок трудовых ресурсов релаксирует медленнее, чем рынки производственный и финансовый и др., и потому является параметром порядка нашей задачи. Характеристики производства, финансового рынка и управляющие социальные и социально-психологические параметры будут входить в нелинейные уравнения для параметра порядка как квазиравновесные величины. Поскольку рынок труда сегментирован, будем рассматривать концентрацию работников xi занятых в i-м сегменте. Учитывая нелинейные члены не выше квадратичных по параметру порядка в (1), для модели xi получим
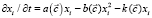, (2)
здесь a(c) – коэффициент самовоспроизводства ресурса, b(c) – коэффициент, учитывающий конкуренцию на рынке труда, k(c) – коэффициент влияния социальных и психологических факторов на рынок, таких как уровень жизнесберегающих технологий, которые позволяют защищать, лечить, кормить людей, т.е. увеличивать среднюю продолжительность жизни. К таким факторам, например, относятся: уровень развития информационных цифровых технологий в экономике, культурный уровень населения. К культурным факторам относятся, например, гендерные отношения, уровень женской эмансипации и грамотности и т.д.
Переходя к безразмерным переменным в модели (2), можно перейти к виду аналогичному «мягкой модели» исследования популяций животных в природе, предложенной в [7]. Такая модель называется системой с обратной связью, в которой последний член в правой части (2) ответственный за социальные и психологические внешние факторы, коррелируя с первым членом, корректирует плотность рабочей силы в i-том секторе. Области возможных решений (2) и возможные фазовые траектории даются кривыми на рис. 1. Как видно, плотность ресурсов стремится при любых ненулевых начальных состояниях со временем к устойчивому состоянию В, определяемому комбинацией экономических и социальных факторов. Сама устойчивая точка В является пересечением параболы нелинейного ограничения скорости роста y за счёт конкуренции на рынке и прямой kx – описывающей влияние социальных факторов. При больших коэффициентах k, определяющих коэффициент наклона линии, возможна ситуация отсутствия пересечения линий и потери устойчивости концентрации сектора трудовых ресурсов. Это участь многих профессий, вытесненных современными технологиями, экологическими запретами и т.д.
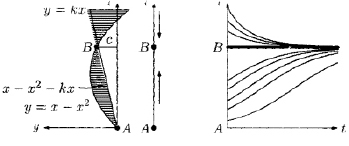
Рис. 1. Фазовые траектории и область существования решений уравнения (2) [7]
В теории катастроф синергетический потенциал СЭС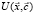 
уравнения (1) приводится к одному из канонических видов и даёт классификацию потенциалов динамических СЭС с точки зрения их устойчивого поведения вблизи точек равновесия. Вблизи стационарных точек потенциал представляется в виде степенных рядов по малым отклонениям параметров от значений в стационарных точках (xi – xi0). Основным результатом теории катастроф является доказательство утверждения, что при степенях параметров в потенциалах r ≤ 4 семейство сингулярностей структурно устойчиво и принадлежит одному из семейств по классификации теории катастроф. Основные приложения теории катастроф в науке и технике принадлежат к катастрофам типа «сборка» и »складка» [1, 6]. Рассмотренная выше задача управления трудовыми ресурсами и относится к катастрофам типа «складка».
Модель социальных катастроф
Катастрофа типа «сборка», описывающая с помощью синергетического потенциала социальные эксцессы, может иметь вид
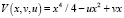, (3)
где x – удельное количество беспорядков и правонарушений, u – параметр разочарования, безысходности людей, v – параметр социальной напряжённости. Потенциал (3) имеет критические, дважды вырожденные и трижды вырожденные критические точки катастроф, которые определяются уравнениями, полученными приравниванием нулю соответственно первой, второй и третьей производной функции потенциала (3). Находя из них x, получим бифуркационную диаграмму катастрофы «сборка» в виде полукубической параболы (рис. 2).
Беспорядки (забастовка, бунт) происходят при пересечении фазовыми траекториями линии бифуркаций при росте разочарования u и безысходности v в виде скачка параметра порядка. Предотвращение беспорядков сводится к мероприятиям по улучшению социального положения. Это позволяет выбрать траекторию движения в фазовом пространстве в обход линий катастроф, где имеем скачкообразное усилении протестов, забастовок и беспорядков.
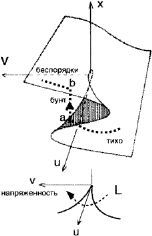
Рис. 2. Социальная катастрофа типа «сборка»
Модель динамического хаоса
Модели сложных экономических и социальных систем при некоторых условиях демонстрируют поведение типа динамического хаоса. Рассмотрим модель изменения психологии и поведения учащихся в учёбе, быту и жизни. Пусть x – характеристика отношений в быту (семья, общежитие), y – состояние отношений на учёбе (школа, вуз), z – общая характеристика психического состояния учащихся. Положим, что знак (–) у параметров задачи означает способность бороться с негативными явлениями и знак (+) означает отсутствие борьбы с ними. Модель поведения учащихся и их психическое состояние можно представить в виде системы трёх уравнений для ПП (4). Введём коэффициенты корреляции факторов параметрами σ, r, b. Эти коэффициенты определяют личности и их отношение к процессам в быту и общение с окружением. Предложенная модель имеет вид
,
,
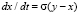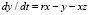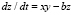, (4)
где σ, r, b – параметры модели, требующие верификации в каждом отдельном случае. Первое уравнение описывает состояние бытовых отношений, в большой степени зависящее от места учёбы. Второе уравнение отражает как отношения в быту и учебном коллективе, так и деловые качества учащихся. Третье уравнение системы (4) отражает возможности управлять своей психикой. Система уравнений (4) является стандартной моделью, предложенной Лоренцем, демонстрирующей хаотическое поведение атмосферы в метеорологии [1, 8].
Система уравнений (4) обладает неустойчивостями фазовых траекторий при r = 28, σ = 10 и b = 8/3. Компьютерное моделирование показывает, что фазовые траектории вращаются вокруг одного из неустойчивых фокусов в виде витков с растущей амплитудой. Далее система оставляет этот фокус и переходит ко второму фокусу, начиная описывать новую раскручивающуюся спираль. При этом время нахождения у каждого фокуса распределяется случайным образом и указывает на неустойчивое хаотическое состояние. В нашей модели это указывает на возможное шизофреническое, психопатическое поведение учеников при определённых условиях. Таким был первый странный аттрактор в метеорологии, который впоследствии стал популярной математической моделью динамического хаотического поведения открытых нелинейных сложных систем, к которым относится человек и общество [1, 6].
Заключение
В прошлом веке экономика и социология базировались на основе факторного или регрессионного анализа. Теперь, при описании и моделировании сложных, открытых, нелинейных систем проводятся исследования синергетических моделей хаоса, фрактальных структур и диссипативных синергетических моделей. Синергетика в этом веке уже занялась процессом моделирования экономики. Но наиболее впечатляющими будут результаты синергетического моделирования социально-экономических явлений, претендующих на роль стратегического историковедения и компьютерного прогнозирования в гуманитарных науках и обществе.