Постановка экономической проблемы и её качественный анализ требует формулировки сущности проблемы, принимаемые предпосылки и допущения. Для изучения трудовых ресурсов необходимо выделить важнейшие его характеристики и свойства моделируемого объекта, исследовать его структуру и взаимосвязь его элементов. Математические методы позволяют это сделать и упорядочить саму систему сбора и представления информации. Экономико-математическое моделирование позволяет находить решение принципиально новых научных и практических задач в любой сфере экономики.
Имеется несколько организаций и типов трудовых ресурсов. У каждой организации есть свои предпочтения среди трудовых ресурсов. Каждая организация выстраивает тип трудовых ресурсов в порядке уменьшения интереса организации к ним. Трудовые ресурсы также могут ранжировать организации по привлекательности условий труда в каждой. Исходя из имеющихся данных, требуется найти компромиссное распределение трудовых ресурсов по организациям, при котором не найдется двух и более организаций, которые захотят поменяться своими трудовыми ресурсами. При этом организации могут нанимать одновременно несколько трудовых ресурсов, но в каждую организацию должен попасть хотя бы один тип.
Алгоритм определения компромиссного распределения
Пусть N – количество организаций, M – количество трудовых ресурсов [1]. Алгоритм определения компромиссного распределения трудовых ресурсов по организациям будет выглядеть следующим образом:
Шаг 1. Каждая организация приписывает всем трудовым ресурсам веса, с помощью которых организации сортируют трудовые ресурсы по привлекательности. Организация приписывает наибольший вес трудовым ресурсам, которые для нее больше всех привлекательны. Аналогичные веса приписывает каждый из представителей трудовых ресурсов всем организациям. Данные веса можно интерпретировать как выигрыши организаций и трудовых ресурсов в зависимости от того, в какую организацию назначаются трудовые ресурсы.
Шаг 2. Строятся всевозможные варианты распределения трудовых ресурсов по организациям при выполнении следующих условий: одна организация может нанимать одновременно несколько трудовых ресурсов и в каждую организацию должен быть назначен хотя бы один представитель трудовых ресурсов. Пусть количество различных вариантов распределения трудовых ресурсов по организациям равно p.
Шаг 3. Для каждого i-го варианта распределения трудовых ресурсов по организациям определяются значения приоритетов каждого участника распределения, 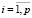 . Данные записываются в виде векторов
. Данные записываются в виде векторов 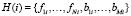 , где fji – выигрыш j-й фирмы в i-м варианте, bki – выигрыш k-х трудовых ресурсов в i-м варианте распределения трудовых ресурсов по организации,
, где fji – выигрыш j-й фирмы в i-м варианте, bki – выигрыш k-х трудовых ресурсов в i-м варианте распределения трудовых ресурсов по организации, 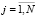 ,
, 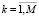 .
.
Шаг 4. Определяется максимальное значение выигрыша для каждого участника распределения среди всех вариантов распределения трудовых ресурсов по организациям 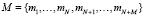 .
.
Шаг 5. Определяются отклонения: 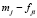 ,
, 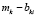 .
.
Шаг 6. Ищется значение 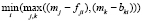 .
.
Значению i, при котором достигается данный минимум, будет соответствовать компромиссное распределение трудовых ресурсов по организациям, в котором не найдется двух и более организаций, которые захотят поменяться своими трудовыми ресурсами [2].
Динамическая задача
Если трудовые ресурсы назначаются в организации на фиксированное одинаковое для всех время и после очередного распределения трудовых ресурсов по организациям появляются новые трудовые ресурсы или организации, тогда и организации, и трудовые ресурсы будут вынуждены поменять все выставленные ими веса с учетом новых организаций и трудовых ресурсов. При этом распределение трудовых ресурсов по организациям придется проводить заново, учитывая измененные веса [3].
Рассмотрим численный пример применения алгоритма компромиссного распределения трудовых ресурсов по организациям. Допустим, необходимо распределить три типа трудовых ресурсов по трем организациям. Соответствующие данные представлены в табл. 1 и 2.
Таблица 1
Веса организаций для трудовых ресурсов
|
Организации |
Вес первого типа |
Вес второго типа |
Вес третьего типа |
|
Организация 1 |
2 |
3 |
1 |
|
Организация 2 |
8 |
5 |
9 |
|
Организация 3 |
3 |
6 |
4 |
Таблица 2
Веса трудовых ресурсов для организаций
|
Трудовые ресурсы |
Вес первой организации |
Вес второй организации |
Вес третьей организации |
|
Трудовые ресурсы 1 |
3 |
4 |
7 |
|
Трудовые ресурсы 2 |
5 |
2 |
1 |
|
Трудовые ресурсы 3 |
3 |
2 |
5 |
У каждой организации заданы веса для трудовых ресурсов, в свою очередь, у каждого типа трудовых ресурсов заданы веса организаций [4]. В табл. 3 строятся все возможные варианты распределения трудовых ресурсов по организациям.
Таблица 3
Варианты распределения трудовых ресурсов по организациям
|
Номер варианта распределения трудовых ресурсов (ТР) по организациям |
Организация 1 |
Организация 2 |
Организация 3 |
|
1 |
Тип ТР 1 |
Тип ТР 2 |
Тип ТР 3 |
|
2 |
Тип ТР 1 |
Тип ТР 3 |
Тип ТР 2 |
|
3 |
Тип ТР 2 |
Тип ТР 1 |
Тип ТР 3 |
|
4 |
Тип ТР 2 |
Тип ТР 3 |
Тип ТР 1 |
|
5 |
Тип ТР 3 |
Тип ТР 1 |
Тип ТР 2 |
|
6 |
Тип ТР 3 |
Тип ТР 2 |
Тип ТР 1 |
Таблица 4
Значения выигрышей для участников распределения
|
Организация 1 |
Организация 2 |
Организация 3 |
Тип ТР1 |
Тип ТР2 |
Тип ТР3 |
|
|
H(1) |
2 |
5 |
4 |
3 |
2 |
5 |
|
H(2) |
2 |
9 |
6 |
3 |
2 |
2 |
|
H(3) |
3 |
8 |
4 |
5 |
4 |
5 |
|
H(4) |
3 |
9 |
3 |
5 |
2 |
7 |
|
H(5) |
1 |
8 |
6 |
3 |
4 |
2 |
|
H(6) |
1 |
5 |
3 |
3 |
2 |
7 |
Для каждого варианта распределения трудовых ресурсов по организациям определяются значения выигрышей для всех участников распределения (табл. 4).
Определяются максимальные выигрыши всех участников M = [3, 9, 6, 5, 4, 7]. В табл. 5 представлены результаты определения отклонения выигрыша от максимума для каждого участника во всех вариантах распределения трудовых ресурсов по организациям [5].
Таблица 5
Результаты определения отклонения выигрыша от максимума
|
Вариант распределения |
Организация 1 |
Организация 2 |
Организация 3 |
Тип ТР1 |
Тип ТР2 |
Тип ТР3 |
|
1 |
1 |
4 |
2 |
2 |
2 |
4 |
|
2 |
1 |
0 |
0 |
2 |
2 |
5 |
|
3 |
0 |
1 |
2 |
0 |
0 |
2 |
|
4 |
0 |
0 |
3 |
0 |
2 |
0 |
|
5 |
2 |
1 |
0 |
2 |
0 |
5 |
|
6 |
2 |
4 |
3 |
2 |
2 |
0 |
Для каждого варианта распределения выбирается максимальное значение выигрышей среди всех участников (табл. 6).
Среди всех максимальных выигрышей выбирается минимальный (2), который достигается при третьем варианте (i = 3) распределения, т.е. 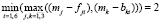 .
.
Таким образом, найдено компромиссное распределение трудовых ресурсов по организациям, при котором в первую организацию отправляется второй тип трудовых ресурсов, во вторую организацию отправляется первый тип трудовых ресурсов, а в третью организацию отправляется третий тип трудовых ресурсов [6].
Таблица 6
Максимальное значение выигрышей
|
Вариант распределения, i |
Максимальный выигрыш |
|
1 |
4 |
|
2 |
5 |
|
3 |
2 |
|
4 |
3 |
|
5 |
5 |
|
6 |
4 |
Соответственно выигрыши всех участников будут следующими: у организации 1 выигрыш 3; у организации 2 выигрыш 8; у организации 3 выигрыш 4; у типа трудовых ресурсов 1 выигрыш 4; у типа трудовых ресурсов 2 выигрыш 5; у типа трудовых ресурсов 3 выигрыш 5.
Исследование равновесия по Нэшу
В данной постановке задачи в каждом варианте распределения трудовых ресурсов по организациям учитывается тот факт, что при назначении i-й типа трудовых ресурсов в j-ю организацию, данные трудовые ресурсы и организация убираются из рассмотрения. Соответственно, у оставшихся участников становится меньше вариантов выбора организаций и трудовых ресурсов. Такие образом, в данной постановке задачи стратегии всех участников зависят друг от друга. Следовательно, найти равновесие по Нэшу в данном случае не представляется возможным [7].
Исключением в данном случае может быть ситуация, когда для каждого типа трудовых ресурсов существует только одна организация, в которой данный тип трудовых ресурсов может найти работу. Такое распределение трудовых ресурсов по организациям является равновесным по Нэшу.
Рассмотрим пример определения типа распределение трудовых ресурсов по организациям. Пусть имеется 3 организации: деревообрабатывающая, металлопрокатная, фармацевтическая. По ним нужно распределить 3 типа трудовых ресурсов: плотники, металлурги, фармацевты. Соответственно, плотники принесут наибольший выигрыш всем участником, только если будут работать на деревообрабатывающую организацию, аналогично металлурги принесут наибольший выигрыш, работая на металлопрокатную организацию, а фармацевты – на фармацевтическую организацию. Таким образом, данное распределение трудовых ресурсов по организациям является равновесным по Нэшу, так как изменение стратегии одного участника приведет к уменьшению выигрышей всех участников распределения трудовых ресурсов по организациям (табл. 7 и 8).
Таблица 7
Распределения выигрышей трудовых ресурсов
|
Тип трудовых ресурсов |
Выигрыш, если назначены в деревообрабатывающую организацию |
Выигрыш, если назначены в металлопрокатную организацию |
Выигрыш, если назначены в фармацевтическую организацию |
|
Плотники |
100 |
10 |
10 |
|
Металлурги |
10 |
100 |
10 |
|
Фармацевты |
10 |
10 |
100 |
Таблица 8
Распределения выигрышей организаций
|
Организация |
Выигрыш, если назначены плотники |
Выигрыш, если назначены металлурги |
Выигрыш, если назначены фармацевты |
|
Деревообрабатывающая |
1000 |
100 |
100 |
|
Металлопрокатная |
100 |
1000 |
100 |
|
Фармацевтическая |
100 |
100 |
1000 |
Строятся все варианты распределения трудовых ресурсов по организациям и определяются выигрыши участников (табл. 9–10).
Таблица 9
Варианты распределения трудовых ресурсов по организациям
|
Номер варианта распределения типа трудовых ресурсов по организациям |
Деревообрабатывающая |
Металлопрокатная |
Фармацевтическая |
|
1 |
плотники |
металлурги |
фармацевты |
|
2 |
плотники |
фармацевты |
металлурги |
|
3 |
металлурги |
плотники |
фармацевты |
|
4 |
металлурги |
фармацевты |
плотники |
|
5 |
фармацевты |
плотники |
металлурги |
|
6 |
фармацевты |
металлурги |
плотники |
Таблица 10
Общее распределение
|
Вариант распределения |
Деревообрабатывающая |
Металлопрокатная |
Фармацевтическая |
Плотники |
Металлурги |
Фармацевты |
|
1 |
1000 |
1000 |
1000 |
100 |
100 |
100 |
|
2 |
100 |
100 |
100 |
10 |
10 |
10 |
|
3 |
100 |
100 |
100 |
10 |
10 |
10 |
|
4 |
100 |
100 |
100 |
10 |
10 |
10 |
|
5 |
100 |
100 |
100 |
10 |
10 |
10 |
|
6 |
100 |
100 |
100 |
10 |
10 |
10 |
Соответственно, первое распределение – самое оптимальное распределение, при котором организации получат выигрыши в размере 1000, а трудовые ресурсы получат выигрыши в размере 100. Данное распределение является равновесным по Нэшу. При данном распределении менять свою стратегию невыгодно ни одному участнику. Если две или все три организации поменяются трудовыми ресурсами, то у данных организаций выигрыши будут составлять в размере 100 вместо 1000, а трудовые ресурсы, поменявшиеся организациями, вместо выигрыша в 100 получат выигрыш в размере 10.
Выводы
Следовательно, в условиях существующих уровней определенности информации о рассматриваемом объекте для построения математической модели социально-экономической системы каждого из изучаемых показателей требуется специальный инструментарий моделирования. В данной работе предлагается способ нахождения компромиссного распределения трудовых ресурсов по организациям. Разработанный способ позволит определять оптимальную стратегию распределения организаций и трудовых ресурсов.



