Охлаждение оборотной воды при непосредственном контакте с воздухом организуется в противоточных, вихревых, с перекрестным током, брызгальных и комбинированных градирнях. Эффективность процесса в градирне, как и в любом другом тепломассообменном аппарате большого размера, зависит от равномерности распределения воды и воздуха в рабочем объеме, где происходит контакт фаз [1–3].
Наиболее эффективным является режим с идеальным вытеснением фаз, т.е. без перемешивания сред, без рецикла и байпаса.
При идеальном вытеснении обеспечивается максимальная движущая сила процесса межфазного переноса. В крупномасштабных градирнях, размеры которых могут достигать нескольких десятков метров, неизбежно возникают значительные неравномерности, особенно с боковыми окнами подачи воздуха по периметру градирни. Даже в мини-градирнях, с размерами 2–4 м, неравномерности связаны с характеристиками вентиляторов для подачи воздуха и различным гидравлическим сопротивлением контактных устройств в центре и у стенок аппарата.
Если при предпроектных расчетах не учитывать эти явления, то определение режимных и конструктивных характеристик может быть выполнено с большой погрешностью, как правило, завышающей тепловую эффективность по сравнению с реальной. Это приводит к недостаточному охлаждению воды и нарушению технологического режима работы установок на ТЭС и различных промышленных предприятий ТЭК и нефтехимии [4–6].
Цель данной работы – представить математическую модель процесса тепло- и массообмена в противоточной пленочной градирне с учетом возможных неравномерностей распределения потоков воды и воздуха. Дать результаты расчетов.
Материалы и методы исследования
Системы уравнений тепло- и массопереноса основываются на уравнениях однофазной гидродинамики и тепломассообмена. Точных решений уравнений переноса для двухфазных сред нет и всегда применяются различные допущения.
Один из подходов заключается в том, что когда дифференциальные уравнения тепло- и массопереноса записываются для каждой фазы отдельно с граничными условиями четвертого рода на межфазной поверхности [7]. При этом предполагается, что площадь межфазной поверхности известна, как и расположение границы раздела фаз в пространстве.
Этот подход применяется для пленочных аппаратов с прямыми каналами (трубками). В градирнях чаще применяются контактные устройства (их в энергетике называют блоками оросителей) более сложной геометрии, т.е. с волнистой поверхностью (гофрами), просечками, криволинейными каналами и т.д.
Таким образом, прямое численное решение системы уравнений с частными производными, записанными раздельно для каждой фазы, затруднительно.
В таких случаях применяются модели с определением межфазных потоков по локальному объему, что значительно упрощает их решение. Используется понятие объемных межфазных источников, которые связаны с коэффициентами переноса и движущими силами процессов. Дальнейшее упрощение подхода к моделированию связано с использованием моделей структуры потоков: диффузионной, ячеечной, а также комбинированных. Однако необходимы экспериментальные исследования аппаратов и определение основных параметров моделей. Таким образом различные упрощения и допущения компенсируются экспериментальной информацией об объекте моделирования и обеспечивается приемлемая точность расчетов.
Далее рассматривается ячеечная модель структуры потоков в контактных устройствах градирен, записанная как при равномерной подаче воды и воздуха, так и при неравномерных профилях скоростей.
При записи уравнений ячеечной модели рабочая зона условно делится на ряд ячеек полного перемешивания. Число ячеек находится экспериментально и косвенно учитывает обратное перемешивание потоков, которое снижает движущую силу процессов и эффективность процесса.
Первоначально рассмотрена равномерная подача воды и воздуха (рис. 1) с применением ячеечной модели для расчета тепловой эффективности.
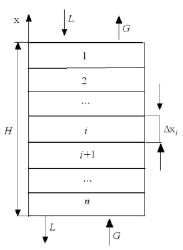
Рис. 1. Условное деление блока оросителей по высоте на ячейки
Выражение ячеечной модели для теплообмена в жидкой фазе
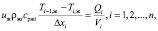(1)
где uж – средняя расходная скорость жидкости на все поперечное сечение блока оросителей, м/с;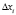 
– высота ячейки, м; Qi – поток тепла в ячейке, Вт; Т – температура, К; Vi – объем ячейки, м3; ρж – плотность жидкости, кг/м3; cрж – удельная теплоемкость, Дж/(кгК); n – число ячеек.
Умножая левую и правую части выражения (1) на площадь поперечного сечения S блока оросителей, получим
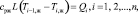(2)
где L – массовый расход воды, кг/с.
Аналогично записываются уравнения теплопереноса в газовой фазе и массопереноса испарившейся воды
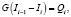(3)
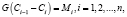(4)
где G – массовый расход воздуха, кг/с; I – энтальпия влажного воздуха, Дж/кг; Mi – поток массы испарившейся влаги, кг/с; С – влагосодержание воздуха, кг/кг.
Поток тепла в ячейке
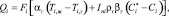
i = 1, 2,..., n, (5)
где Fi – площадь поверхности контакта воды и воздуха в i-й ячейке, м2; αг – коэффициент теплоотдачи, Вт/(м2К); βг – коэффициент массоотдачи, м/с; Ini – энтальпия водяного пара при температуре воды Ti,ж, Дж/кг;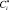 
– влагосодержание насыщенного воздуха, кг/кг. В выражении (4) Mi = Fiβгρг(Сi* – Ci), кг/с.
На основе применения аналогии Льюиса, как показано в работах [4, 5], выражение для потока тепла можно записать в форме
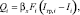(6)
где Iгр,i – значение энтальпии на границе раздела фаз, Дж/кг; βx – коэффициент массоотдачи, кг/(м2с).
Поверхность контакта фаз в i-й ячейке
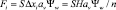, (7)
где Н – высота блоков оросителей, м; аv – удельная поверхность, м2/м3; Ψw – коэффициент смачиваемости насадки.
Коэффициенты тепло- и массоотдачи в хаотичных насадках (блоках оросителей) можно вычислить по выражениям, полученным в результате модификации гидродинамической аналогии (40 < Reэ < 8000) [8]
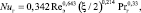(8)
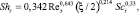(9)
где Nuг = αгdэ/λг – число Нуссельта; Shг = βгdэ/Dг – число Шервуда; Prг, Scг – числа Прандтля и Шмидта. λг, Dг – коэффициенты теплопроводности и диффузии. Для воздуха Prг ≈ Scг ≈ 0,7; ξ – коэффициент гидравлического сопротивления насадки.
Для регулярных насадок (Reг > 3000) [8]
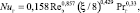(10)
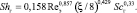(11)
Данные выражения связывают коэффициенты переноса с гидравлическим сопротивлением блока оросителей (коэффициентом ξ), что дает возможность делать расчеты по выделенным зонам с различным перепадом давления.
Число ячеек полного перемешивания связано с модифицированным числом Пекле по обратному перемешиванию Pe = wгН/Dп, где Dп – коэффициент обратного перемешивания, м2/с.
Для регулярных насадок можно использовать выражение [8]
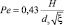(12)
и для хаотичных
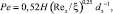(13)
где ξ – коэффициент гидравлического сопротивления; dэ – эквивалентный диаметр насадки, м; Reэ = wгdэ/vг – число Рейнольса; vг – кинематической вязкости газа коэффициент, м2/с; wг – скорость воздуха, м/с.
При известном значении Ре число ячеек можно определить из приближенного соотношения
Pe = 2(n –1). (14)
Таким образом, представленная система уравнений ячеечной модели (2)–(4) является замкнутой.
Из решения системы уравнений (2)–(4) находятся профили температуры воды, энтальпии воздуха и влагосодержание воздуха, что дает возможность вычислить тепловую эффективность охлаждения воды в виде отношения
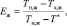(15)
где Tн,ж, Тк,ж – начальная и конечная температура воды, °С; Т* – температура воздуха по смоченному термометру, °С (теоретический предел охлаждения).
На рис. 2 даны результаты расчетов и сравнение с экспериментальными данными для макета градирни с высотой насадки Н = 0,4 м. Температура воды на входе Tн,ж = 32 °С; температура воздуха Tн,г = 25 °С.
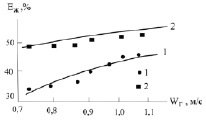
Рис. 2. Зависимость тепловой эффективности охлаждения воды (15) от скорости воздуха на макете градирни с полиэтиленовыми сетчатыми насадками (av ≈ 140 м2/м3); 1 – расход воды 7,61 м3/(м2час); 2 – 4,9 м3/(м2час); точки эксперимент [6, 8]; линии – расчет
Получено удовлетворительное согласование расчетных и экспериментальных результатов по тепловой эффективности охлаждения воды.
В работах В.В. Кафарова, В.В. Шестопалова, Ю.А. Комиссарова и др. показано, что не всегда структуру потоков в аппаратах можно описывать только одномерными моделями. В таких случаях рекомендовано использовать комбинированные модели. Двумерную модель градирни с ячейками полного перемешивания в продольном и поперечном направлениях представим на рис. 3.
Допустим первоначальное равномерное распределение воды (это обеспечивается при числе точек орошения более 50 на м2) и неравномерную подачу воздуха из-за боковой подачи в градирню. В таком случае скорость воздуха будет больше у стенок и меньше в центре [4–6].
Модель для расчета профиля скорости воздуха в нижнем поперечном сечении градирни дана в работах [8, 9]. Далее на основе представленной ячеечной модели (рис. 3) показано влияние неравномерностей на тепловую эффективность градирни. Уравнения ячеечной (2)–(4) записываются для выделенных ячеек, как по высоте, так и в поперечном направлении блока оросителей. Фактически аппарат представляется в виде независимых параллельных зон, в каждой зоне – ячеечная модель по высоте, различное гидравлическое сопротивление, коэффициенты тепло- и массоотдачи и число ячеек, связанные со скоростью воздуха в зоне.
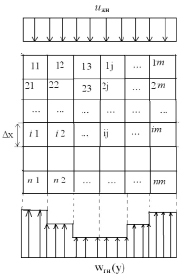
Рис. 3. Условное деление блока оросителей на ячейки при неравномерной подаче воздуха на входе
Результаты исследования и их обсуждение
В результате расчетов установлено, что при равномерном орошении насадки из-за неравномерности подачи воздуха снижение теплового КПД (15) может составлять на 5–15 %.
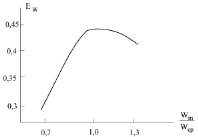
Рис. 4. Зависимость тепловой эффективности от неравномерности распределения воздуха и воды по зонам. Расход в центре 15 м3/м2 час, в зонах у стенки q = 5 м3/м2 час. Насадка аv = 75 м2/м3, высота блоков насадки Н = 1,5 м
На рис. 4 представлены результаты расчетов эффективности (15) по зонам градирни при неравномерности подачи воды и профиля скорости воздуха Wm/Wср, где Wm – скорость воздуха в m – зоне; Wср – средняя скорость на все сечение градирни. Из рис. 4 видно, что наименьшее значение эффективности при Wm/Wср < 1, т.е. в зонах с пониженной скоростью воздуха. Расчеты показывают, что при равномерной подаче фаз (q = 10 м3/ м2час, Wг = 1,5 м/с) значение Еж = 0,44. При наличии неравномерностей осредненное КПД для всей градирни составляет Еж = 0,342, т.е. снижается почти на 30 % относительных.
Расчет средней эффективности (15) при наличии неравномерностей выполняется с осредненной температурой воды на выходе по формуле
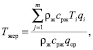(16)
где qi – расход воды в i-й зоне, м3/с, qср – средний расход во всей градирне, м3/с.
Полученные результаты по влиянию неравномерностей распределения фаз на эффективность процесса согласуются с данными работы насадочных колонн при масштабном переходе [10–13].
Выводы
В результате применения ячеечной модели структуры потоков, записанной в вертикальном и поперечном направлениях пленочного блока оросителей градирни, показана возможность учета неравномерностей распределения воды и воздуха в поперечном сечении аппарата. Установлено снижение эффективности охлаждения воды при усилении неравномерностей. Представленная математическая модель может быть обобщена на широкий класс тепло- и массообменных аппаратов при диагностике эффективности процессов и проектировании новых контактных устройств.
Работа выполнена в рамках научного проекта РНФ 18-79-10136 «Теоретические методы моделирования и разработки эффективных импортозамещающих аппаратов очистки и глубокой переработки углеводородного сырья на предприятиях топливно-энергетического комплекса».