На сегодняшний день проблемы экономного использования топливно-энергетических ресурсов (ТЭР) являются приоритетными для предприятий и, как следствие, для государств. Рост стоимости энергоресурсов для предприятий является причиной снижения конкурентоспособности их продукции по причине высокой доли энергозатрат в структуре себестоимости [1]. Конкурентоспособность – это свойство товара, позволяющее удовлетворить запрос покупателя в сравнении с товарами-аналогами. Оценка конкурентоспособности базируется на маркетинговых исследованиях потребностей покупателей в данном товаре на рынке. При выборе потребитель обращает свое внимание в первую очередь на набор качественных параметров.
Основная часть применяемых предприятиями энергоресурсов является невосполняемой, а применение возобновляемых источников энергии является крайне дорогостоящим процессом. Однако для поддержания высокого уровня конкурентоспособности предприятиям необходимо инвестировать в проекты по модернизации оборудования, внедрять современные энергосберегающие технологии. Эффективность использования ТЭР достигается за счет различных способов. Один из таких способов – это формирование портфеля проектов энергомодернизации – процесса повышения энергоэффективности предприятия [2]. При формировании портфеля проектов для предприятий требуется оценка ключевых параметров рекомендуемых мероприятий, т.е. требуемых затрат на реализацию, экономической эффективности от реализации, сроков окупаемости вложенных затрат и т.д.
С учетом вышеизложенного одним из ключевых направлений деятельности предприятия в рамках повышения своей конкурентоспособности является увеличение эффективности использования энергоресурсов.
Цель исследования: создание модели оптимизации портфеля проектов энергомодернизации предприятия с учётом конкурентоспособности.
Материалы и методы исследования
В ходе исследования были проанализированы существующие модели конкурентоспособности, методы формирования портфелей проектов и их оптимизации. В работе были использованы методы системного подхода, сравнительный анализ, моделирование.
Результаты исследования и их обсуждение
Рассмотрим следующую модель конкурентоспособности товара, которая имеет вид
Kтов = (ΠΠ)α (ΠС)β, (1)
где ΠΠ – потребительная предпочтительность, ΠС – стоимостная предпочтительность, a – коэффициент относительной значимости потребительных свойств; b – коэффициент относительной значимости стоимости, α + β = 1.
Модель (1) есть мультипликативная функция ключевых факторов конкурентоспособности товара, исследованная [3] в следующей обобщенной форме:
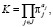
где πj – частный относительный (нормализованный) показатель предпочтительности товара по сравнению с некоторым конкурентом по j-му признаку, aj – коэффициент относительной значимости j-го признака для потребителя. Эта модель является развитием пионерской идеи Джона Нэша применительно к проблеме сравнительного анализа конкурентных преимуществ экономических агентов на основе комплексного критерия.
Для получения факторной модели конкурентоспособности на основе формулы (1) рассмотрим потребительскую предпочтительность оцениваемого товара относительно i-го конкурента:
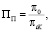
где π0, πiK – качественные потребительные параметры товара и i-го конкурента.
Также рассмотрим стоимостную предпочтительность, включающую в себя предпочтительность по цене приобретения:
,
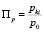и предпочтительность по эксплуатационным затратам:
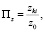
где р0, рki – цены оцениваемого товара и i-го конкурента, z0, zki – затраты на эксплуатацию оцениваемого товара и i-го конкурента за равные периоды.
Следующим шагом введем мультипликативную модель стоимостной предпочтительности в виде среднегеометрического взвешенного соотношения:
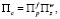(2)
где f – коэффициент относительной значимости цены товара к суммарным расходам на его приобретение и содержание, w – коэффициент относительной значимости расходов на содержание товара к суммарным расходам на его приобретение и содержание.
Подставив Πz и Πp в модель (2), получаем
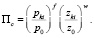(2а)
Исходя из этого модель (1) для уровня конкурентоспособности (количественной оценки конкурентоспособности) примет вид
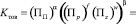
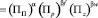, (3)
или как мультипликативная факторная модель конкурентоспособности j-го товара относительно i-го конкурента:
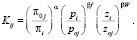(4)
Модель (4) дает количественную оценку привлекательности товара для потребителя по отношению к конкурирующему товару, обладающему схожими характеристиками.
Введем аддитивную взвешенную модель конкурентоспособности предприятия KΣ как интегральный показатель конкурентоспособности его товаров:
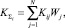(5)
где Wj, j∈N – вектор коэффициентов значимости товаров предприятия в формировании его конкурентоспособности.
Модель (5) основана на принципе агрегирования частных критериев конкурентоспособности товаров в виде обобщенного критерия конкурентоспособности предприятия и базируется на теории максимизации ожидаемой полезности Д. Неймана и О. Моргенштерна. Современную форму такого подхода [4] представляет совокупная полезность, которая определяется как взвешенная сумма (агрегированный критерий) частных полезностей:
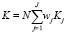
при
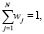
где wj – весовые коэффициенты критериев (0 < wj < 1), определяемые различными способами: отношений, компенсации, цены критериев, взвешенной полезности.
Сформулируем методологию формирования функциональной зависимости конкурентоспособности товара (4) от издержек на ТЭР, расходуемых при его производстве.
Известно, что цена предложения товара есть функция предельных издержек (MCj) на возрастающем участке выше уровня средних издержек, то есть
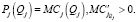(6)
Представим предельные издержки как сумму двух компонентов (рис. 1). Энергозатраты на производство единицы товара еj и прочие (кроме энергозатрат) издержки на производство единицы товара Сj:
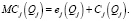(7)
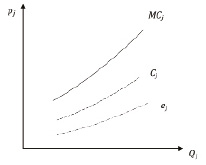
Рис. 1. Декомпозиция функции предельных издержек
Введем следующую функцию энергозатрат (рис. 2), удовлетворяющую условию (6):
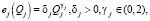(8)
где δj, γj – параметры функции энергозатрат, определяющие энергоэффективность производства j-го товара; δj – удельные (средние) энергозатраты на единицу продукции; γj – темп роста энергозатрат в процентах, с увеличением объема производства на 1 %.
Функция энергозатрат (8) соответствует форме классической функции долгосрочных издержек предприятия
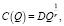
где r – коэффициент эффекта расширения масштаба, D – средние издержки предприятия.
Проведя подстановку формул (7) и (8) в формулу (6)
,
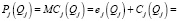
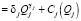получим модель зависимости цены предложения j-го товара предприятия от параметров энергоэффективности:
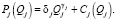(9)
Полученную модель подставим в модель (4):
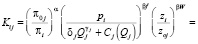
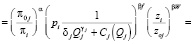
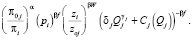
В результате этого получаем зависимость конкурентоспособности j-го товара относительно i-го конкурента от параметров энергоэффективности:
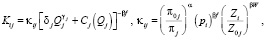(10)
где коэффициент κij характеризует компоненты конкурентоспособности товара, не зависящие от энергоэффективности.
Подставим (10) в аддитивную взвешенную модель конкурентоспособности (5), в результате чего получим концептуальную факторную модель зависимости конкурентоспособности предприятия от параметров энергоэффективности его технологии:
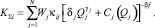(11)
Модель позволяет найти оптимальные параметры δj, γj, j∈N из условия max KΣi при заданной производственной программе Qj = const.
Продифференцируем функцию конкурентоспособности предприятия (11) по параметрам энергоэффективности δj и γj:
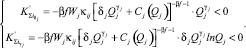(12)
Производные будут иметь отрицательные значения, так как коэффициенты (β, f, Wj, κij) положительны, но знак минус дает отрицательность всей производной.
Анализ (12) показывает, что уменьшение параметров энергоэффективности δj, γj приводит к росту конкурентоспособности, поскольку этот эффект получается за счет отрицательной степени –βf выражения в функциях издержек в формуле конкурентоспособности (11). Аналогичное происходит и с увеличением общих издержек Cj(Qj), а увеличение значения коэффициента κij, характеризующего компоненты конкурентоспособности товара, не зависящие от энергоэффективности, приводит к росту конкурентоспособности.
Формирование факторной модели конкурентоспособности предприятия базируется [5] на модели мультиагентной системы.
Обобщенная модель системы включает в себя следующие компоненты:
- взаимодействующие подсистемы, общее число которых K, а соответствующей подсистеме присвоен индекс k = 1,…, K;
- взаимодействующие агенты (обозначены символом А), интегрированные в подсистемы, число которых в k-й подсистеме равно Nk, а соответствующему агенту присвоен индекс n = 1, 2,…, Nk.
Использованы множества индексов K = {k = 1, 2,…, K}, Nk = {n = 1, 2,…, Nk}, индекс k = 0, n = 0 соответствует метацентру.
Цель функционирования системы – максимизация векторного критерия, компонентами которого служат частные критерии эффективности:
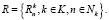
На основе этой обобщенной модели разработана модель зависимости конкурентоспособности предприятия (рис. 2) как иерархическая система взаимосвязей:
а) параметры энергоэффективности влияют на энергозатраты;
б) энергозатраты влияют на конкурентоспособность товара;
в) конкурентоспособность товара формирует конкурентоспособность предприятия.
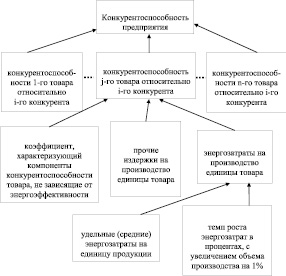
Рис. 2. Факторная модель конкурентоспособности предприятий
Пусть проекты энергомодернизации дифференцированы по товарам, производимым предприятием, то есть каждый товар выпускается по обособленной технологии.
Определение: проектом энергомодернизации называется комплекс мероприятий, результатом которых является некоторое значение параметров энергоэффективности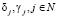 
. Поэтому проект однозначно характеризуется вектором:
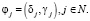(13)
Определение: портфелем Ф проектов энергомодернизации называется комплекс взаимосвязанных по срокам осуществления и объектам реализации проектов энергомодернизации.
В свою очередь портфель проектов энергомодернизации предприятия задается в векторном виде
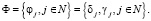
Однако не все функции энергозатрат, удовлетворяющие ограничению (8), допустимы, поскольку в случае нулевых значений коэффициентов функции энергозатрат эта функция равна нулю, что экономически означает закрытие производства по j-й технологии.
Поэтому введем допустимое множество проектов энергомодернизаций в виде
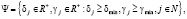(14)
где δmin, γmin – минимальные значения коэффициентов функции энергозатрат, при которых обеспечивается требуемый уровень объема производства.
В задачах многокритериальной оптимизации критерии могут нести в себе различные экономические смыслы, могут быть выражены в разных единицах измерения, что делает сравнение критериев по численному значению невозможным, а это в свою очередь затрудняет применение всех методик многокритериальной оптимизации. В связи с этим поиск решения многокритериальной задачи требует введения предварительного этапа – нормализации критериев. В исследованиях [6] Ю.К. Машунина нормализация критериев представляет собой однозначное отображение функции fk(X), ∀k∈K, из RN в RN.
Таким образом, анализ теоретических основ нормализации приводит к выводу об удобстве применения модели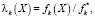 
.
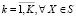На основании данной теории комплексную оценку проекта, интегрирующую двухпараметрическую модель (13), предлагается осуществлять по следующей взвешенной нормализованной модели:
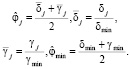(15)
Вектор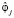 
представляет собой комплексную оценку энергоемкости технологии и является параметром управления при выборе проекта энергомодернизации.
Модель оценки энергоемкости технологии (15) сводит задачу выбора проекта энергомодернизации к однопараметрическому виду. Поскольку оценки проектов (15) выражены в безразмерной и нормализованной форме, то есть инвариантны относительно линейного преобразования, то допустимо ввести линейную функцию инвестиционных затрат на проведение типового проекта энергомодернизации в виде
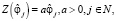(16)
где α – обобщенный коэффициент затратоёмкости проектов энергомодернизации предприятия, рассчитанный по ретроспективному периоду методами регрессионного анализа.
Для определения коэффициентов регрессии методом наименьших квадратов, например, для уравнения y = at + b, составляется сумма квадратов отклонений как функция неизвестных параметров a, b.
Сформулируем задачу формирования оптимального инвестиционного портфеля.
Теоретические основы формирования портфелей заложены в ряде научных теорий [7], базирующихся на методах проектного анализа [8] и механизмах распределения ресурсов [9].
Базовая модель распределения ресурсов [10] следующая: объем ресурса IR распределяется между N проектами в виде вектора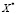 
по следующим условиям:
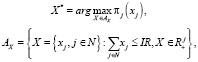
где πj (xj), j∈N – функции полезности агентов.
Руководствуясь основами данных теорий, введём ограничение на объем инвестиций IR, направляемых в данном периоде на все проекты энергомодернизации. Таким образом, модель выбора портфеля проектов энергомодернизации предприятия, оптимизирующего его конкурентоспособность, имеет вид
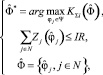(17)
где символом * обозначается оптимальное значение портфеля.
Заключение
Решением модели является вектор оценок допустимых по технологическим и финансовым ограничениям проектов, который по экономическому смыслу выражает вектор приоритетности проектов, включенных в портфель.
Таким образом, в результате исследования была получена модель, позволяющая оптимизировать портфель проектов энергомодернизации предприятия и выбрать проекты, повышающие конкурентоспособность.