В макроэкономической теории рассматриваются волновые явления в экономике, когда под действием каких-то факторов происходит отклонение макроэкономических показателей от их устойчивого состояния или от их траектории движения [1–2]. Среди таких показателей особое место занимает национальный доход, являющийся одним из обобщающих показателей экономического развития страны. Волновой характер изменения экономики в зависимости от времени является формой прогрессивного развития рыночной экономики. При этом каждая волна характеризует целый цикл экономического развития [3–5]. Отметим, что в основе теории экономического цикла лежит выяснение причин колебаний экономической активности общества во времени. Отметим также, что так как цикличность прямым или косвенным образом действует на рыночную экономику, то она является важной макроэкономической проблемой.
При построении динамической модели волнового изменения национального дохода можно пользоваться различными математическими моделями, описывающимися при помощи обыкновенных дифференциальных уравнений [6].
Цель исследования: найти зависимость национального дохода от времени в рамках модели гармонического осциллятора и провести многосторонний анализ полученного результата.
Постановка задачи, метод решения и результаты исследования
Пусть национальный доход Y(t) как функция от времени t удовлетворяет обыкновенному однородному дифференциальному уравнению второго порядка с постоянными действительными коэффициентами (модель гармонического осциллятора)
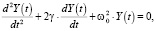(1)
где первый член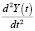 
показывает темп изменения национального дохода (в физике это соответствует ускорению движения), второй член 
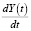связан с транзакционными издержками (издержки на переговоры, на юридическую защиту и т.д.) (в физике это соответствует силе трения), а третий член 
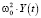есть рыночная сила (в физике это сила, которая возвращает систему к точке равновесия), γ – коэффициент затухания, ω0 – частота свободных колебаний (γ = 0).
Любопытно отметить, что аналогичное дифференциальное уравнение для функции Y(t) можно получить исходя из динамической модели Кейнса [7]. В основе этой модели лежит основной закон экономического баланса, который имеет вид
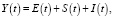(2)
где Y(t) – национальный доход, E(t) – расходы, S(t) – национальное потребление, I(t) – инвестиции. Представляя функцию потребления в виде суммы
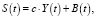(3)
где B(t) – конечное потребление, 0 < c < 1 – постоянный коэффициент, и учитывая, что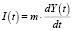 
(m = const), а функции E(t) и B(t) известны, из (2) относительно функции Y(t) получим следующее обыкновенное дифференциальное уравнение первого порядка
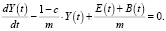(4)
Дифференцируя обе части уравнения (4) по t и предполагая, что
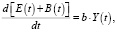
где b – постоянный коэффициент, получим
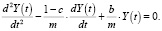(5)
Сравнивая (5) с (1), можно сказать, что национальный доход Y(t) описывается дифференциальным уравнением гармонического осциллятора с частотой свободных колебаний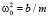 
и коэффициентом затухания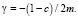 
Решение линейного однородного дифференциального уравнения (1) будем искать методом Эйлера, а именно в виде [8]
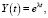(6)
где λ – пока неизвестные числа (действительные, комплексные или чисто мнимые). Подставляя (6) в (1) для определения характеристических чисел, получим следующее квадратное уравнение
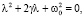(7)
решения которого имеют вид
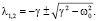(8)
Из (8) видно, что характер решений уравнения (7) зависит от знака выражения под квадратным корнем. Рассмотрим случаи:
1. 
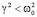(коэффициент затухания меньше частоты свободных колебаний).
Очевидно, что в этом случае имеем комплексные корни характеристического уравнения (3) в виде
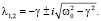(9)
Тогда линейно независимые решения дифференциального уравнения (1) имеют вид
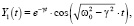
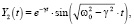(10)
а общее решение, как суперпозиция независимых решений, запишется в виде
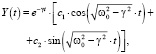(11)
где c1 и c2 – произвольные постоянные. Нетрудно заметить, что (11) можно представить в виде
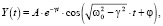(12)
где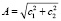 
– амплитуда колебаний, 
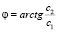– начальная фаза. Выражение (8) показывает, что при γ < ω0 и γ > 0 национальный доход в зависимости от времени имеет колебательный характер с резко выраженными максимумами и минимумами. График зависимости национального дохода от времени приведен на рис. 1. Кривые построены согласно формуле 2,5 + Y(t) при изменении t от 0 до 24 (t измеряется в месяцах) и при следующих значениях параметров, характеризующих рассматриваемый процесс: c1 = c2 = 1, ω0 = 1, γ = 0,07; 0,08; 0,1.
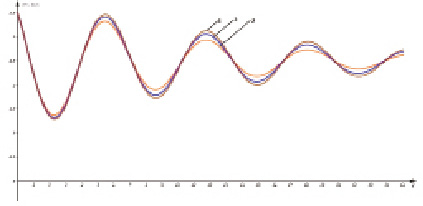
Рис. 1. Зависимость функции 2,5 + Y(t) от времени t при ω0 = γ:1 – ω0 = 1, γ = 0,07; 2 – ω0 = 1, γ = 0,08; 3 – ω0 = 1, γ = 0,1
Полученные кривые показывают, что огибающие максимумов с возрастанием времени убывают по экспоненциальному закону и при t→∞ стремятся к нулю. Из рис. 1 также следует, что с увеличением коэффициента затухания γ при фиксированном значении частоты собственных колебаний ω0 значения максимумов уменьшаются.
2. 
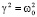или γкр. > ω0 (затухание критическое, так как при γ > ω0 осциллятор будет совершать колебательное движение).
В этом случае характеристическим числам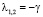 
соответствуют два независимых решения
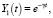
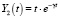. (13)
И общее решение дифференциального уравнения (1) представится в виде
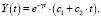(14)
Из (14) следует, что процесс имеет неколебательный характер, и так как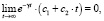 
то осциллятор экспоненциально будет стремиться к положению равновесия. На рис. 2 приведены графики зависимости национального дохода Y как функция от времени t, построенные согласно формуле (14) при следующих значениях параметров: c1 = c2 = 1, ω0 = γ = 0,07; 0,08; 0,1 и 0 ≤ t ≤ 24. Кривые показывают убывающий характер национального дохода как функция от времени, причем при увеличении значений ω0 = γ скорость стремления к нулю при возрастании t увеличивается.
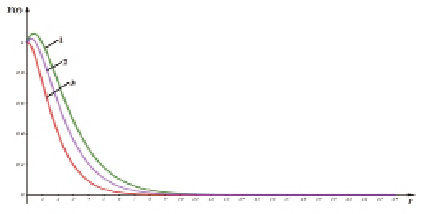
Рис. 2. Зависимость национального дохода Y от времени t при ω0 = γ:1 – ω0 = γ = 0,07; 2 – ω0 = γ = 0,08; 3 – ω0 = γ = 1
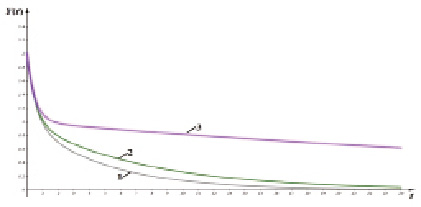
Рис. 3. Зависимость национального дохода Y от времени t при γ > ω0:1 – ω0 = 0,6; γ = 1; 2 – ω0 = 0,5; γ = 1; 3 – ω0 = 0,2; γ = 1
3. γ > ω0 (соответствует большим транзакционным затратам).
В этом случае характеристическое уравнение (3) имеет два различных действительных решения и общее решение дифференциального уравнения (1) будет иметь вид
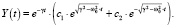(15)
Так как при
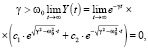
то имеем неколебательный процесс и осциллятор будет стремиться к положению равновесия. Зависимости национального дохода Y от времени t в этом случае приведены на рис. 3.
Как видно из рисунка, национальный доход как функция от времени при γ > ω0 является убывающей функцией, при этом чем больше ω0, тем быстрее функция стремится к нулю при t→∞.
Заключение
В работе с помощью решения линейного однородного обыкновенного дифференциального уравнения с постоянными действительными коэффициентами решена задача динамики изменения национального дохода в зависимости от времени в рамках классической модели гармонического осциллятора. Проведенный графический анализ на основе полученных в работе аналитических выражений для национального дохода в зависимости от времени показывает, что при различных значениях параметров, характеризующих рассматриваемый процесс, изменение национального дохода может иметь волновой или неволновой характер. В случае, когда коэффициент затухания меньше частоты свободных колебаний, национальный доход в зависимости от времени имеет колебательный характер, причем с увеличением времени амплитуда колебаний уменьшается. А когда коэффициент затухания больше или равен частоте свободных колебаний, национальный доход не имеет колебательного характера и стремится к нулю при увеличении времени. Другими словами, в этом случае осциллятор будет экспоненциально стремиться к положению равновесия.