Изучение повышения эффективности технологических процессов при смешении сред представляет большое практическое значение, особенно эта тема актуальна при течении вязких жидкостей. Одним из наиболее эффективных оборудований для перемешивания сред является статический смеситель.
Статические смесители выгодно отличаются от других конструкций отсутствием движущихся элементов. Они сочетают в себе одновременно высокую производительность, низкую энергоемкость, возможность изготовления из самых разнообразных конструкционных материалов (металлов, полимеров, керамики и т.п.), их простота и высокая эффективность стимулируют к созданию все новых конструктивных решений в данной области.
На предприятиях энергетики и нефтехимии статические смесители нашли применение в установках для ввода присадок в топливо, улучшающих его качество, для приготовления смесей, эмульсий, для ввода флокулянтов в суспензии.
К простому типу статических смесителей относится обычный трубопровод (канал). В целях повышения эффективности процесса смешения в смесителях устанавливают различные турбулизирующие вставки (смесительные элементы).
С целью повышения эффективности проведения процесса смешения вязких сред в статье рассматривается применение статических смесителей, в которых в качестве турбулизирующих вставок используются хаотичные насадочные слои. Хаотичный насадочный слой, как один из видов интенсификаторов процесса смешения сред, представляет значительный интерес для создания энергокорректных технологий в современных аппаратах. Тем не менее с применением насадочного слоя в смесителе увеличивается сопротивление потоку, что приводит к дополнительным затратам энергии на преодоление возросшего сопротивления, поэтому целесообразность применения насадочного статического смесителя для смешения вязких сред необходимо определять с помощью энергетической эффективности.
Цель исследования: в качестве примера рассмотрим следующую задачу: рассматривается статический смеситель насадочного типа для ввода присадок в мазут марки М-100, который устанавливается в трубопровод диаметром 200 мм.
Для выбора наиболее энергоэффективного смесителя насадочного типа проведем сравнительную энергетическую оценку статического смесителя, заполненного насадочными слоями различной формы, в зависимости от числа Рейнольдса, а также для оценки влияния размера насадки на эффективность работы смесителя насадочного типа рассмотрим в качестве насадок стальные кольца Палля различного диаметра.
Материалы и методы исследования
Определение энергетического коэффициента
Существует много методов оценки энергетической эффективности тепло- и массообменного оборудования. При оценке тепломассообменных характеристик широкое применение нашел подход с использованием энергетических коэффициентов В.М. Кирпичева и В.М. Антуфьева [1].
На основе выражения В.М. Антуфьева (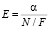
) аналогично получен коэффициент, используемый для выбора энергоэффективных смесителей насадочного типа, и имеет вид [2]
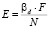, (1)
где βd – коэффициент скорости переноса частиц, м/с; F – площадь насадочного слоя, м2; N – затраченная мощность на перекачивание среды, Вт.
Площадь насадочного слоя находится как [3]
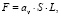(2)
где аν – удельная поверхность насадки, м2/м3; S – площадь поперечного сечения смесителя, м2; L – длина насадочного слоя, м.
Затраченная мощность на перекачивание среды имеет вид 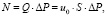[3]
(3)
где Q – расход жидкости, м3/с; ΔP – перепад давления, Па; u0 – скорость среды, м/с.
Потери давления в канале, заполненном хаотичным насадочным слоем, определяются известным выражением 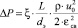[4]
, (4)
где ξ – коэффициент гидравлического сопротивления насадочного слоя; dэ = 4•εсв/аν – эквивалентный диаметр насадки, м; εсв – свободный объем насадки, м3/м3; ρ – плотность среды, кг/м3.
Таким образом, выражение энергетического коэффициента для смесителя примет вид
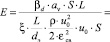
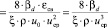, (5)
где uср = u0/εсв – средняя скорость среды в насадке, м/с.
Запишем энергетический коэффициент в безразмерном виде через число Стантона
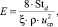(6)
где Std = βd/uср – число Стантона.
Итак, основная задача при определении энергетического коэффициента сводится к нахождению коэффициента скорости переноса частиц βd и коэффициента гидравлического сопротивления насадочного слоя ξ.
Следует отметить, что коэффициент гидравлического сопротивления определяется экспериментально по значениям ΔР на основе выражения (4).
Коэффициенты гидравлического сопротивления насадочного слоя для некоторых видов насадок находятся по следующим известным выражениям [4]:
для кольцевых насадок
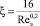, (7)
для шарообразных насадок
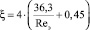, (8)
для седлообразных насадок
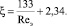(9)
Определение коэффициента скорости переноса частиц
Выражение коэффициента скорости переноса частиц запишем на основе аналогии переноса импульса и массы [2]
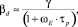(10)
где γ – коэффициент переноса импульса, м/с; ωЕ – угловая частота турбулентных низкочастотных пульсаций, с-1; τр – время релаксации, с.
Тогда сопротивление скорости переносу частиц в пристенном слое с учетом аналогии (10) примет вид [2]
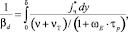(11)
где jч* – относительный поток массы частиц; ν – коэффициент кинематической вязкости, м2/с; νТ – коэффициент кинематической турбулентной вязкости, м2/с.
Характеристики турбулентного обмена запишем на основе трехслойной модели турбулентного пограничного слоя, с учетом затухания турбулентных пульсаций [5]
, где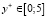 
, (12)
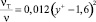, где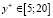 
, (13)
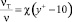, где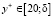 
. (14)
На основе выражения (11), используя трехслойную модель турбулентного пограничного слоя (12)–(14), произведено интегрирование и получен коэффициент скорости переноса частиц [2]
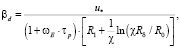(15)
где u* – динамическая скорость, м/с; R1 = 5 – безразмерная толщина вязкого подслоя; Rδ – безразмерная толщина пограничного слоя; R0 – безразмерная толщина вязкого подслоя.
Средняя динамическая скорость на поверхности неупорядоченных насадок определяется как [6]
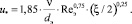(16)
Выражение безразмерной толщины пограничного слоя имеет вид [3]
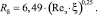(17)
Характеристики пограничного слоя на стенке канала с насадкой находятся из следующих выражений [3]:
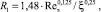(18)
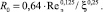(19)
Тогда коэффициент скорости переноса частиц примет вид [2]
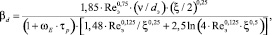(20)
где Reэ = uср•dэ /ν – эквивалентное число Рейнольдса.
Угловая частота турбулентных низкочастотных пульсаций находится из выражения [7]
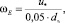(21)
а время релаксации как [7]
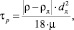(22)
где ρд – плотность дисперсной фазы, кг/м3; dд – диаметр дисперсной фазы, м; μ – коэффициент динамической вязкости, Па·с.
Для насадочного смесителя безразмерный комплекс Стантона с учетом выражений (20)–(22) получит вид
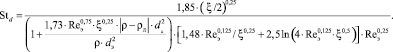(23)
Результаты исследования и их обсуждение
Проведем сравнительную энергетическую оценку статического смесителя, заполненного насадочными слоями различной формы, в зависимости от числа Рейнольдса.
Рассматриваемый диапазон чисел Рейнольдса Reэ = 50÷1000.
Параметры мазута:
температура tм = 80 °С;
плотность ρм = 990 кг/м3;
коэффициент кинематической вязкости ν = 9,5·10-5 м2/с.
Характеристики дисперсной фазы:
dч = 0,09 мм;
ρч = 876 кг/ м3.
В качестве насадок рассматривались три вида хаотичных насадок с близкими номинальными размерами:
1) стальные кольца Палля (разм. 15 мм), с техническими характеристиками: dэ = 0,01 м, аν = 380 м2/м3, ?св = 0,93 м3/м3;
2) шарообразная насадка (разм. 14 мм), с техническими характеристиками: dэ = 0,006 м, а? = 273 м2/м3, ?св = 0,41 м3/м3;
3) седлообразная насадка Инталокс (разм. 12,5 мм), с техническими характеристиками: dэ = 0,005 м, а? = 625 м2/м3, ?св = 0,78 м3/м3.
Для упрощения расчетов вычисления проводились с применением программного обеспечения МathCad 15.
Полученные результаты представлены на рис. 1 в виде зависимости энергетического коэффициента Е от числа Рейнольдса Reэ.
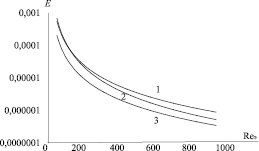
Рис. 1. Зависимость энергетического коэффициента Е от числа Рейнольдса Reэ: 1 – стальные кольца Палля (разм. 15 мм); 2 – стальные шары (разм. 14 мм); 3 – седла Инталокс (12,5 мм)
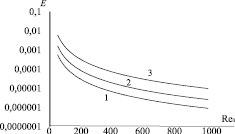
Рис. 2. Зависимость энергетического коэффициента Е от числа Рейнольдса Reэ: 1 – стальные кольца Палля (разм. 15 мм); 2 – стальные кольца Палля (разм. 25 мм); 3 – стальные кольца Палля (разм. 50 мм)
Процесс смешения сред в аппаратах со смесительными элементами (вставками) напрямую связан с гидродинамическими особенностями обтекания элементов структуры насадочного слоя.
Так как насадки имеют разнообразную форму (кольца, шары, седла), то каналы, образованные пустотами в слоях элементов, имеют сложную конфигурацию, благодаря этому поток жидкости, двигаясь через насадочный слой, одновременно обтекает отдельные элементы слоя и движется внутри каналов сложной формы.
Шары имеют правильную геометрическую форму, не имеющую внутренней полости, вследствие чего они имеют низкую пропускную способность, в отличие от двух других форм насадок, что в целом приводит к небольшой энергетической эффективности.
Поверхность седел Инталокс, благодаря своей особенности формы, смачивается лучше, чем поверхности других форм, что приводит к высокой эффективности, однако они имеют достаточно высокие значения коэффициента гидравлического сопротивления, которые в ряде случаев возрастают значительно быстрее, чем значения коэффициента скорости переноса частиц.
Среди рассматриваемых насадок необходимо выделить как наиболее эффективные – кольца Палля, вследствие своих конструктивных особенностей, при их использовании получаем наибольшие значения E энергетического коэффициента.
Далее для оценки влияния размера насадки на эффективность работы смесителя насадочного типа рассмотрим в качестве насадок стальные кольца Палля различного диаметра:
1) стальные кольца Палля (разм. 15 мм), с техническими характеристиками: dэ = 0,01 м, аν = 380 м2/м3, εсв = 0,93 м3/м3;
2) стальные кольца Палля (разм. 25 мм), с техническими характеристиками: dэ = 0,017 м, аν = 220 м2/м3, εсв = 0,92 м3/м3;
3) стальные кольца Палля (разм. 50 мм), с техническими характеристиками: dэ = 0,033 м, аν = 108 м2/м3, εсв = 0,95 м3/м3.
Полученные результаты представлены на рис. 2 в виде зависимости энергетического коэффициента Е от числа Рейнольдса Reэ.
Как показывает график, наибольшие значения энергетического коэффициента Е имеют кольца Палля разм. 50 мм, что связано с их основными характеристиками, они имеют небольшие значения коэффициента гидравлического сопротивления и высокую производительность.
Выводы
С точки зрения интенсификации процесса смешения, при минимальных затратах энергии на преодоление возросшего сопротивления потоку, представляется интересным применение сравнительно крупной насадки.
Во всех рассмотренных случаях с увеличением числа Рейнольдса мощность на прокачивание среды быстро нарастает пропорционально увеличению средней скорости среды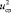 
, и значение коэффициента энергетической эффективности Е снижается.
Данный подход определения энергетической эффективности позволяет вводить наименьшее количество эмпирических параметров и при такой постановке об объекте моделирования достаточно знать эмпирическую информацию значения перепада давления рабочей зоны и определить коэффициент скорости переноса частиц.