В настоящее время существует два основных подхода к моделированию структуры и конечных механических свойств стали после термомеханической обработки. Первый подход применяет полуэмпирические модели, которые определяют связь между внешними параметрами процесса деформации (такими как температура, скорость и степень деформации) и получаемой микроструктурой [1, 2], используя ряд подгоночных параметров. Хотя такой подход относительно прост в реализации, но из-за слабой физической основы даёт неплохие результаты лишь при небольших отклонениях от условий, при которых были получены подгоночные параметры модели.
Во втором подходе для описания процессов, происходящих во время термомеханической обработки, используются не только «внешние» переменные процесса, но и переменные, описывающие внутреннее состояние материала – плотность дислокаций, размер субзёрен и т.п. [3–5]. В моделях такого типа большинство применяемых констант имеет физический смысл, поэтому они являются более перспективными.
Однако существенным недостатком обеих подходов является то, что они либо абсолютно не учитывают влияние ансамбля выделений вторых фаз (в том числе карбонитридных) на эволюцию структуры при термомеханической обработке, либо учитывает её косвенно, либо в лучшем случае на очень упрощённом уровне. Между тем карбонитридобразующие элементы могут оказывать значительное влияние на кинетику рекристаллизации и вносят свой вклад в упрочнение материала по механизму дисперсионного твердения.
В наших предыдущих исследованиях [6, 7] была предложена модель для описания эволюции выделений нескольких составов на всех стадиях процесса, начиная с зарождения и заканчивая коагуляцией. В работе [7] были совместно использованы эта модель [6] и деформационная модель для описания изменения размера зерна аустенита сталей, микролегированных сильными карбонитридообразующими элементами, при горячей деформации в температурном диапазоне стабильного аустенита. Однако этот подход, позволяющий прогнозировать эволюцию выделений при горячей деформации, не был подробно разобран и протестирован. Это является целью настоящей работы.
Модель
Для моделирования процессов, протекающих при деформации и после нее, в нашем подходе учитывается взаимное влияние плотности дислокаций в материале, среднего размера аустенитного зерна и характеристик ансамбля карбонитридных выделений.
Для описания эволюции плотности дислокаций в материале рассчитывается изменение средней плотности дислокаций в сплаве 
, которая связана с плотностью дислокаций в деформированных и рекристаллизованных зёрнах, ρ0, соотношением
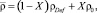(1)
где X – доля материала, претерпевшего рекристаллизацию.
При этом использовалось модельное допущение о том, что ρDef одинакова во всех деформированных зёрнах, а ρ0 полагалась постоянной величиной. Таким образом, изменение средней плотности дислокаций в материале можно записать как
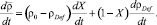(2)
Здесь t – время, а dX/dt – скорость рекристаллизации.
Для вычисления ρDef в процессе деформации был использован подход, предложенный в работе [3]. При этом было использовано допущение, что статические и динамические процессы возврата и рекристаллизации описываются одинаковыми выражениями.
Выражение для изменения плотности дислокаций в деформированном материале имеет вид [4]:
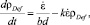(3)
где 
– скорость деформации, b – вектор Бюргерса, d – длина свободного пробега дислокации, k – коэффициент динамического возврата, t – время.
Согласно [8] доля материала, претерпевшего рекристаллизацию, как функция скорости миграции границ зерен vb и скорости образования зародышей рекристаллизации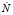 
, может быть представлена в виде
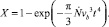(4)
Чтобы учесть влияние выделений вторых фаз при описании скорости миграции границы зерна, рассматривается суперпозиция сил, действующих на границу зерна аустенита. В этом случае скорость миграции границы описывается выражением [8]:
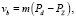(5)
где m – подвижность границ зерен, Pd – движущая сила роста зерна, которая задается как давление на единицу площади границы зерна; PZ – тормозящая сила, препятствующая миграции и действующая со стороны частиц.
Скорость зарождения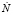 
новых зёрен для динамической рекристаллизации рассчитывалась по формуле [8]:
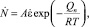(6)
где A – константа, зависящая от температуры, Qn – энергия активации образования зародышей, Т – абсолютная температура, R – универсальная газовая постоянная. Согласно [8] Qn = 260 кДж/моль. В работе [8] были определены значения A для трех температур. Обработка этих результатов позволила получить следующее выражение для температурной зависимости A:
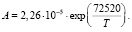(7)
Выражение (6) описывает скорость зарождения только при динамической рекристаллизации. Образованием новых зародышей при статической рекристаллизации в данной работе мы пренебрегали. Это допущение не должно вносить существенной погрешности, если уже прошла динамическая рекристаллизация.
Подвижность высокоугловых границ зерен m зависит от температуры и может быть описана аррениусовской зависимостью 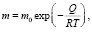[8]:
(8)
где m0 – предэкспоненциальный множитель; Q – энергия активации движения границы. Согласно [8] m0 = 120 м4/(Дж·с), Q = 310 кДж/моль.
Рост рекристаллизованных зерен зависит от разности плотностей дислокаций в рекристаллизованных, ρRex, и деформированных зернах, ρDef, таким образом, движущая сила может быть определена как
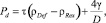(9)
где γ – удельная энергия границы зерна, равная 0,5 Дж/м2 [8], а τ = Gb2/2 – энергия дислокации, приходящаяся на единицу ее длины.
Плотность дислокаций в рекристаллизованных зернах предполагалась равной равновесной плотности дислокаций для заданной температуры, которая рассчитывалась как [9]:
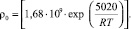(11)
Дисперсные частицы тормозят движение границы зерна. Тормозящая сила PZ, действующая со стороны сферических частиц, распределенных случайным образом в матрице, выражается как [10]:
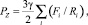(12)
где Fi – объемная доля, приходящаяся на частицы со средним радиусом Ri из i-го размерного интервала. Критическая плотность дислокаций, необходимая для начала рекристаллизации, согласно работе [11], определяется как
(13)
Более подробное описание той части нашей модели, которая касается изменения среднего размера зерна и плотности дислокаций в материале, дано в работе [7].
Для расчета скорости рекристаллизации необходимы данные о характеристиках ансамбля выделений вторых фаз – их объемных долях и распределении по размерам. Эту информацию обеспечивает кинетическая часть модели [6]. Входными данными для неё являются составы сплава и карбонитридных фаз, а также объемные доли выделений и распределения частиц по размерам в текущий момент времени для каждой фазы. Кроме того, в качестве входного параметра здесь используется средняя плотность дислокаций в образце,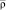 
, которая необходима для расчёта скорости зарождения новых выделений. На основании этих параметров прогнозируется последующее изменение объёмных долей и распределение по размерам карбонитридных частиц. Более подробно кинетическая модель описана в работе [6].
Выбор исходных данных для моделирования
Для оценки возможностей прогнозирования размера карбонитридных выделений в сталях, подвергаемых деформации в аустенитной области, с помощью предложенного алгоритма было выполнено сравнение результатов расчетов с экспериментальными данными, взятыми из работы [12]. В этой работе c помощью методики углеродных реплик и просвечивающей электронной микроскопии получали информацию о составе и морфологии частиц, характере их распределения в образце и среднем размере выделений после нескольких термомеханических обработок низколегированной стали. Исследования были выполнены на углеродистой низколегированной стали с Ti и Nb, химический состав которой приведен в таблице.
Состав исследуемой стали, мас. % [12]
|
C |
Cr |
Ti |
Nb |
N |
Ni |
|
0,16 |
1,64 |
0,002 |
0,031 |
0,012 |
1,56 |
Образцы, вырезанные из промышленной заготовки, сначала подвергались выдержке при 1250 °C в течение 600 с, затем часть образцов закаливали и изучали фазовый состав и размер карбонитридных частиц. Остальные образцы охлаждали со скоростью 200 °C в минуту до температуры деформации в 900 °C. Затем часть образцов подвергали деформации со скоростью 1 с–1 , а часть со скоростью 0,001 с–1 до достижения степени деформации 1, после чего шла изотермическая выдержка при температуре деформации. Продолжительность цикла, включающего деформацию образцов с заданной скоростью и последующую изотермическую выдержку при температуре деформации, составляла 1025 с для обеих обработок. Затем образцы закалялись, после чего также изучалось состояние ансамбля карбонитридных частиц.
В качестве исходного состояния для моделирования мы брали состояние образца после аустенизации при 1250 °C. Авторы работы [12] сообщают, что в данной стали после выдержки в течение 600 с при температуре 1250 °C обнаруживаются богатые титаном частицы со средним размером 22 нм. После цикла, включающего деформацию со скоростью 1 с–1 и отжиг, в стали присутствуют выделения, большая часть которых близка по составу к карбонитриду ниобия, со средним радиусом 5 нм. После такого же цикла, но с меньшей скоростью деформации в 0,001 с–1 в стали присутствуют частицы со средним радиусом 3,5 нм, подавляющее большинство которых близко по составу к карбонитриду ниобия.
Объемные доли выделений не измерялись в [12]. Они были оценены нами с помощью программы IMP Equilibrium, предназначенной для термодинамических расчётов и созданной на основе алгоритма, предложенного в [13].
Исходной точкой для моделирования является момент времени, когда выдержка при 1250 °C закончена и образцы охладили до 900 °C. Предполагалось, что фазовый состав в этом случае соответствует равновесному фазовому составу для температуры 1250 °С. В результате термодинамических расчетов было определено, что в равновесии с аустенитом находится карбонитрид, близкий по составу к нитриду титана с составом (Ti0.95,Nb0.05)(C0.013,N0.987)0.98, массовая доля которого составляет 0,00249 %. Средний радиус частиц был принят найденным из эксперимента – 22 нм, а распределение частиц по размерам задавалось как нормальное. Что касается второго карбонитрида – на основе карбида ниобия, – то предполагалось, что после быстрого охлаждения образца до 900 °C он ещё не успел выделиться в заметном количестве, а будет зарождаться и расти при моделировании дальнейшей обработки (деформации и изотермической выдержки). Состав этой фазы был взят согласно термодинамическим расчетам – Nb(C0.68,N0.32)0.97.
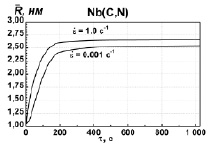
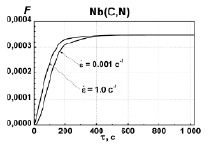
Изменение объемной доли F и среднего радиуса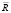 
фазы NbCN при термомеханических обработках со скоростями деформации 1 с–1 и 0,001 с–1 для температуры 900 °C
Результаты расчетов
При моделировании воспроизводились две обработки из работы [12]: первая представляла собой деформацию со скоростью 1 с-1 до достижения степени деформации 1 при температуре 900C суммарной продолжительностью 1025 секунд, а вторая отличалась от нее скоростью деформации, которая была 0,001 с–1. На рисунке приведены расчётные графики изменения среднего радиуса частиц и объемных долей карбонитрида ниобия для двух обработок.
На рисунке видно, что объемная доля растет быстрее, достигая равновесного значения, при скорости деформации в 1 с–1, чем при меньшей скорости деформации. Так же во время деформации с большей скоростью образуются более мелкие частицы. Это можно объяснить тем, что при большей скорости деформации в материале образуется больше дислокаций, которые являются предпочтительными местами зарождения и, как следствие, на них образуется больше частиц. Чем активнее в начальный момент времени идет выделение частиц (которое зависит от дефектности структуры), тем меньше степень пересыщения твердого раствора и тем медленней частицы растут во время последующего отжига.
Графики эволюции карбонитрида на основе TiN не приводятся, поскольку эта фаза термодинамически устойчива и ее объемная доля и размер частиц практически не изменяются во время изотермической выдержки. Кроме того, вклад этой фазы в средний радиус всех частиц, получаемый к концу обработок, незначителен. Таким образом, средний радиус частиц будет определяться, прежде всего, эволюцией карбонитридной фазы NbCN.
Cредний радиус частиц в [12] к концу термомеханической обработки со скоростью деформации 1 с–1 составлял 5 нм, в то время как в наших расчетах он получился 2,65 нм. Для скорости деформации 0,001 с–1 средний радиус частиц составил 3,5 нм в эксперименте и 2,4 нм в расчетах. В целом полученные при помощи моделирования оценки размеров карбонитридных выделений удовлетворительно согласуются с экспериментальными данными.
Заключение
Предложен метод для моделирования эволюции ансамблей карбонитридных выделений комплексного состава при деформации легированной стали в аустенитной области. В основе метода лежит совместное использование моделей, описывающих кинетику, изменение плотности дислокаций при деформации и скорость рекристаллизации, с предложенной нами ранее моделью для описания эволюции карбонитридных выделений. На основе предложенного метода проведено моделирование эволюции ансамблей карбонитридных фаз нескольких составов при деформации и последующей выдержке. Сравнение результатов с экспериментальными данными показало их удовлетворительное согласие.
Работа выполнена в рамках государственного задания по теме «Спин» № АААА-А18-118020290104-2 при поддержке программы фундаментальных исследований УрО РАН (проект № 18–10–2–37).