Популярность модели экономического роста Солоу [1, 2] очень высока с самого момента возникновения. Со временем она стала классической в математической экономике [3–5]. С ней сравнивали более поздние макроэкономические модели [6]. Однако в своих работах Солоу, во-первых основывался на производственной функции Кобба – Дугласа [1, 2], а во-вторых, не написал дифференциального уравнения, описывающего поведение фондовооруженности, для производственной функции более общего характера, которое появилось позже у других авторов [3–5]. Кроме этого, она завоевала популярность и в классической математике [7–9], как в научной, так и учебной литературе. Цель настоящей работы: поставить и решить задачу максимизации интегральной дисконтированной полезности потребления при наличии уравнения связи – дифференциального уравнения, описывающего поведение фондовооруженности, для производственной функции более общего характера, чем производственная функци.яи Кобба – Дугласа.
Постановки оптимизационных задач для уравнения Солоу
Дифференциальное уравнение модели экономического роста Солоу с переменными коэффициентами, которые получены на основании производственной функции произвольного характера [3], имеет вид
, 
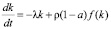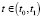. (1)
Здесь t – непрерывное время, измеряющееся в годах, t0 – начальный момент, а t1 – конечный; k = k(t) – фондовооруженность [3, с. 40];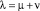 
, где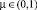 
– доля выбывших за год основных производственных фондов, а 
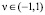– годовой темп прироста числа занятых; 
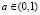– коэффициент прямых затрат (доля промежуточного продукта в валовом общественном продукте); 
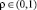– норма накопления (доля валовых инвестиций в валовом внутреннем продукте); x = f(k) – народнохозяйственная производительность труда; а c = c(t) – среднедушевое потребление [3, с. 39–41].
Уравнение для модели Солоу, основанное на производственной функции Кобба – Дугласа является уравнением Бернулли, и поэтому интегрируется в квадратурах [7–9]. Мы в настоящей работе для общности отвлекаемся от производственной функции Кобба – Дугласа и, поскольку уравнение (1) выведено в более общих предположениях, отмечаем, что уравнение (1) в квадратурах не интегрируется [10].
На основании статистических исследований можно сделать вывод, что зависимость народнохозяйственной производительности труда x = f(k) от фондовооруженности k = k(t) описывается производственной функцией Кобба – Дугласа лишь приближенно. Поэтому исследуются модели, в которых присутствует зависимость народнохозяйственной производительности труда от фондовооруженности произвольного характера. Это актуально, так как оптимальная фондовооруженность инвестиционно привлекательна.
Зададим начальное и конечное граничные условия
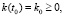(2)
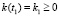(3)
и ставим задачу оптимизации: найти и такое среднедушевое потребление, которое максимизирует интегральную дисконтированную полезность среднедушевого потребления
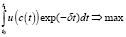, (4)
где u – функция полезности, на свойствах которой мы остановимся в следующем пункте, а δ – коэффициент дисконтирования будущей полезности [3, с. 51, 10, 11]. При этом на среднедушевое потребление можно наложить одно из ограничений
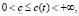(5)
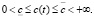(6)
В (4) и (5)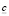 
– среднедушевой прожиточный минимум, а 
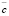– ограничение сверху. Можно наложить еще одно естественное фазовое ограничение на фондовооруженность
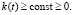(7)
Остановимся, на терминологии. Задачу (1), (2), (3), (4) назовем простой вариационной задачей; задачу (1), (2), (3), (4), (5) – задачей Понтрягина, так же как и задачу (1), (2), (3), (4), (6); задачу (1), (2), (3), (4), (7) назовем вариационной задачей с фазовым ограничением; задачу (1), (2), (3), (4), (5), (7) – задачей Дубовицкого – Милютина [12], так же как и задачу (1). (2), (3), (4), (6), (7).
Во всех сформулированных задачах присутствуют уравнение (1) и граничные условия (2), (3). Это неожиданно, поскольку (1) – обыкновенное дифференциальное уравнение первого порядка и решение его полностью определяется постановкой задачи Коши, то есть начальным или граничным условием, что в данном случае одно и то же, (2). Однако это справедливо, если коэффициенты правой части уравнения (1) известны. В нашем же случае коэффициенты правой части уравнения (1) неизвестны и определяются в ходе рассматриваемой оптимизационной постановки.
Свойства функции полезности
Во всех сформулированных задачах присутствует условие (4). Аналогично [10–12], предполагаем, что полезность среднедушевого потребления характеризует постоянное отвращение к риску по Эрроу – Пратту:
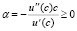. (8)
Экономический смысл (8) становится ясным, если ввести обозначение
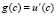, (9)
где g(c) – предельная полезность среднедушевого потребления [11]. С учетом (8) и (9)
,
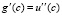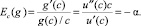(10)
Здесь Ec(g) – эластичность изменения переменной g по переменной c. Мы предполагаем, что g(c) – функция монотонно невозрастающая. Значит, справедливо неравенство α ≥ 0. Противоположное предположение возрастания g(c), очевидно, связано с риском. Поэтому случай, когда g(c) не возрастает, естественно назвать отвращением к риску.
Решением дифференциального уравнения (10) является функция [11]
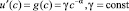, (11)
или
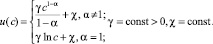(12)
Алгоритм решения простейшей вариационной задачи, основанный на необходимом условии
Для среднедушевого потребления имеется выражение [3, с. 41]
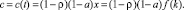(13)
На основании (1) и (13) будем иметь
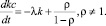(14)
Выражая из (14) среднедушевое потребление, получим
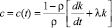, ρ ≠ 0, ρ ≠ 1. (15)
Необходимым условием экстремума в сформулированной нами в настоящей работе простейшей вариационной задаче является справедливость уравнения Эйлера [11]
,
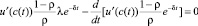ρ ≠ 0, ρ ≠ 1; (16)
которое с учетом (9) может быть записано в виде
,
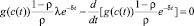ρ ≠ 0, ρ ≠ 1. (17)
Подставляя (15) в (16) или (17), можно заключить, что полученное обыкновенное дифференциальное уравнение относительно неизвестной фондовооруженности k = k(t) будет иметь второй порядок. Поэтому, для однозначного отыскания фондовооруженности нужны оба граничные условия, как начальное (2), так и конечное (3). После того, как будет найдена искомая фондовооруженность k(t), мы из (15) находим и среднедушевое потребление c(t).
Интегрирование уравнения Эйлера
На основании описания алгоритма простейшей вариационной задачи становится ясно, что граничные условия (2) и (3) относятся не к уравнению (1), а к уравнению Эйлера (16) или (17). На первый взгляд, неизвестной функцией в уравнении Эйлера (16) является среднедушевое потребление c = c(t), но в силу выражения этого среднедушевого потребления через фондовооруженность k = k(t) (15), это выражение получено на основании (1), неизвестной функцией в (16) будет уже фондовооруженность. Причем относительно среднедушевого потребления c = c(t) уравнение (16) является уравнением первого порядка, а относительно фондовооруженности k = k(t) – второго.
Введением обозначения
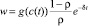, (18)
уравнение Эйлера (17) упрощается
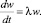(19)
Предполагая в (19) w ≠ 0, разделив на w обе части (19) и интегрируя полученное, имеем
,
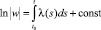или, что то же самое,
, 
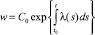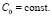(20)
Принимая во внимание (18), из (20) получим
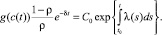
Выражая из последнего равенства предельную полезность среднедушевого потребления, будем иметь
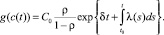(21)
Взяв обратную функцию от предельной полезности среднедушевого потребления, определим из (21) само среднедушевое потребление
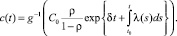(22)
Эквивалентное выражение для среднедушевого потребления может быть получено при помощи разрешения уравнения (11)
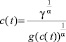, (23)
если в него подставить (21).
Если теперь (22) или (23) при (21) подставить в (15), мы получаем дифференциальное уравнение первого порядка, где неизвестной функцией будет уже фондовооруженность.
Возможные переключения при использовании решений рассматриваемых задач
При рассмотрении любой рассматриваемой в настоящей работе оптимизационной экономической задачи целесообразно использовать следующий подход: как начальное приближение рассмотреть простейшую вариационную задачу, а найдя ее, решение проверить, удовлетворяет ли оно дополнительным условиям (5), (6) и (7). Это всегда можно сделать, так как эти условия являются неравенствами. Если случится, что найденное решение простейшей вариационной задачи этим дополнительным условиям удовлетворяет, то рассматриваемая задача решена.
Однако, полученное решение простейшей вариационной задачи может выйти за рамки какого-нибудь из неравенств (5), (6), (7). Поскольку, предполагается, что условие (2) задано так, что в некоторой малой правой окрестности начального момента времени нужные условия удовлетворяются, то целесообразно несколько сузить рассматриваемый интервал времени, то есть уменьшить t1. Далее, в зависимости от характера поставленной задачи, можно попытаться, уже при новом граничном условии, роль которого будет играть уменьшенное t1, изменить начальные условия так, чтобы решение поставленной задачи на некотором более значительном временном промежутке удовлетворяло нужному из неравенств. Те значения времени, в которых мы изменяем начальные условия, мы и назовем моментами переключения рассматриваемого оптимизационного экономического процесса.
Заключение
В настоящей работе наиболее подробно рассмотрена простейшая вариационная постановка оптимизационной задачи в модели роста Солоу. Однако в результате проведенных исследований получены возможности и более сложных постановок задач оптимального управления, а именно: задачи Понтрягина и задачи Дубовицкого – Милютина.
Роль управления во всех рассмотренных в настоящей работе оптимизационных задачах играет среднедушевое потребление. В достаточно общей постановке проинтегрировано уравнение Эйлера. Можно также рассмотреть оптимизационные задачи в [13–15]. В настоящей работе изучены лишь необходимые условия оптимизации. Достаточные условия на основании (8) полно исследованы в [11].