Проблематика управления производственно-коммерческой деятельностью предприятия и выбора оптимального по рыночному критерию варианта деятельности в производственной сфере в условиях изменчивой внешней среды – с одной стороны, и управления финансовой сферой предприятия с критерием снижения риска финансовой несостоятельности, с другой –важная составляющая научно-практических исследований в области производственного и финансового менеджмента. Казалось бы, что проблематика производственного и финансового планирования взаимосвязана, а принимаемые в этих сферах деятельности предприятия управленческие решения непосредственно влияют друг на друга, что доказано рыночной практикой и отмечено в многочисленных публикациях (например, [1–3]). Однако различия в подходах к решению этих задач в большинстве случаев не позволяют корректно совместить в одной модели задачи оптимизации производственной и финансовой деятельности. Основная причина – противоположный характер используемых критериев и неполная (с позиции двуединой задачи) формализация системы ограничений.
Цель исследования: в этой работе рассмотрим возможный подход к решению комплексной задачи оптимизации производственной и финансовой деятельности предприятия в условиях приоритетного задания критерия оптимальности и системы ограничений.
Будем предполагать, что условия товарных и материальных рынков позволяют планировать производственную программу, обеспечивающую заданный уровень рентабельности осуществляемых затрат (далее в этом контексте используем термин «экономическая эффективность» рабочего капитала PK, понимая под последним постоянные и переменные активы производственной сферы предприятия, учитываемые в калькуляции соответствующих затрат [2]). Для заданного уровня экономической эффективности рабочего капитала вполне оправданной является постановка задачи выбора оптимальной его структуры, понимаемой как соотношение собственных и заемных средств, обеспечивающей максимальный эффект финансового рычага при ограничении на риск структуры капитала. Такая интерпретация традиционной задачи производственного планирования позволяет по-новому взглянуть на дилемму «доходность – риск» производственного сегмента предприятия: предлагается в оценках оптимальной структуры капитала, покрывающего затраты производственной деятельности, учитывать априори его экономическую эффективность.
Рассмотрим необходимую для восприятия нижеследующих математических моделей формализацию показателей предприятия, описывающих критерии и ограничения его деятельности [4].
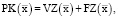(1)
где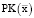 
– рабочий (производственный) капитал операционной сферы предприятия, покрывающий переменные (
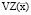) и постоянные (
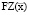) затраты производственной деятельности, определяемые вектором 
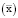производственной программы, причем
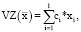(2)
где ci и xi – соответственно удельные переменные затраты и планируемый объем производства продукции i-го наименования.
Если учесть, что валовый маржинальный доход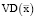 
для вектора рыночных цен 
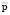составляет величину
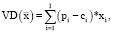(3)
а рабочий капитал формируется за счет собственных (СС) и заемных (ЗС) средств, то экономическая рентабельность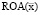 
рабочего капитала для производственной программы, задаваемой вектором 
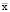, и рассчитанная по операционной прибыли EBIT, определяется выражением
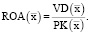(4)
В оценках качества структуры рабочего капитала, так же как и в других работах автора [2, 5], предлагается использовать показатель ROE (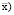
рентабельности собственных средств, рассчитанный по чистой нераспределенной прибыли:
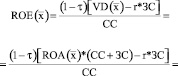
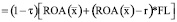, (5)
где τ – ставка налога на прибыль, r – ставка процента по кредиту, FL=ЗС/СС – плечо финансового рычага (соотношение заемных и собственных средств).
В соответствии с основной идеей работы эндогенными (управляемыми) параметрами операционной сферы предприятия являются: планируемый уровень ROA экономической рентабельности затрат (рабочего капитала [6]) и пороговое значение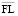 
плеча финансового рычага, определяющее максимальный риск его структуры.
Если структуру рабочего капитала (плечо финансового рычага) обозначить переменной l и принять во внимание нелинейный характер зависимости ставки процента по кредиту r от l, задаваемой функцией r(l), то с учетом фиксированных: ставки налога на прибыль, цен товарного риска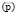 
и рынка материальных факторов производства 
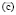, модель выбора оптимальной по критерию максимума рентабельности собственных средств структуры рабочего капитала предприятия задается выражениями
RK(l) = (ROA – r(l))*l > max; (6)
l ≥ 0; (7)
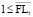(8)
где RK(l) – эффект финансового рычага для структуры рабочего капитала, задаваемый значением l плеча финансового рычага, ROA – отвечающий выбранному варианту производственной деятельности уровень рентабельности активов производственной сферы,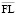 
– пороговое значение плеча финансового рычага.
Экстремальная задача (6)–(8) относится к классу задач нелинейного программирования с выпуклым вверх функционалом (6), что гарантирует единственность решения, удовлетворяющего граничным условиям (7)–(8).
Составим функцию Лагранжа задачи (6)–(8):
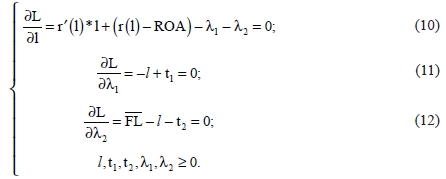
Напомним, что для решения системы уравнений (10)–(12) можно применить теорему Куна – Таккера [7]:
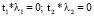. (13)
Так как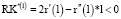 
(учитывая, что 
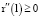), то решение l* системы (10)–(12) является точкой максимума функционала (6), а оптимальная структура l* рабочего капитала обеспечивает рентабельность собственных средств, задаваемую выражением
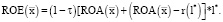(14)
Таким образом, планируя вариант производственной деятельности, задаваемый вектором производственной программы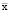 
, в условиях состояния товарных и материальных рынков, описываемых векторами цен 
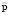и 
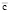соответственно, можно на основе модели (6)–(8) определить оптимальную по критерию рентабельности собственных средств структуру рабочего капитала, задаваемую плечом финансового рычага l* или соответствующим ему коэффициентом автономии:
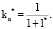(15)
Причем если плечо финансового рычага не превосходит предельного значения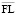 
, то риск структуры капитала не превосходит величины 
.
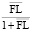Для планируемого варианта производственной программы, задаваемого вектором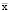 
, и оптимальной структуры рабочего капитала, определяемой на основе значения l* экономическая рентабельность рабочего капитала может быть определена выражением
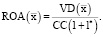(16)
Так как рабочий капитал полностью покрывает затраты производственной деятельности на текущем планово-производственном цикле, то есть
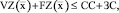(17)
то минимальный объем ССmin собственного финансирования производственной сферы предприятия можно определить выражением
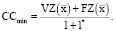(18)
Этот объем обеспечивает планируемое значение экономической рентабельности производственной сферы предприятия с учетом порогового значения риска структуры рабочего капитала.
На основе выражения (6) можно сделать следующий вывод: положительное значение дифференциала финансового рычага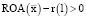 
является необходимым условием целесообразности привлечения в финансирование затрат производственной сферы предприятия заемного капитала.
Таким образом, приемлемый уровень lпр риска структуры рабочего капитала может быть определен на основе неравенства
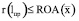(19)
или
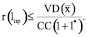(19’)
Рассмотрим математический инструментарий методов конструирования функциональной зависимости в паре «уровень риска структуры капитала – процентная ставка по кредиту». В работе [2] а в качестве такого предложено использовать интерполяционный многочлен Лагранжа [8] степени n – 1, построенный на основе известных значений пары «структура капитала – стоимость заемного финансирования»: сетки узловых точек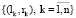 
:
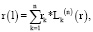(20)
где n – степень интерполяционного многочлена, k – индекс узловой точки;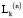 
– лагранжевый коэффициент:
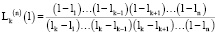. (21)
В цитируемой работе Н.С. Бахвалова, Н.П. Жидкова и Г.М. Кобелькова доказано утверждение о единственности полинома (20) степени n – 1 (на единицу меньше наблюдаемых и используемых в расчетах пар (lk, rk)), принимающего в узлах lk значения rk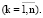 
Для повышения точности аппроксимации функции r = r(l) полиномом (20) в работе [6] рекомендуется использовать следующую процедуру:
1. Расширить множество включаемых в расчеты контрольных точек (узлов) и построить интерполяционные многочлены для различных значений n.
2. Провести контрольные расчеты в новых (не используемых в основном алгоритме) узлах и сравнить r с ее реальным (наблюдаемым) значением.
3. Оценить погрешность и выбрать полином, обеспечивающий наименьшую погрешность.
Проведем демонстрацию модели выбора оптимальной структуры капитала на примере многономенклатурного предприятия ХХ, занятого в строительной отрасли, для которого получим аналитическую зависимость в паре «плечо финансового рычага – стоимость кредита», задаваемую полиномом (17). С учетом выявленной зависимости уточним вариант модели (6)–(8) выбора оптимальной структуры рабочего капитала исследуемого предприятия.
Для построения полинома r(l) будем использовать данные Центрального Банка о средневзвешенных ставках по рублевым кредитам нефинансовым организациям сроком до одного года (табл. 1) и данные пассива баланса предприятия ХХ в разрезе собственных и заемных средств (табл. 2).
За исследуемый временной интервал принимается период с 2012 по 2017 гг., все показатели являются среднегодовыми. По предоставленным данным построим полином (20) четвертой степени:
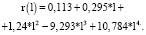(22)
Модель выбора оптимальной по критерию максимума рентабельности собственных средств структуры рабочего капитала предприятия c использованием полинома (22) задается выражениями
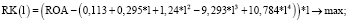(23)
l ≥ 0; (24)
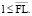(25)
Далее составим функцию Лагранжа для полученной задачи и применим необходимые условия ее экстремума:
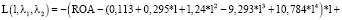
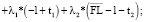(26)
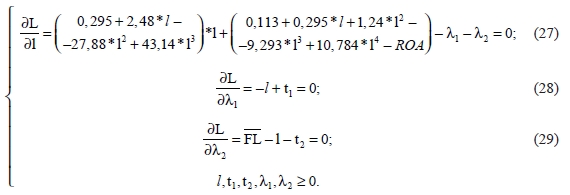
Таблица 1
Средневзвешенная ставка по рублевым кредитам нефинансовым организациям сроком до одного года
|
Год |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
|
r (ставка, %) |
11,37 |
11,49 |
12,32 |
16,46 |
13,70 |
11,17 |
Таблица 2
Заемные и собственные средства строительной компании ХХ
|
Год |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
|
СС (тыс. руб.) |
149 169 |
128 300 |
147 269 |
77 490 |
70 077 |
71 361 |
|
ЗС (тыс. руб.) |
0 |
1 000 |
4 400 |
16 680 |
23 571 |
41 680 |
Таблица 3
Эффект финансового рычага RK(FL) для различных ROA и FL
|
ROA |
FL пороговое |
l* |
RK(l*) |
|
0,5 |
0,2 |
0,2 |
0,06706 |
|
1 |
0,2 |
0,2 |
0,16706 |
|
2 |
0,2 |
0,2 |
0,36706 |
|
5 |
0,2 |
0,2 |
0,96706 |
|
0,5 |
0,5 |
0,5 |
0,20855 |
|
1 |
0,5 |
0,5 |
0,45855 |
|
2 |
0,5 |
0,5 |
0,95855 |
|
5 |
0,5 |
0,5 |
2,45855 |
|
0,5 |
0,8 |
0,57397 |
0,22728 |
|
1 |
0,8 |
0,61879 |
0,52626 |
|
2 |
0,8 |
0,67655 |
1,17609 |
|
5 |
0,8 |
0,77619 |
3,37062 |
Решение системы уравнений (27)–(29) параметрически зависит от значений: планируемой рентабельности ROA рабочего капитала и порогового значения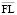 
риска его структуры. Решим построенную задачу нелинейного программирования для различных значений этих параметров (табл. 3).
Для исследуемого предприятия рентабельность ROA рабочего капитала, рассчитанная по формуле (4), принимает значение 0,204 (при валовом доходе, соответствующем точке безубыточности [9, 10]).
Для этого значения рентабельности рабочего капитала решим актуальный вариант модели (23)–(25):
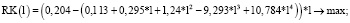(30)
l ≥ 0; (31)
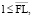(32)
оставляя пороговое значение отношения заемных и собственных средств параметром (табл. 4).
Таблица 4
Решение задачи (30)–(32) для различных уровней риска структуры рабочего капитала
|
FL пороговое |
l* |
RK(l*) |
|
0,2 |
0,2 |
0,01433 |
|
0,5 |
0,5 |
0,03887 |
|
0,8 |
0,8 |
0,12684 |
Рентабельность собственных средств ROE определим, используя найденную экономическую рентабельность рабочего капитала, ставку налога на прибыль 20 % и значение FL, соответствующее 2017 г.
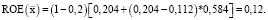(33)
Наибольшую рентабельность собственных средств найдем, используя значение плеча финансового рычага l, соответствующее решению задачи (30)–(32) (табл. 5).
Таблица 5
Максимальные значения рентабельности собственных средств для ROA = 0,204 и различных пороговых значений отношения заемных и собственных средств
|
FL пороговое |
l* |
r(l*) |
ROE* |
|
0,2 |
0,2 |
0,132199 |
0,151613 |
|
0,5 |
0,5 |
0,126103 |
0,131979 |
|
0,8 |
0,8 |
0,045294 |
0,061604 |
Для базового варианта производственной программы компании ХХ по формуле (16) рассчитаем достижимую экономическую рентабельность для оптимальной структуры рабочего капитала при разных пороговых значениях финансового плеча FL. Также определим максимально приемлемые значения отношения заемных и собственных средств, удовлетворяющие нижеследующему неравенству (табл. 6):
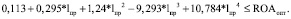(34)
Таблица 6
Достижимые значения экономической рентабельности и отвечающие им максимально приемлемые соотношения (l макс. пр.) заемных и собственных средств для различных пороговых значений FL
|
FL пороговое |
l* |
ROA опт |
l макс. пр |
|
0,2 |
0,2 |
0,85696 |
0,82726 |
|
0,5 |
0,5 |
0,68557 |
0,78113 |
|
0,8 |
0,8 |
0,57130 |
0,77965 |
Переходя к выводам, проведем анализ аналитической зависимости финансового плеча от основных параметров модели: рентабельности ROA рабочего капитала и порогового значения с 
отношения заемных и собственных средств. Для этого по очереди увеличим значения этих показателей на 1 % и определим соответствующие изменения эффекта структуры капитала, используя формулу коэффициента эластичности:
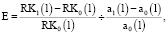(35)
где RK0(l) и RK1(l) – эффекты финансового рычага соответственно до и после изменения задаваемых параметров, a0(l) и a1(l) – параметры модели (ROA и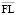 
) соответственно до и после изменения на 1 %.
Таким образом, при изменении рентабельности рабочего капитала на 1 % эффект финансового рычага вырос на 2,95 %, что свидетельствует о его чувствительности к изменению этого показателя. Однако эффект финансового рычага неэластичен по пороговому отношению заемных и собственных средств (при его изменении на 1 % эффект «рычага капитала» изменился менее чем на 1 %).
Заключение
Выводом данного исследования является тот факт, что эффект финансового рычага никак не реагирует на изменения порогового соотношения собственных и заемных средств, однако является эластичным по параметру рентабельности рабочего капитала. Это позволяет утверждать, что для многономенклатурного предприятия в условиях высоко изменчивой рыночной среды проблемы роста экономической эффективности и финансовой устойчивости являются взаимосвязанными.