В конце XX – начале XXI вв. в связи с усложнением финансовой структуры компаний, а также модернизацией экономической конъюнктуры рынков теория и практика инвестиционного анализа столкнулись с проблемой достоверной оценки появившихся инструментов [1]. В новых условиях традиционные и хорошо зарекомендовавшие себя теоретические подходы, математические модели и методы анализа инвестиционных проектов с использованием методологии чистой приведенной стоимости, основанной на анализе дисконтированных денежных потоков, принимаются экономическим сообществом с большой долей осторожности, так как они не позволяют должным образом отобразить возможную гибкость менеджмента компании при пересмотре и адаптации управленческих решений в ответ на неожиданные изменения на рынке. Такая гибкость свойственна финансовым опционам, а в области инвестиционной оценки – стратегическим или реальным опционам [2]. В связи с этим традиционные модели инвестиционного анализа могут быть дополнены, а в некоторых случаях заменены альтернативными подходами, например, методом оценки текущей стоимости опциона колл (пут) с использованием формулы Блэка – Шоулза – Мертона.
Целью исследования является разработка модели реального опциона на управленческое решение относительно момента выполнения инвестиции. В работе используются экономико-математические модели и численные методы оценки эффективности и текущей стоимости инвестиционных проектов с использованием опционного подхода.
В октябре 1997 г. Нобелевский комитет присудил премию по экономике Р. Мертону (Robert Merton) и М. Шоулзу (Myron Scholes) за разработку математической модели, послужившей основой оценки рыночной стоимости производных финансовых инструментов, в частности опционов, и в значительной степени повлиявшей на развитие теории и практики финансовой математики [3].
Общий вид модели Блэка – Шоулза – Мертона расчета стоимости финансового опциона, используемый в работе, следующий [3]:
ce = S0N(d1) – Xe-rTN(d2), (1)
где ce – премия европейского опциона колл, S0 – курс спот акции, Х – цена исполнения опциона, N(d) – функция нормального распределения; величину N(d1) – риск-нейтральная вероятность того, что опцион принесёт выигрыш; N(d2) – вероятность того, что он будет исполнен. Модель Блэка – Шоулза – Мертона однозначно отражает влияние ключевых параметров на стоимость опциона (табл. 1).
Таблица 1
Влияние параметров модели Блэка – Шоулза – Мертона на стоимость опциона колл
|
Фактор |
Влияние на цену опциона |
|
Текущая цена базового актива S0 |
прямое |
|
Цена исполнения опциона Х |
обратное |
|
Время до истечения опциона t |
прямое |
|
Риск (изменчивость цены) актива |
прямое |
|
Безрисковая ставка |
прямое |
|
Промежуточная доходность актива |
обратное |
Помимо непосредственного использования на рынке опционов модель Блэка – Шоулза – Мертона актуальна для оценки страхового возмещения и гарантий, а также для принятия инвестиционных решений [4, 5]. Гарантия по сущностным характеристикам подобна опциону. То же можно сказать о страховом возмещении. Крупнейшие инвестиционные банки используют модель Блэка – Шоулза – Мертона для определения стоимости новых финансовых инструментов. На ее основе крупнейшие корпорации оценивают страховое возмещение, размер которого зависит от будущей стоимости связанных с ним активов. Ford Motors, подписывая договор на поставку деталей с японским производителем, одновременно приобретает опцион пут для защиты от колебаний курса иены относительно доллара, поскольку стоимость опциона растет с падением курса иены.
Модель Блэка – Шоулза – Мертона также широко применятся в области инвестиционной оценки. Теория реальных опционов является продолжением теории финансовых опционов и применяется в оценке нефинансовых (реальных) активов, т.е. в оценке капитальных вложений.
Традиционные методы оценки инвестиционных проектов основаны на анализе дисконтированных денежных потоков (например, концепция NPV) и не позволяют должным образом отобразить гибкость менеджмента компании при пересмотре и адаптации управленческих решений в ответ на неожиданные изменения рынков.
В рамках концепции NPV лежит некий ожидаемый сценарий изменения денежных потоков, что предполагает пассивную стратегию принятия инвестиционных решений. Однако реальный инвестиционный процесс характеризуется неопределенностью и значительно зависит от изменений рыночной конъюнктуры даже в краткосрочной перспективе [6]. По мере поступления новой информации и уменьшения неопределенности рыночного окружения менеджмент должен иметь гибкие инструменты оперативного реагирования и коррекции первоначальной стратегии с целью извлечь выгоду благоприятных будущих возможностей или минимизации текущих потерь. Такая гибкость свойственна финансовым опционам, а в области инвестиционной оценки – стратегическим (реальным) опционам.
Логика теории реальных опционов базируется на тех же принципах, что и теория финансовых опционов: реальный опцион, как и финансовый, имеет значительную гибкость в оценке альтернативных направлений инвестирования. В частности, анализ на основе реальных опционов позволяет определить сроки и объемы конкретных капитальных вложений. Таким образом, процесс принятия решений, основанный на реальных опционах, является систематическим приближением к инвестированию и оценке в условиях высокой неопределенности и конкурентного взаимодействия.
В контексте обсуждения приложений реальных опционов необходимо прояснить различия и сходства между подходом к инвестиционной оценке с помощью реальных опционов и традиционным. Традиционным подходом к оценке инвестиционных проектов является подход, основанный на расчете чистой приведенной стоимости денежных потоков, генерируемых проектом (net present value, NPV). NPV представляет собой разницу между затратами, выполненными в момент времени t0, и возвратными денежными потоками, приведенными к текущему моменту времени. NPV рассчитывается по формуле [7, 8]:
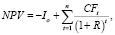 (2)
(2)
где Io – первоначальные инвестиции; CFt – чистый денежный поток в момент времени t; R – ставка дисконтирования; t – период времени; n – срок выполнения проекта.
Менеджеры принимают к реализации проекты, NPV которых больше нуля.
В методе NPV не признается управленческая альтернатива в виде ожидания или задержки начала проекта или поэтапного проекта, в то время как метод реальных опционов предполагает, что решение может быть отложено в условиях непредвиденных обстоятельств, которые могут изменить инвестиционные ожидания. Именно так называемая «управленческая гибкость» обозначается как важная составляющая структурированного анализа проекта, поскольку она является источником дополнительной ценности инвестиционного решения.
Реальные опционы отражают ценность управленческой гибкости на стратегическом горизонте и являются обоснованием интуитивных решений менеджеров, которые не вписываются в рамки традиционной модели NPV. Когда результат инвестирования характеризуется высокой степенью неопределенности, анализ реальных опционов имеет высокую аналитическую ценность: со временем направление изменения стоимости базового актива проясняется, неопределенность снижается, снижается и стоимость опциона, что побуждает менеджеров выбирать момент времени, подходящий для взвешивания и анализа возможных альтернатив реализации инвестиционных проектов.
Различие между опционным и традиционным подходами заключается в том, что последний не учитывает возможность отложить невозвратную инвестицию. Невозвратные инвестиции (sunk costs) представляют собой затраты, которые возникли ранее в прошлом и привели к обязанности произвести выплаты в настоящем или будущем, т.е. настоящие управленческие решения не могут повлиять на уже произведенные выплаты. NPV-анализ предполагает только одну альтернативу: выполнить инвестицию или отказаться от нее (go or no-go decision). Если NPV больше нуля, то результат считается благоприятным и принимается решение об инвестировании. Неблагоприятным последствием применения NPV-анализа является ограниченность реализацией только благоприятных исходов. При этом неопределенность учитывается в премии, что, как показывает инвестиционная практика, не в полной мере соответствует интересам инвесторов (рисунок).
Возможность отложить невозвратную инвестицию подрывает использование модели чистой приведенной стоимости, а значит, и теоретическую основу использования традиционных неоклассических инвестиционных моделей. Что касается предпосылки отсрочки инвестиций, чистая приведенная стоимость не признает альтернативу ожидания или отсрочки начала проекта или поэтапную реализацию проекта.
Что касается предположения об обратимости инвестиций, то концепция NPV подразумевает выбор только одной из двух возможных альтернатив: либо инвестиции обратимы, т.е. имеется возможность отмены решения в любой момент времени, либо, если инвестиции необратимы, решение об инвестировании принимается сейчас без возможности изменить его в будущем.
Ввиду перечисленных выше различий в подходах к оценке невозвратных инвестиций оценка проекта на основе реального опциона всегда больше или равна оценке с использованием чистой приведенной стоимости. В редких случаях оценка на основе NPV совпадает с опционной оценкой: по прошествии времени, когда реальный опцион «истёк». Когда событие, относительно которого был оценен реальный опцион, наступило, неопределенность, связанная с этим событием, становится нулевой, тем самым чистая приведенная стоимость становится равна текущей стоимости активов проекта за вычетом осуществленных по проекту затрат. В терминологии опционов:
NPV = S – E, (3)
где S – текущая стоимость базового актива; E – цена исполнения опциона.
Указанное выше условие равенства оценок позволяет определить возникновение ситуации, когда оценки реального опциона и NPV расходятся: неопределенности будущих изменений цен, процентных ставок, потребительских предпочтений и технологий. Реальные опционы позволяют менеджерам учитывать эти эффекты.
Реальный опцион может быть рассчитан для инвестиций в капитальные активы. Поскольку реальный опцион имеет черты европейского опциона-колл, могут использоваться те же инструменты оценки, что и для опционов на финансовых рынках. Невозвратные инвестиции аналогичны европейскому опциону-колл: владелец опциона имеет право, но не обязательство заплатить цену исполнения опциона за инвестицию.
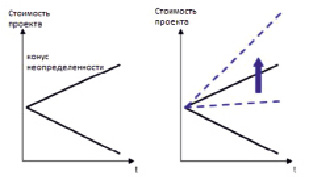
а) б)
Конус неопределенности в традиционном (а) и опционном (б) подходах к оценке инвестиций
Таблица 2
Соответствие параметров модели Блэка – Шоулза – Мертона и модели реального опциона*
|
Параметр |
Модель Блэка – Шоулза |
Модель реального опциона |
|
S0 |
цена базового актива |
текущая стоимость объекта инвестирования |
|
X |
цена исполнения опциона |
вложения, которые необходимо выполнить, чтобы достичь цели проекта |
|
T |
время до истечения опциона |
период времени, на который отложено решение об инвестировании |
|
R |
безрисковая ставка процента, соответствующая сроку опциона |
безрисковая ставка процента, соответствующая сроку опциона |
|
σ |
дисперсия доходности актива |
степень неопределенности или риска проекта |
Примечание. *Общий вид модели Блэка – Шоулза – Мертона соответствует приведенному выше (1).
К настоящему времени метод реальных опционов для оценки инвестиционных проектов применяется в основном в таких отраслях, как добыча полезных ископаемых, энергетика, фармацевтика, которые характеризуются высокой степенью неопределенности относительно исходов инвестирования в бизнес-процессы, а также для оценки и принятия стратегических решений в строительной отрасли.
Применение метода реальных опционов не ограничивается оценкой экономического эффекта от инвестирования. Метод может быть использован и для расчета оптимального момента выполнения инвестиции. Постановка задачи в этом случае такая: на какое количество периодов следует отложить инвестицию для достижения максимального экономического эффекта отсрочки?
В рамках этой задачи реальный опцион является опционом на отсрочку в том смысле, что лицо, принимающее решения, может отложить его, чтобы определить, оправдывает ли экзогенная неопределенность (например, рыночные цены затрат на строительство нового предприятия) ожидания инвестора. Из приведенного следует, что модель реального опциона на управленческое решение относительно момента выполнения инвестиции применима для проектов с поэтапным инвестированием.
Для построения модели реального опциона необходимо установить, как в контексте решаемой задачи будут преобразованы параметры «традиционной» модели Блэка – Шоулза – Мертона (табл. 2).
В контексте реального опциона параметры модели могут быть интерпретированы следующим образом: S0N(d1) – ожидаемое значение базового актива, если на момент истечения срока действия опциона текущее значение больше, чем инвестиционная стоимость; N(d2) – риск-нейтральная вероятность события, что текущая стоимость базового актива будет выше, чем стоимость инвестиции на момент истечения срока опциона; e-rT – текущая стоимость инвестиции по истечении срока опциона.
В рамках текущей задачи открытым остается вопрос о подходах к оценке параметров S0, X, ϭ. Принимая во внимание теоретическое обоснование выбора значений параметра S0, X, для их расчета можем использовать элементы традиционной модели, определив S0 как номинальную стоимость затрат на проект, а X – приведенную стоимость денежных потоков проекта. Такой подход к оценке параметров модели реального опциона соответствует их значениям в аналогичной модели финансового опциона (1).
Наиболее «непрозрачным» является параметр ϭ, представляющий собой по определению степень неопределенности (риска) проекта. В качестве возможных подходов к оценке ϭ можно использовать следующие: имитационное моделирование по методу Монте-Карло, метод сценариев, методы теории игр.
Представленная модель реального опциона на управленческое решение относительно момента выполнения инвестиции отражает возможность ответа на вопрос: «Оправдано ли решение отложить инвестицию на заданное количество периодов T?» Однако эта же модель может быть модифицирована путем представления в виде оптимизационной относительно параметра времени t с ограничением на уровень риска:
ce = S0N(d1) – Xe-rtN(d2)>max,
ϭ < ϭс , (4)
t∈Z.
Решение модели (4) дает ответ на вопрос: «На какое количество периодов необходимо отложить инвестирование для получения максимального эффекта отсрочки, выраженного стоимостью реального опциона на управленческое решение относительно момента выполнения инвестиции?» Данная оптимизационная модель требует дальнейшего уточнения в части ограничений на параметры S0, X.
Заключение
В заключение отметим, что в академических кругах формируется мнение о том, что опционный подход является единственным верным к принятию инвестиционных решений, а метод чистой приведенной стоимости представляет лишь частный случай в рамках общей теории выбора. Реальные опционы являются отражением гибкости руководства и способности реагировать на изменения со временем. В качестве ценных нематериальных активов они выступают не только для фирм и деловых агентов [9].
Разумеется, опционный подход не может полностью заменить NPV-анализ. Оценка реального опциона не является вариантом полного инвестиционного анализа: она должна использоваться как дополнительная уточняющая оценка наряду с существующими традиционными моделями оценки капитальных затрат. Анализ реальных опционов позволяет увеличить общее понимание менеджером инвестиционного решения и помогает лицам, принимающим решения, учитывать области неопределенности, которые не учитываются в показателе NPV.
Приведенную в работе модель опциона на управленческое решение требуется апробировать на реальных проектах, после чего можно будет сделать вывод о ее практической значимости.



