Для неинституционального инвестора важной является задача формирования оптимального портфеля ценных бумаг, отражающего его предпочтения относительно доходности и риска. Неинституциональный инвестор – непрофессиональный участник российского фондового рынка, осуществляющий операцию покупки/продажи финансовых активов с участием профессионального участника – брокера или управляющей компании. Поддержкой принятия инвестиционных решений непрофессиональных инвесторов являются экономико-математические модели. Однако большинство моделей в качестве исходной предпосылки используют утверждение, что продаваемые финансовые активы бесконечно делимы, что не соответствует реалиям фондового рынка, где ценные бумаги продаются целочисленными лотами. Поэтому учет фактора дискретности в моделях управления финансовым портфелем является актуальной проблемой портфельного инвестирования.
Классическая задача управления портфелем представлена в работе Г. Марковица [1], который предложил метод выбора оптимальной структуры портфеля ценных бумаг в условиях риска. Идея заключается в том, что инвестор принимает решение на основе математического ожидания доходности – оценка доходности финансового портфеля, и дисперсии (или среднего квадратического отклонения доходности) – оценка риска. Обладая информацией о прошлых значениях доходностей ценных бумаг, непрофессиональный инвестор с использованием математической модели формирует индивидуальный портфель с учетом риска и планируемой доходности.
В качестве искомых величин в модели Г. Марковиц использовал «веса» ценных бумаг (доли активов в совокупном портфеле), которые определяются выражением
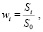 (1)
(1)
где Si – средства, на которые приобретаются акции i-го эмитента, S0 – начальный бюджет инвестора.
Модель Г. Марковица имеет следующий вид:
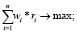 (2)
(2)
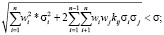 (3)
(3)
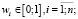 (4)
(4)
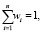 (5)
(5)
где ri – средняя доходность i-го актива; wi – доля i-го актива в портфеле; σi – среднее квадратическое отклонение доходности i-го актива; а kij – коэффициент корреляции доходности i-го и j-го активов; σ – приемлемое для инвестора значение риска.
Коэффициент корреляции вычисляется по формуле
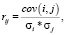 (6)
(6)
где cov(i, j) – ковариация доходностей i-го и j-го активов, σi, σj – волатильность i-й и j-й бумаги.
Г. Марковец предложил метод снижения риска, при котором инвесторы одновременно оперируют активами с разными трендами доходности и риска [2]. Наличие в портфеле активов с отрицательным коэффициентом корреляции снижает общий риск портфеля и указывает на необходимость его диверсификации в сравнении с выбором наиболее доходной акции.
Модель (2)–(5) – задача максимизации доходности портфеля с ограничением на риск.
Однако задачу определения структуры оптимального портфеля можно представить и как задачу на минимум риска при ограничении на доходность портфеля. Именно в такой постановке Г. Марковиц впервые представил эту задачу в работе 1952 г.
Модель Г. Марковица использует следующие допущения [3]:
– инвестирование осуществляется за один холдинговый период. В начальный момент (t = 0) инвестор вкладывает сумму денег S0 в портфель акций. В конце холдингового периода (t = 1) инвестор продает акции и полученный доход капитализирует по своему усмотрению;
– рынки ценных бумаг являются эффективными: инвесторы имеют доступ к информации о ценах и торгах и не могут оказывать единоличного влияния на рынок, сделки с ценными бумагами осуществляются без трансакционных (в данном случае дополнительных) затрат;
– доходность i-й акции за будущий холдинговый период равна средней арифметической величине ее доходностей на предыдущих шагах;
– запрет на продажу без покрытия. Согласно [4], продажа без покрытия – случай, при котором инвестор приобретает акцию в кредит и одновременно принимает обязательство вернуть ее в момент времени t = 1. Он продает приобретенную акцию в момент t = 0. Для того, чтобы вернуть бумаги по истечению указанного в обязательствах периода, он должен купить их по курсу, который будет преобладать по окончанию этого периода. Данное допущение выражается в виде ограничения на неотрицательность долей wi ценных бумаг.
Решение задачи оптимизации структуры портфеля неинституционального инвестора предполагает нахождение долей 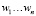 из имеющихся у инвестора в момент t = 0 инвестированных средств
из имеющихся у инвестора в момент t = 0 инвестированных средств 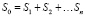 , которые он направит на приобретение акций портфеля.
, которые он направит на приобретение акций портфеля.
После покупки акций в момент t = 0 инвестор ожидаемо имеет остатки начального бюджета, и так как предполагается, что активы, включаемые в портфель, бесконечно делимы (что противоречит фактору дискретности торгуемых лотов), то остаток инвестиционных средств переходит на следующий инвестиционный шаг. Таким образом, фактор дискретности является важным аспектом выбора оптимального портфеля неинституционального инвестора.
Ранее возможные подходы к его учету в модели Г. Марковица были предложены А.В. Мищенко, А.С. Сазоновой [5], Л.С. Мангущевой [6], М.А. Халиковым, А.М. Антиколь [7, 8].
В целочисленной модели Г. Марковица в качестве искомой величины выступают xi – количество лотов акций i-го эмитента в портфеле. Инвестиционные вложения в i-ю акцию Si в формуле (1) определяются выражением
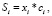 (7)
(7)
где xi – количество приобретаемых акций i-го эмитента, ci – текущая цена i-й акции.
Так как активы можно приобретать только лотами, то доли активов ценных бумаг, вложенных в портфель, в традиционной постановке модели Г. Марковица с учетом (1) и (7) определяются следующим образом:
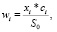 (8)
(8)
где xi – количество лотов акций i-го эмитента в портфеле, ci – цена i-го актива, S0 – начальный бюджет инвестора.
Подставим выражение (8) в ограничение на риск (3) и критерий (2) модели (2)–(5). Получим новую модель, в которой xi – количество приобретаемых лотов акций i-го эмитента в портфеле ценных бумаг – искомая переменная; ci – текущие цены активов, S0 – начальный бюджет инвестора. Эти параметры считаются известными на начальный момент времени, так же как и приемлемый для инвестора уровень риска σ.
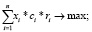 (9)
(9)
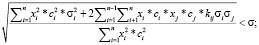 (10)
(10)
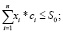 (11)
(11)
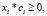 (12)
(12)
где ri – средняя доходность актива i; xi – количество лотов акций i-го эмитента в портфеле; ci – текущая цена i-й акции; S0 – начальный бюджет; σi – среднее квадратическое отклонение доходностей активов; а kij – коэффициент корреляции доходности i-го и j-го активов.
Произведем замену переменной 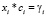 (величина начального бюджета S0, которую инвестор планирует разместить на приобретение лотов акций i-го эмитента).
(величина начального бюджета S0, которую инвестор планирует разместить на приобретение лотов акций i-го эмитента).
Запишем полученную оптимизационную модель:
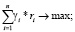 (13)
(13)
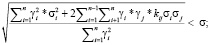 (14)
(14)
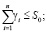 (15)
(15)
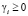 . (16)
. (16)
Постановка задачи с учетом новой переменной γi позволяет непрофессиональному инвестору сократить объем расчетов и вместо долей wi акций каждого эмитента находить суммы γi, которые следует потратить на покупку ценных бумаг. Однако данная постановка не учитывает фактор дискретности приобретаемых лотов.
Добавим ограничение на целочисленность xi – количество приобретаемых лотов акций i-го эмитента и получим новую постановку задачи с учетом дискретности приобретаемых лотов:
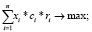 (17)
(17)
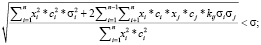 (18)
(18)
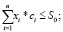 (19)
(19)
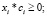 (20)
(20)
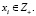 (21)
(21)
Эта задача представляет собой задачу целочисленного нелинейного программирования, которая может быть решена с помощью идеи метода ветвей и границ [9], адаптированного к условиям рассматриваемой модели. Класс нелинейных целочисленных задач относится к классу NP-полных по Тьюрингу проблем и, как следствие, не может быть решен с использованием известных методов оптимизации.
Однако в нашем случае ограничение на риск (19) является выпуклым, а критерий задачи (18) линейным. Поэтому можно использовать основную идею метода ветвей и границ, связанную с представлением области допустимых значений оптимизационной задачи в виде прямой суммы непересекающихся выпуклых областей, для каждой из которых оптимальное решение целочисленной задачи может быть получено с использованием известных методов оптимизации (например, сведением к линейной задаче).
Приведем сравнительный анализ портфелей, полученных на основе традиционной постановки задачи Г. Марковица (2)–(5) и его целочисленной «версии» (17)–(21).
Сделаем предположение, что на структуру портфеля в целочисленной постановке оказывают влияние факторы:
– ликвидности портфеля (низко-, высоколиквидный или диверсифицированный);
– величины начального бюджета инвестора;
– приемлемого для инвестора уровня риска.
Сформируем три портфеля ценных бумаг российских эмитентов – высоко-, низколиквидные и диверсифицированный.
Первый портфель включает обыкновенные акции высокого и среднего уровня ликвидности следующих эмитентов: Норильский никель (GMKN), Магнит (MGNT), Новолипецкий МК (NLMK), Лукойл (LKOH), ММК (MAGN) и Аэрофлот (AFLT), Газпром (GAZP), Мечел (MTLR), Московская биржа (MOEX), Россети (RSTI), Русгидро (HYDR), Роснефть (ROSN) [10, 11] (краткая информация о выбранных эмитентах представлена в табл. 1).
Второй портфель включает обыкновенные акции низкого уровня ликвидности и состоит из двенадцати акций следующих российских эмитентов: Акрон (AKRN), Аптека 36 и 6 (APTK), Белон (BLNG), Дикси (DIXY), Камаз (KMAZ), МГТС (MTSS), Мвидео (MVID), Русолово (ROLO), Квадра (TGKD), Банк Уралсиб (USBN), ЗИЛ (ZILL), Звезда (ZVEZ) [10, 11] – (табл. 2).
Третий портфель (диверсифицированный) включает двадцать две акции российских эмитентов разного уровня ликвидности: Норильский Никель (GMKN), Новолипецкий МК (NLMK), Лукойл (LKOH), ММК (MAGN), Газпром (GAZP), Мечел (MTLR), Московская биржа (MOEX), Россети (RSTI), Русгидро (HYDR), Роснефть (ROSN), Акрон (AKRN), Аптека 36 и 6, Белон (BLNG), Дикси (DIXY), Камаз (KMAZ), МГТС (MTSS), Мвидео (MVID), Русолово (ROLO), Квадра (TGKD), Банк Уралсиб (USBN), ЗИЛ (ZILL), Звезда (ZVEZ) [10, 11] – (табл. 3).
Таблица 1
Доходности и волатильность акций, входящих в высоколиквидный портфель
|
Акции |
Ср. доходность, % |
СКО доходностей |
Текущая цена |
|
Газпром |
0,081 |
0,00857 |
122,34 |
|
Лукойл |
0,165 |
0,01285 |
2991,5 |
|
Магнит |
0,145 |
0,01323 |
10340 |
|
Мечел |
0,348 |
0,02164 |
152,5 |
|
ММК |
0,562 |
0,01929 |
42,7 |
|
Моск. биржа |
0,185 |
0,01470 |
116,3 |
|
НЛМК |
0,323 |
0,01584 |
127,5 |
|
Нор. никель |
0,263 |
0,01394 |
9710 |
|
Роснефть |
0,053 |
0,01090 |
316,7 |
|
Россети |
0,524 |
0,02033 |
1,0579 |
|
Русгидро |
0,052 |
0,01451 |
0,813 |
|
Аэрофлот |
0,118 |
0,01942 |
187 |
Примечание. Средние показатели доходности и волатильности рассчитаны авторами на основе исходных данных о ценах закрытия акций за период июнь – октябрь 2017 г. Уровень ликвидности ценных бумаг определен по классификации Московской биржи.
Таблица 2
Доходности и волатильность акций, входящих в низколиквидный портфель
|
Акции |
Ср. доходность, % |
СКО доходностей |
Текущая цена |
|
Акрон |
0,229 |
0,01227 |
4109 |
|
Аптека 36 и 6 |
0,048 |
0,01694 |
8,51 |
|
Белон |
0,059 |
0,02373 |
2,79 |
|
Дикси |
0,316 |
0,01769 |
321,8 |
|
Камаз |
0,035 |
0,01353 |
52,55 |
|
МГТС |
0,088 |
0,02685 |
1525 |
|
МВидео |
0,033 |
0,01605 |
408,7 |
|
Русолово |
0,329 |
0,02036 |
3,08 |
|
Квадра |
0,217 |
0,01804 |
0,003695 |
|
Банк Уралсиб |
0,008 |
0,01712 |
0,0867 |
|
ЗИЛ |
0,019 |
0,02680 |
1090 |
|
Звезда |
0,084 |
0,05382 |
4,22 |
Примечание. Средние показатели доходности и волатильности рассчитаны авторами на основе исходных данных о ценах закрытия акций за период июнь – октябрь 2017 г. Уровень ликвидности ценных бумаг определен по классификации Московской биржи.
Таблица 3
Доходности и волатильность акций, входящих в диверсифицированный портфель
|
Акции |
Уровень ликвидности |
Ср. доходность, % |
СКО доходностей |
Текущая цена |
|
Газпром |
высокий |
0,1336 |
0,00971 |
142,99 |
|
Нор. Никель |
высокий |
0,2422 |
0,01568 |
11750 |
|
Русгидро |
средний |
0,0173 |
0,01523 |
0,7699 |
|
Лукойл |
высокий |
0,2439 |
0,01227 |
3876,5 |
|
ММК |
средний |
0,2967 |
0,01682 |
45,74 |
|
Моск. биржа |
высокий |
0,0630 |
0,01532 |
113,84 |
|
Мечел |
высокий |
0,1241 |
0,02166 |
154,95 |
|
НЛМК |
высокий |
0,2555 |
0,01613 |
152,5 |
|
Роснефть |
высокий |
0,0034 |
0,01212 |
319,95 |
|
Россети |
средний |
0,0398 |
0,01960 |
0,825 |
|
Акрон |
низкий |
0,2196 |
0,01219 |
4109 |
|
Аптека 36 и 6 |
низкий |
0,0326 |
0,01698 |
8,51 |
|
Белон |
низкий |
0,0762 |
0,02392 |
2,79 |
|
Дикси |
низкий |
0,3289 |
0,01773 |
321,8 |
|
Камаз |
низкий |
0,0297 |
0,01367 |
52,55 |
|
МГТС |
низкий |
0,0811 |
0,02699 |
1525 |
|
МВидео |
низкий |
0,0327 |
0,01621 |
408,7 |
|
Русолово |
низкий |
0,3210 |
0,02055 |
3,08 |
|
Квадра |
низкий |
0,2308 |
0,01819 |
0,003695 |
|
Банк Уралсиб |
низкий |
0,0187 |
0,01724 |
0,0867 |
|
ЗИЛ |
низкий |
0,0000 |
0,02693 |
1090 |
|
Звезда |
низкий |
0,0424 |
0,05427 |
4,22 |
Примечание. Средние показатели доходности и волатильности рассчитаны авторами на основе исходных данных о ценах закрытия акций за период август – январь 2017/2018 гг.
Таблица 4
Сравнение структур портфелей по «классической» и «целочисленной» постановкам модели Г. Марковица
|
Высоколиквидный портфель |
Низколиквидный портфель |
Диверсифицированный портфель |
||||
|
Риск/Бюджет |
100 тыс. руб. |
1 млн руб. |
100 тыс. руб. |
1 млн руб. |
100 тыс. руб. |
1 млн руб. |
|
0,006 |
+ |
+ |
– |
+ |
– |
+ |
|
0,007 |
+ |
+ |
– |
+ |
– |
+ |
|
0,008 |
+ |
+ |
– |
+ |
– |
+ |
|
0,009 |
+ |
+ |
– |
+ |
– |
– |
|
0,01 |
– |
+ |
– |
+ |
– |
– |
|
0,011 |
– |
+ |
– |
+ |
– |
+ |
|
0,012 |
– |
+ |
– |
– |
– |
+ |
|
0,013 |
+ |
+ |
– |
– |
– |
+ |
|
0,02 |
– |
+ |
– |
– |
– |
– |
Пусть начальный бюджет неинституционального инвестора составляет либо S0 = 100 тыс. руб., либо S0 = 1 млн руб. Приемлемый уровень риска от 0,006 до 0,02.
Приведем расчеты оптимальных портфелей для разных бюджетов и разных уровней риска. Для решения задач (2)–(5) и (17)–(21) используем табличный процессор Excel «Поиск решения» [12].
Представим результаты в табл. 4. Знак «+» означает, что структуры портфелей, полученные по двум моделям, совпадают. Знак «–» означает, что эти структуры различны (считаем, что структуры портфелей, построенные по двум моделям, различны, если присутствует хотя бы одна акция, которая входит в оптимальный портфель, полученный по одной модели, но не входит в другой).
Полученные результаты свидетельствуют о том, что все выделенные выше факторы (уровень ликвидности, начальный бюджет, приемлемый уровень риска) оказали влияние на структуру портфеля в условиях целочисленности приобретаемых лотов.
Начальный бюджет инвестора повлиял на структуру портфелей всех уровней ликвидности, особенно на низколиквидный и диверсифицированный портфели. Состав высоколиквидного портфеля менее подвержен фактору изменения начального бюджета при низком уровне риска («осторожный» инвестор). Результаты табл. 4 показывают, что при увеличении бюджета структура портфеля с учетом фактора дискретности приближается к структуре портфеля, полученной по классической постановке модели Г. Марковица. В случае высоколиквидных ценных бумаг увеличение бюджета способствовало преодолению различий между структурами, полученными по двум моделям для всех рассматриваемых уровней риска.
Отметим, что при низком риске (0,006–0,009) структуры высоколиквидного портфеля совпадают. При низком и среднем риске (0,006–0,013) в случае большого объема инвестиционных средств структуры низколиквидного и диверсифицированного портфелей частично совпадают. При высоком риске (0,02) структуры портфелей различны для всех уровней ликвидности портфелей за исключением высоколиквидного портфеля с большим объемом начальных инвестиций.
Заключение
Таким образом, согласно проведенному анализу, можно сделать вывод, что учет дискретности в модели Г. Марковица оказывает влияние на оптимальную структуру портфеля ценных бумаг по сравнению со структурой, полученной по классической постановке этой задачи. При условии целочисленности различие в структуре финансового портфеля наблюдается в разрезе факторов начального бюджета, приемлемого риска и уровня ликвидности. Полученные выводы подтверждают, что фактор дискретности лотов ценных бумаг является важным аспектом портфельного инвестирования.



