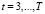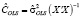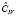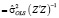Целью исследования является анализ и моделирование золотовалютных резервов с привлечением аппарата моделей для панельных данных. Статистическая выборка панельных данных, представляющих динамику запасов золота восьми стран: Германии, Франции, США, Китая, России, Нидерландов, Швейцарии и Японии – за семнадцать лет с 2000 по 2016 г. была сформирована из открытых баз данных Всемирного банка [1] и Всемирного золотого совета [2]. В качестве регрессоров модели использован ВНП каждой страны и запас золота (лаговые переменные). При формировании панельных данных была решена задача замены пропущенных значений, которые требовали либо удаления, что существенно сужает исследовательские возможности, либо их замещения. Замена пропущенных наблюдений выполнена с помощью пакета Multivariate Imputation by Chained Equations, предоставляемым языком программирования R.
Страны, которые мы рассматриваем в нашем исследовании, можно разделить на две группы. В первую группу входят технически развитые страны. В этих странах золото широко используется в различных областях техники и промышленных отраслях, а также для изготовления ювелирных изделий. К этим странам относятся Япония, США и Германия. В этих странах золото выступает как индикатор развития высоких технологий. За рассматриваемый период в этих странах не наблюдается тенденций к росту запасов золота. Вторая группа – это страны, интенсивно наращивающие запасы золота. Это Россия и Китай (рис. 1–2). Россия активно скупает золото. Причиной этого могут быть санкции США и Евросоюза, которые вынуждают российское руководство относиться к резервам в долларах и евро с большой осторожностью. Китай также стремится увеличивать свои золотые резервы.
Многие аналитики считают, что Китай и Россия, скорее всего, будут увеличивать запасы золота для защиты от экономической неопределённости в будущем.
В настоящее время наблюдается ситуация, когда финансовые власти России продают долговые обязательства правительства США ускоренными темпами. При этом Центробанк России продолжает скупать золото у российских золотодобытчиков максимальными за последние 12 лет объёмами. Сейчас Россия находится на пятом месте среди стран – держателей золота, обогнав недавно Китай. Впереди находятся США, Германия, Италия и Франция [3].
Выбор эконометрического инструментария
Выборочные данные состоят из наблюдений однотипных объектов (8 стран) в течение небольшого периода времени (17 лет). Поэтому в качестве инструмента выбран аппарат моделей для панельных данных, позволяющий выполнять оценивание при небольшом объеме выборки для отдельных экономических единиц [4–6]. Одним из преимуществ аппарата панельных данных является способность учитывать индивидуальную динамику (динамику на «индивидуальном уровне» [7, 8]), что особенно важно при моделировании зависимости объёма золотых резервов от ВВП страны, в которой текущий объем существенно зависит от объема и ВВП предыдущего года. Основными регрессионными моделями, применяемыми к панельным данным, являются:
- объединённая модель (Pooled model, Pool): спецификация не учитывает индивидуальные особенности объектов
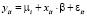 ,
, 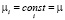 , (1)
, (1)
где yit – зависимая переменная, xit – вектор-строка регрессоров (размерностью k), εit – случайное возмущение; i = 1,..., n, t = 1,..., T, n – число объектов (панелей), T – число наблюдений в рамках одной панели, μ = const – постоянное для всех объектов значение свободного члена – параметр «местоположения», 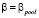 – вектор параметров «влияния», постоянный для всех объектов (панелей);
– вектор параметров «влияния», постоянный для всех объектов (панелей);
- модель с фиксированными эффектами (fixed effect model, FE): гетерогенность объектов учитывается индивидуальными параметрами местоположения μi,
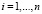
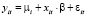 ,
, 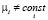 , (2)
, (2)
- модель со случайными эффектами (random effect model, RE): гетерогенность объектов учитывается независящей от времени специфической составляющей ошибки mi:
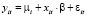 ,
, 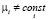 ,
, 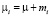 ,
,
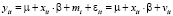 . (3)
. (3)
В статических моделях (1)–(3) предполагается, что 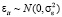 , и оценки параметров получаются состоятельными и эффективными, при обоснованном выборе характера эффектов.
, и оценки параметров получаются состоятельными и эффективными, при обоснованном выборе характера эффектов.
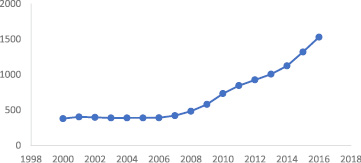
Рис. 1. Динамика запасов золота в России
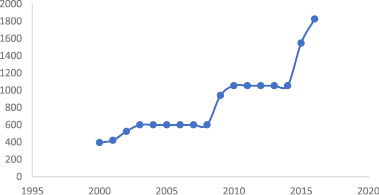
Рис. 2. Динамика запасов золота в Китае
Результаты оценивания
Формальное применение аппарата моделей для панельных данных приводит к следующему результату:
Объединенная модель:
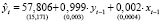 ,
,
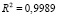 , (4)
, (4)
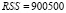 ,
, 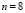 – число панелей, T = 16 – число наблюдений в рамках одной панели, nT = 128 – объём панельных данных. В скобках под оценками параметров приводятся их стандартные ошибки, RSS (Residuals Sum of Squares) – сумма квадратов остатков.
– число панелей, T = 16 – число наблюдений в рамках одной панели, nT = 128 – объём панельных данных. В скобках под оценками параметров приводятся их стандартные ошибки, RSS (Residuals Sum of Squares) – сумма квадратов остатков.
Модель с фиксированными эффектами:
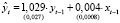 ,
, 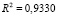 ,
,
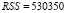 . (5)
. (5)
В оцененной модели (5) приводятся оценки параметров влияния (общие для всех панелей). Для получения их состоятельных оценок, в модели с фиксированными эффектами, используется процедура раздельного оценивания параметров влияния и местоположения. Для спецификации в матричном виде [9, 10]
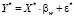 , (6)
, (6)
где 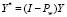 – вектор значений эндогенных переменных, центрированных по индивидуальным средним (средним по каждой панели),
– вектор значений эндогенных переменных, центрированных по индивидуальным средним (средним по каждой панели), 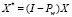 – матрица регрессоров, центрированных по индивидуальным средним,
– матрица регрессоров, центрированных по индивидуальным средним, 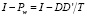 – оператор внутригруппового преобразования (центрирования по индивидуальным средним),
– оператор внутригруппового преобразования (центрирования по индивидуальным средним),
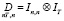 – матрица фиктивных переменных, учитывающая гетерогенность панельных данных в моделях с фиксированным эффектом,
– матрица фиктивных переменных, учитывающая гетерогенность панельных данных в моделях с фиксированным эффектом,
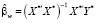 , (7)
, (7)
– вектор МНК-оценок параметров влияния. Оценки параметров местоположения вычисляются по оценкам параметров влияния:
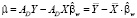 , (8)
, (8)
где
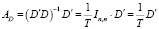
– оператор формирования вектора индивидуальных средних. В табл. 1 приводятся оценки параметров местоположения, полученные в рамках раздельной процедуры оценивания (5)–(8).
Модель со случайными эффектами:
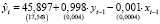 ,
,
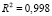 ,
, 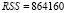 . (9)
. (9)
Минимальную сумму квадратов остатков обеспечивает модель с фиксированными эффектами. Адекватность этой модели подтверждается и тестированием характера гетерогенных эффектов. F-тест (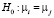 , функция в программной среде R pFtest()) [11]:
, функция в программной среде R pFtest()) [11]:
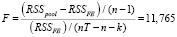 ,
,
p-value = 2,708e-11,
где k – число параметров влияния, RSSpool – сумма квадратов остатков объединённой модели, RSSFE – сумма квадратов остатков модели с фиксированными эффектами. Тест множителей Лагранжа (тестирование Pooled-модели против модели RE, 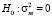 , (функция в программной среде R plmtest()):
, (функция в программной среде R plmtest()):
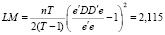 ,
,
p-value = 0,146,
где e – вектор-столбец остатков в объединённой модели, D – матрица фиктивных переменных, не выявил значимых случайных эффектов для различных стран. Тест Хаусмана (тестирование модели RE против модели FE,  , (функция в программной среде R phtest()):
, (функция в программной среде R phtest()):
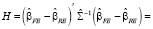
= 84,733 > 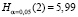 ,
,
где 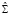 – оценка автоковариационной матрицы вектора
– оценка автоковариационной матрицы вектора 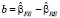 , отклоняет нулевую гипотезу об адекватности модели со случайными эффектами.
, отклоняет нулевую гипотезу об адекватности модели со случайными эффектами.
Тестирование наличия автокорреляции в моделях для панельных данных может быть выполнено при помощи обобщенной статистики Дарбина – Уотсона в рамках модели с фиксированными эффектами, так как оценки параметров модели с FE состоятельны и в случае адекватности модели со случайными эффектами [7, 12]:
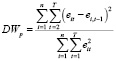 = 1,203,
= 1,203,
p-value = 2.212e-06. (10)
Так как области неопределенности обобщенного теста являются малыми и изменения критических значений, в зависимости от параметров (n, T, K) незначительные, то полученный результат показывает наличие автокорреляции случайного возмущения в модели FE. Одной из причин автокорреляции является ошибка спецификации модели. К сожалению, в моделях (4), (5), (6) присутствует проблема эндогенности регрессоров, и применение «статического» аппарата моделей для панельных данных приводит к смещённым и несостоятельным оценкам, поскольку лаговое значение эндогенной переменной 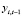 коррелирует с индивидуальным (фиксированным или случайным) эффектом μi, т.е. ни внутригрупповое (6), ни межгрупповое преобразования переменных не исключают проблему эндогенности.
коррелирует с индивидуальным (фиксированным или случайным) эффектом μi, т.е. ни внутригрупповое (6), ни межгрупповое преобразования переменных не исключают проблему эндогенности.
Спецификация динамической модели, с учетом индивидуального эффекта, может быть записана следующим образом:
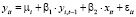 , (11)
, (11)
где yit – текущее значение объёмов золота в золотовалютных резервах i-й страны, 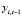 – лаговое значение объёмов золота в золотовалютных резервах i-й страны, xit – текущее значение ВВП страны. Для корректировки моделей с эндогенными регрессорами используется метод инструментальных переменных МИП [13, 14]. Для выбора инструмента для лагового регрессора
– лаговое значение объёмов золота в золотовалютных резервах i-й страны, xit – текущее значение ВВП страны. Для корректировки моделей с эндогенными регрессорами используется метод инструментальных переменных МИП [13, 14]. Для выбора инструмента для лагового регрессора 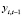 выполним следующие преобразования модели (11). Избавимся от индивидуальных эффектов путем перехода к первым разностям переменных
выполним следующие преобразования модели (11). Избавимся от индивидуальных эффектов путем перехода к первым разностям переменных
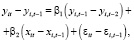
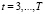 . (12)
. (12)
Из спецификации (12) следует, что
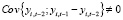 ,
,
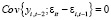 ,
,
т.е. лаговая переменная 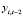 может быть выбрана в качестве инструментальной переменной для регрессора
может быть выбрана в качестве инструментальной переменной для регрессора 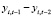 . Регрессор
. Регрессор 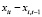 – экзогенный, поэтому может быть использован инструментом для самого себя. МИП-оценка параметров модели (12) в матричной форме имеет вид
– экзогенный, поэтому может быть использован инструментом для самого себя. МИП-оценка параметров модели (12) в матричной форме имеет вид
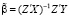 , (13)
, (13)
где Z – матрица инструментальных переменных, X – матрица регрессоров, Y – вектор значений эндогенной переменной. Структура матриц МИП-оценки (13) для модели (12) представлена в табл. 2.
Таблица 1
Оценки параметров местоположения модели FE
|
Номер страны i |
Страна |
|
|
t-статистика |
|
1 |
Китай |
51,658 |
28,472 |
1,814 |
|
2 |
Германия |
–264,348 |
11,694 |
–2,367 |
|
3 |
США |
–431,583 |
241,356 |
–1,788 |
|
4 |
Россия |
21,402 |
26,746 |
0,800 |
|
5 |
Япония |
–166,763 |
35,976 |
–4,635 |
|
6 |
Франция |
–267,497 |
91,898 |
–2,911 |
|
7 |
Нидерланды |
–222,088 |
49,561 |
–4,481 |
|
8 |
Швейцария |
–408,438 |
78,278 |
–5,141 |
Таблица 2
Структура матриц МИП-оценки
|
Z – инструментальных переменных |
X – регрессоров |
Y – вектор эндогенных переменных |
||
|
Z1 |
Z2 |
X1 |
X2 |
Y |
|
|
|
|
|
|
|
|
||||
Получена следующая МИП-оценка (13) модели (12):
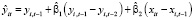 ,
, 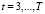 ,
, 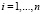 , (14)
, (14)
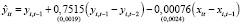 ,
, 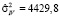 . (15)
. (15)
Обобщенная статистика Дарбина – Уотсона (10): DWp = 2,15, показывает отсутствие автокорреляции остатков в модели (14) с МИП-оценкой (15).
Использование инструментов Z в оценке (13) оправдано только в случае корреляции регрессоров с возмущениями модели. Если корреляция отсутствует (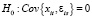 ), то МНК-оценки точнее МИП-оценок. Формальный тест, позволяющий определять, какой метод оценивания следует применять, это тест Хаусмана, основанный на сравнении оценок параметров в основной и альтернативной моделях. Статистика теста имеет вид квадратичной формы [15]:
), то МНК-оценки точнее МИП-оценок. Формальный тест, позволяющий определять, какой метод оценивания следует применять, это тест Хаусмана, основанный на сравнении оценок параметров в основной и альтернативной моделях. Статистика теста имеет вид квадратичной формы [15]:
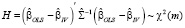 , (16)
, (16)
где m – число инструментов, 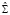 – оценка автоковариационной матрицы вектора
– оценка автоковариационной матрицы вектора 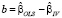 , которая в рамках нулевой гипотезы принимает вид
, которая в рамках нулевой гипотезы принимает вид
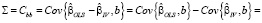
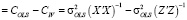 ,
,
так как
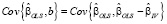
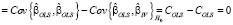 ,
,
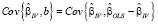
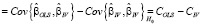 .
.
Таблица 3
Оценка автоковариационных матриц статистики Хаусмана
|
МНК-оценка |
МИП-оценка |
||
|
|
|
||
|
0,0054 |
0,0000606 |
0,00000372 |
–0,00000157 |
|
0,0000606 |
0,00000588 |
–0,00000157 |
0,00000587 |
При справедливости 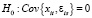 ,
,
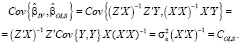
Используя в качестве оценки дисперсии возмущения 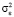 оценку, вычисленную по остаткам обычного МНК –
оценку, вычисленную по остаткам обычного МНК – 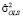 (МНК-оценка более устойчива к слабым инструментам), вычислим оценки автоковариационных матриц
(МНК-оценка более устойчива к слабым инструментам), вычислим оценки автоковариационных матриц 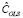 ,
, 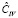 . Результаты оценивания приведены в табл. 3.
. Результаты оценивания приведены в табл. 3.
Результат тестирования: 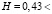
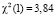 , следовательно, для исследуемых панельных данных можно использовать обычный МНК для спецификации (14), который дает более точные результаты, чем МИП:
, следовательно, для исследуемых панельных данных можно использовать обычный МНК для спецификации (14), который дает более точные результаты, чем МИП:
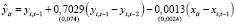 ,
, 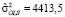 . (17)
. (17)
Построенная модель может быть улучшена посредством увеличения рассматриваемого временного периода и расширения как перечня наблюдаемых объектов (стран), так и перечня влияющих факторов. Периодическое тестирование на обновленных панельных данных решает задачи актуализации построенных моделей и возможности построения более точных прогнозов.




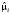
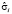
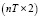 – матрица
– матрица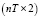 – матрица
– матрица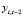
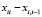
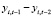
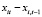
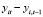
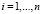 ,
,