Экономико-математические модели предприятия, отвечающие неоклассической концепции рыночной эффективности, достаточно подробно представлены в работах зарубежных [1, 2] и отечественных [3–5] авторов. Казалось бы, основные вопросы теории моделирования и оценки эффективности производственной корпорации решены (достаточно сослаться на фундаментальные работы Г.Б. Клейнера [3]). Однако интерес к экономико-математическим приложениям неоклассической микроэкономики с годами не ослабевает. В подтверждение этого тезиса достаточно указать на приведенные в списке литературы работы отечественных авторов, в которых затрагиваются те или другие теоретические аспекты выбора рыночной стратегии предприятия. В ряду теоретически значимых определенный интерес представляет проблематика сравнительной оценки эффективности моно- и многопродуктовой фирм, функционирующих в условиях конкурентных товарных и финансовых рынков.
«Неоклассическая» модель монопродуктовой фирмы и концепция эффективности затрат для условий конкурентных товарных и материальных рынков
В неоклассической микроэкономике фирма является базовой единицей анализа эффективности операционной и других видов рыночной деятельности производственной корпорации и рентабельности привлекаемого в финансирование переменных и постоянных активов собственного (акционерного) и заемного капитала. В основе неоклассической теории производства лежит концепция предельной отдачи производственных активов – элементов рабочего капитала предприятия и отдельных факторов (производственных ингредиентов), объясняющая рыночные процессы исключительно с позиции внешнего взаимодействия агентов рынка безотносительно к внутрикорпоративным факторам и мотивам деятельности менеджеров, собственников и инвесторов. В неоклассической теории предприятие – «черный ящик», описываемый производственной функцией (представленной в аналитической, табличной, сетевой и других формах), связывающей потоки производственных факторов-затрат переменных и постоянных активов на входе и товарные потоки – на выходе.
Фундаментальная отправная точка неоклассического подхода к анализу эффективности производства – функциональная зависимость, существующая между производственными издержками (в дальнейшем под издержками (производственными и внепроизводственными) будем понимать затраты переменных и постоянных ресурсов, не детализированные по объектам производства и по местам возникновения [6]) и конечным продуктом за анализируемый период. Выведем эту зависимость, опираясь на указанные базисные положения неоклассической концепции производства. Рассмотрим модель «выпуск – затраты» для монопродуктовой фирмы в изложении одного из авторов [7–9].
Пусть вектор 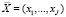 определяет набор производственных факторов (ПФ), агрегированных в группы по технологической принадлежности, причем j-я компонента вектора
определяет набор производственных факторов (ПФ), агрегированных в группы по технологической принадлежности, причем j-я компонента вектора 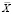 характеризует объем ПФ j-й группы, оцениваемый в натуральном выражении. Если pj – рыночная цена единицы j-го ПФ, то полная стоимость используемого набора ПФ совпадает с величиной
характеризует объем ПФ j-й группы, оцениваемый в натуральном выражении. Если pj – рыночная цена единицы j-го ПФ, то полная стоимость используемого набора ПФ совпадает с величиной 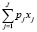 .
.
Если производственная функция (функция выпуска) 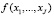 неубывающая в технологической области предприятия (области возможных наборов ПФ), а её полный образ для каждого объема выпуска Q аппроксимируется гладкой изоквантой (достаточно первого порядка гладкости), то аналитическая зависимость между полными затратами и объемом производства монопродукта может быть получена как решение следующей оптимизационной задачи:
неубывающая в технологической области предприятия (области возможных наборов ПФ), а её полный образ для каждого объема выпуска Q аппроксимируется гладкой изоквантой (достаточно первого порядка гладкости), то аналитическая зависимость между полными затратами и объемом производства монопродукта может быть получена как решение следующей оптимизационной задачи:
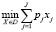 ,
, 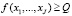 ,
,
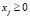 ,
, 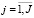 , (1)
, (1)
где D – технологическая область предприятия; Q – заданный объем выпуска (если функция выпуска оценивается величиной выпуска в стоимостном выражении, то Q – валовый доход).
Составим функцию Лагранжа для задачи (1):
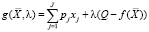 и приравняем к нулю частные производные по переменным xj, λ. Получим систему уравнений для определения решения
и приравняем к нулю частные производные по переменным xj, λ. Получим систему уравнений для определения решения  задачи (1):
задачи (1):
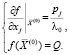
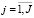 . (2)
. (2)
Так как заданному объему выпуска при сделанных предположениях относительно функции производства в технологической области предприятия соответствует только одна изокванта, можно сделать вывод о том, что решение задачи (1) для каждого объема производства Q единственное, т.е. 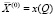 задает зависимость между объемом производства Q и минимальным по стоимости набором
задает зависимость между объемом производства Q и минимальным по стоимости набором 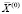 ПФ. Обозначим функцию полных затрат c(Q):
ПФ. Обозначим функцию полных затрат c(Q):
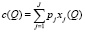 . (3)
. (3)
Так, в силу (2) 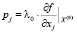 , то
, то 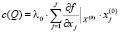 и, таким образом, c(Q) можно представить в виде
и, таким образом, c(Q) можно представить в виде
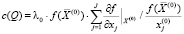 . (4)
. (4)
Сумма в правой части (4) совпадает с выражением для суммарной эластичности функции производства 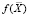 в точке
в точке 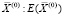 .
.
С учетом (4) запишем аналитическую зависимость между функцией издержек и функцией выпуска:
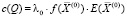 . (5)
. (5)
Так как в соответствии с (2), 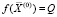 , то
, то
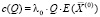 . (6)
. (6)
Полученное соотношение, связывающее величину производственных издержек в модели монопродуктового производства с величиной выпуска, позволяет получить следующие количественные характеристики функции полных затрат:
средние затраты:
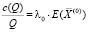 , (7)
, (7)
предельные затраты: 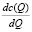 :
:
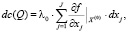
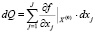 (8)
(8)
(соотношение (8) получается из соотношения (3), если дополнительно учесть, что 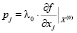 ).
).
Таким образом,
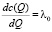 . (9)
. (9)
Соотношение (9) непосредственно указывает на экономическое содержание множителя Лагранжа оптимизационной задачи (1): λ0 совпадает с предельными издержками для заданного объема выпуска Q.
С учетом соотношения (9) перепишем формулу (7) в следующем виде:
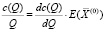 . (10)
. (10)
Последнее соотношение позволяет получить аналитическую зависимость для показателя эластичности полных затрат по выпуску:
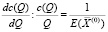 . (11)
. (11)
Таким образом, в модели монопродуктовой фирмы эластичность полных затрат по выпуску – величина, обратная суммарной эластичности выпуска по производственным факторам.
Широко известно и в ряде научных публикаций (например, [1, 4, 7]) отмечен факт снижения отдачи переменного ресурса с ростом объема Q выпуска для предприятий с серийным характером производства. В этом случае масштаб производства монопродуктовой фирмы характеризуется соотношением 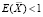 для возможных наборов ПФ из технологической области D. Эластичность затрат переменного ресурса для такого производства больше 1 (издержки растут быстрее, чем выпуск).
для возможных наборов ПФ из технологической области D. Эластичность затрат переменного ресурса для такого производства больше 1 (издержки растут быстрее, чем выпуск).
Этот вывод – отправная точка неоклассической теории эффективности монопродуктового производства, убедительно демонстрирует факт существенной зависимости эффективности производственной деятельности предприятия от объемов потребляемых постоянных и переменных ресурсов и уровня цен товарных рынков и рынков производственных факторов.
Проблематика декомпозиции и представления многопродуктовой фирмы как совокупности монопродуктовых
Выше отмечено, что идея представить многопродуктовое предприятие как некоторую взаимосвязанную применяемыми технологиями совокупность однопродуктовых предприятий получила широкое распространение и была взята «на вооружение» многими авторами. Сошлемся на наиболее цитируемые в этой области теоретических исследований экономики и управления предприятием работы [2, 10]. Наиболее простой случай многопродуктового предприятия связан с набором технологий, обеспечивающих выпуск товарной продукции в заданном ассортиментном соотношении. Исследования зависимости «выпуск – затраты» для такого предприятия, как правило, инициируются поиском точки безубыточного производства и оценкой риска убытков в случае резких колебаний рыночной конъюнктуры.
Проблематика определения точки безубыточности для монопродуктового, но многоассортиментного предприятия (например, предприятия агросферы, лесопереработки и др.) рассмотрена в работе авторов [7]. В ряду выпускаемых таким предприятием продуктов 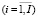 выделяют базовый xб и к нему «привязывают» объемы продукции другой номенклатуры с использованием основного соотношения многоассортиментного предприятия:
выделяют базовый xб и к нему «привязывают» объемы продукции другой номенклатуры с использованием основного соотношения многоассортиментного предприятия:
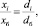 (12)
(12)
где xi, xб – объемы производства соответственно i-го 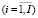 и базового изделий; di, dб – доли в общем объеме выпускаемой продукции (в натуральном выражении) соответственно i-го и базового изделий.
и базового изделий; di, dб – доли в общем объеме выпускаемой продукции (в натуральном выражении) соответственно i-го и базового изделий.
На основе следующих соотношений определим минимальный объем многоассортиментного производства, «привязанный» к базовому изделию:
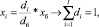 (13)
(13)
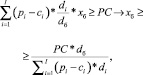 (14)
(14)
где PC – условно-постоянные затраты многоассортиментного предприятия.
Рассмотрим также модель, предложенную Л.Ф. Васильевой и М.В. Маничкиной [6], основанную на данных о доле выпуска каждого вида продукции в общем объеме производства.
Если для случая с одним продуктом в расчетах критического объема производства учитываются удельные переменные затраты и маржинальный доход, то для многопродуктового случая авторы предлагают оценить общую точку безубыточности с использованием средневзвешенного удельного маржинального дохода, а затем на основе данных о долях выпуска определить критические объемы производства для каждого вида продукции:
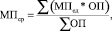 (15)
(15)
где МПср – средневзвешенный удельный маржинальный доход, руб.; МПед – маржинальный доход на ед. продукции, руб.; ОП – объем производства, ед.
Точка безубыточности в работе [6] рассчитывается по формуле:
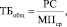 (16)
(16)
где ТБобщ – «общая» точка безубыточности, шт.; РС – величина условно-постоянных затрат, руб.; МПср – удельный средневзвешенный маржинальный доход, руб.
Далее частные точки безубыточности находим путем умножения общей точки безубыточности на долю оцениваемого вида продукции в общем объеме продаж:
ТБед = ОПед %*ТБобщ, (17)
где ТБед – «частная» точка безубыточности для оцениваемого продукта, шт.; ОПед, % – удельный вес оцениваемого продукта в общем объеме реализации, шт.; ТБобщ – «общая» точка безубыточности, шт.
Рассмотренные выше модели оценки точки безубыточности для случая многопродуктового производства в целом не отражают его особенности, одной из которых является способ учета специфического риска конкретного продукта. Корректный учет риска возможен для всего портфеля продуктов и в условиях достоверной информации о рыночных спросе и ценах.
Для иллюстрации возможного способа учета риска в моделях многономенклатурного предприятия приведем пример из работы авторов [7], в которой представлен следующий вариант:
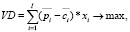 (18)
(18)
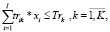 (19)
(19)
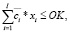 (20)
(20)
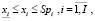 (21)
(21)
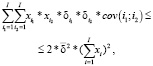 (22)
(22)
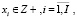 (23)
(23)
где VD – значение валового дохода; I – число изделий производственной программы; i, i1, i2 – индексы изделий производственной программы; 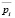 ,
, 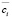 – средние за наблюдаемый период соответственно рыночная цена и удельные переменные затраты на производство i-го изделия;
– средние за наблюдаемый период соответственно рыночная цена и удельные переменные затраты на производство i-го изделия; 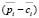 – планируемый удельный маржинальный доход реализации i-го изделия; K – число технологических операций, учитываемых в модели; trik – технологическая трудоемкость производства i-го изделия на k-й операции; Trk – эффективное время работы оборудования на k-й операции; OK – оборотный капитал, авансируемый в покрытие переменных затрат производственной деятельности;
– планируемый удельный маржинальный доход реализации i-го изделия; K – число технологических операций, учитываемых в модели; trik – технологическая трудоемкость производства i-го изделия на k-й операции; Trk – эффективное время работы оборудования на k-й операции; OK – оборотный капитал, авансируемый в покрытие переменных затрат производственной деятельности; 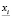 – минимальный (технологически обоснованный) объем производства i-го изделия; Spi – рыночный спрос на i-е изделие; δi – дисперсия маржинального дохода продукции i-го вида за период наблюдения; cov(i1; i2) – ковариация доходностей продукции с индексами i1 и i2 за период наблюдения;
– минимальный (технологически обоснованный) объем производства i-го изделия; Spi – рыночный спрос на i-е изделие; δi – дисперсия маржинального дохода продукции i-го вида за период наблюдения; cov(i1; i2) – ковариация доходностей продукции с индексами i1 и i2 за период наблюдения;  – пороговое значение риска производственной программы.
– пороговое значение риска производственной программы.
Экзогенными параметрами модели (18)–(23) являются параметры, определяемые рыночной конъюнктурой: 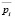 ,
, 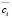 , Spi. Эндогенными (управляемыми) параметрами являются:
, Spi. Эндогенными (управляемыми) параметрами являются: 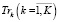 , OK,
, OK,  . Для фиксированных значений экзогенных параметров решение оптимизационной задачи (3)–(8) – вектор
. Для фиксированных значений экзогенных параметров решение оптимизационной задачи (3)–(8) – вектор 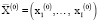 – позволяет определить финансовый результат производственной сферы предприятия как значение критерия
– позволяет определить финансовый результат производственной сферы предприятия как значение критерия 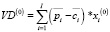 . Точка безубыточности многономенклатурного производства определяется из условия
. Точка безубыточности многономенклатурного производства определяется из условия
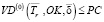 . (24)
. (24)
Для многономенклатурного предприятия соответствующую критическому уровню производства производственную программу 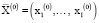 авторами предложено определить как решение задачи (18)–(23) с критерием, значение которого удовлетворяет условию (24).
авторами предложено определить как решение задачи (18)–(23) с критерием, значение которого удовлетворяет условию (24).
Негативной особенностью моделей декомпозиции многопродуктовой фирмы на ряд монопродуктовых (в частности, и модели (18)–(23) является «точечный» характер используемых в модели многопродуктового предприятия оценок ресурсоемкости изделий производственной программы и предположение о аддитивном (конкретно, линейном) характере совокупных производственных затрат, Это предположение не в полной мере соответствует даже случаю серийного производства и абсолютно не отражает особенности мелкосерийного и поточного производства, в условиях которых разнородная продукция критично отличается временем и технологиями обработки [2, 5, 10]. И, наконец, такой подход не отражает основную особенность многопродуктовой фирмы – зависимость затрат условно-постоянных активов от интенсивности конкретных технологических процессов в условиях многовариантности производственной программы и комбинаций (вариантов) ее реализации. Эта особенность многопродуктовой фирмы отмечена в работах Г.Б. Клейнера, А.В. Мищенко и М.А. Халикова [3, 4, 11]. В работе [4] предложен возможный подход к моделированию многопродуктовой фирмы. Рассмотрим его более подробно.
«Неоклассическая» модель многопродуктового предприятия и оценка эффективности затрат многономенклатурного производства
Для формального описания модели многономенклатурного предприятия введем следующие обозначения параметров и переменных:
i(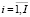 ) – индекс продукта;
) – индекс продукта;
xi – планируемый объем выпуска i-ого продукта (в натуральном выражении);
J(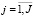 ) – индекс актива, учитываемого в калькуляции прямых переменных затрат операционной деятельности;
) – индекс актива, учитываемого в калькуляции прямых переменных затрат операционной деятельности;
wi – цена единицы j-го переменного актива, учитываемая в калькуляции прямых переменных затрат операционной деятельности текущего производственно-коммерческого цикла;
pi – цена реализации i-го продукта по завершении текущего производственно-коммерческого цикла;
yij – объем j-го переменного актива, предназначенного для производства i-го продукта;
fi – одно – однозначное отображение в первом ортанте I + J – мерного евклидова пространства (производственная функция) множества комбинаций возможных (в рамках рассматриваемого производственно – технологического процесса) наборов {yij} переменных активов в объемы {xi} производимых продуктов:
хi = 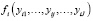 , (25)
, (25)
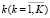 – индекс основного (внеоборотного) актива, учитываемого в калькуляции условно-постоянных затрат операционной деятельности пропорционально объемам и «технологической» сложности включаемых в производственную программу предприятия продуктов;
– индекс основного (внеоборотного) актива, учитываемого в калькуляции условно-постоянных затрат операционной деятельности пропорционально объемам и «технологической» сложности включаемых в производственную программу предприятия продуктов;
vk – цена реновации или амортизируемая стоимость единицы k-го постоянного актива, учитываемая в калькуляции условно-постоянных затрат операционной деятельности текущего производственно-коммерческого цикла;
φk – одно – однозначное отображение в I-мерном евклидовом пространстве (функция условно-постоянных затрат) множества допустимых в данных производственно-технологических условиях производственных программ {xi} в объемы zk k-ого постоянного актива (в натуральных единицах производственной мощности):
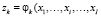 ), (26)
), (26)
Zk – величина k-го основного (внеоборотного) актива учитываемая в производственно-технологических отношениях операционной сферы предприятия (в натуральных единицах производственной мощности);
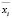 – максимальный объем реализации – ограничение на величину рыночного спроса на i-й продукт при цене реализации pi (
– максимальный объем реализации – ограничение на величину рыночного спроса на i-й продукт при цене реализации pi (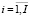 );
);
OA – ликвидные оборотные активы (формируемые на основе собственного капитала и краткосрочных заимствований), направляемые в покрытие прямых переменных затрат операционной деятельности текущего производственно-коммерческого цикла;
Fn – фиксированные затраты операционной сферы предприятия, включая страховой резерв.
Если не учитывать особенности и специфические производственно-технологические условия многопродуктовой фирмы (последовательность запуска изделий производственной программы, интенсивность технологических переходов, частоты переналадок оборудования и прочее), то статическая (для выбранного производственно-коммерческого цикла) упрощенная (без учета рыночного риска и риска структуры капитала) модель предприятия может быть представлена следующими соотношениями:
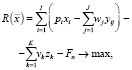 (27)
(27)
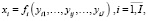 (25')
(25')
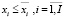 , (28)
, (28)
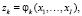
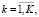 (26')
(26')
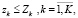 (29)
(29)
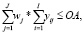 (30)
(30)
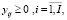
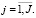 (31)
(31)
Приведем некоторые комментарии к модели (27), (25’), (28), (26’), (29)–(31).
Существенное отличие моделей одно- и многопродуктовой фирм заключается в наличии у последней ограничений (25’), (26’), определяющих зависимость объемов соответственно выпускаемой продукции и условно-постоянных затрат от планируемого распределения переменных активов по изделиям производственной программы. Для многопродуктовой фирмы в условиях производственно-технологических отличий выпускаемых продуктов вектора удельных переменных затрат 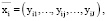
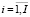 уникальные (отличные для неоднородных по технологии изготовления продуктов многопрофильной фирмы), что гарантирует одно – однозначность производственных функций {fi} и функций условно-постоянных затрат {φk} (
уникальные (отличные для неоднородных по технологии изготовления продуктов многопрофильной фирмы), что гарантирует одно – однозначность производственных функций {fi} и функций условно-постоянных затрат {φk} (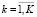 ).
).
Если в качестве исходного рассматривать вектор 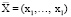 планируемой производственной программы, то на основе обратной зависимости
планируемой производственной программы, то на основе обратной зависимости 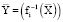 можно восстановить элементы прямоугольной матрицы прямых переменных затрат
можно восстановить элементы прямоугольной матрицы прямых переменных затрат 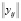 (
(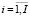 ,
, 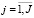 ) и использовать их далее в формальной записи критерия (27). В приведенной модели выбран именно этот подход, который условно назовем «традиционным».
) и использовать их далее в формальной записи критерия (27). В приведенной модели выбран именно этот подход, который условно назовем «традиционным».
Большой интерес, однако, представляет двойственная к традиционной модель оптимального распределения переменных активов по планируемым к выпуску продуктам, которая позволяет рассчитать и далее в задачах управления операционной сферой предприятия эффективно использовать двойственные оценки ограничений (29)–(31).
Рассмотрим эту задачу при дополнительном предположении о непрерывной дифференцируемости функций fi и φk (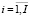 ,
, 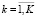 ). Составим функцию Лагранжа для модели (20), (18’), (21), (19’), (22)–(24), которая в условиях сделанных предположений представляет собой модель нелинейного выпуклого программирования:
). Составим функцию Лагранжа для модели (20), (18’), (21), (19’), (22)–(24), которая в условиях сделанных предположений представляет собой модель нелинейного выпуклого программирования:
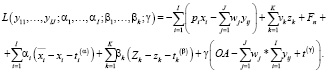 (32)
(32)
В силу монотонности функций fi и φk (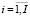 ,
, 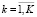 ) функционал (27) рассматриваемой модели является выпуклой непрерывно дифференцируемой функцией, что обеспечивает выполнимость условий теоремы Куна – Таккера о наличии седловой точки функции Лагранжа (32), которая может быть определена на основе соотношений (33)–(39):
) функционал (27) рассматриваемой модели является выпуклой непрерывно дифференцируемой функцией, что обеспечивает выполнимость условий теоремы Куна – Таккера о наличии седловой точки функции Лагранжа (32), которая может быть определена на основе соотношений (33)–(39):
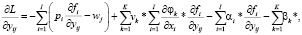
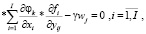
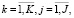 (33)
(33)
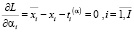 , (34)
, (34)
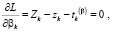
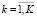 , (35)
, (35)
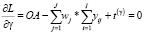 , (36)
, (36)
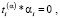
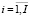 , (37)
, (37)
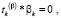
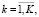 (38)
(38)
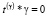 . (39)
. (39)
Если набор 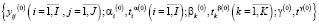 является решением системы уравнений (33)–(39), то он позволяет, во-первых, определить оптимальную по критерию (27) программу многопродуктовой фирмы
является решением системы уравнений (33)–(39), то он позволяет, во-первых, определить оптимальную по критерию (27) программу многопродуктовой фирмы 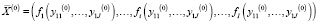 , а во-вторых, двойственные оценки
, а во-вторых, двойственные оценки 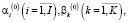
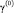 ограничений (28)–(30) (соответственно на: рыночный спрос, величины внеоборотного и оборотного капитала операционной сферы предприятия).
ограничений (28)–(30) (соответственно на: рыночный спрос, величины внеоборотного и оборотного капитала операционной сферы предприятия).
Например, эффективность (рентабельность) переменных активов в точке оптимального выпуска можно рассчитать на основе следующих выражений.
Пусть Δyij – прирост j-го переменного актива, направляемый в производство i-го продукта. Переходя к бесконечно малым величинам и заменяя Δyij на dyij, получим следующие выражения для приростов dx (вектора продуктов), dR (валового дохода в операционной сфере) и dc (валовых прямых переменных затрат):
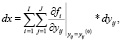 (40)
(40)
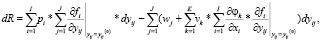 (41)
(41)
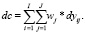 (42)
(42)
Для расчета рентабельности переменных активов в точке оптимального выпуска 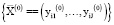 используем следующее выражение:
используем следующее выражение:
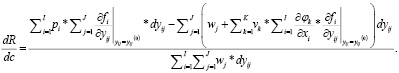 (43)
(43)
Заключение
В работе приведены описания авторских моделей одно- и многопродуктового предприятия. Авторы старались выдержать «неоклассический» подход при описании «вход-выходных» параметров модели. Важным результатом исследования особенностей моделирования одно- и многопродуктовой фирмы является вывод о существенном влиянии номенклатурного состава производственной программы на зависимость динамики «затраты – выпуск» и на рентабельность как полного рабочего капитала, так и отдельно его переменной и условно-постоянной составляющих. Этот результат является новым в неоклассической теории фирмы и в определенной степени дополняет результаты известных работ Р. Солоу [12] и Г.Б. Клейнера [3].



