Для обеспечения устойчивого развития любого предприятия необходимо глубокое понимание управленческих процессов, применение адекватных алгоритмов выработки управленческих решений и контроля основных показателей эффективности. Этого невозможно добиться, если не учитывать абстрактную природу многих процессов в экономике. Управление бизнес-процессом, качеством продукции, финансами – на самом деле во всех этих случаях объект управления абстрактный, существующий в виде образа или, если выражаться математическим языком – отображения. Эти объекты управления не подвержены реальным воздействиям (качества продукции, например, невозможно добиться, отдавая ему приказы или поощряя его материально). Алгоритмы организации управления в таких случаях и есть предмет исследования данной работы.
Теория
Процесс управления реализуется в системе управления, схема которой изображена на рис. 1.
Здесь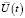 
– вектор управляющих воздействий, 
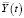– вектор управляемых величин, 
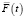– вектор возмущающих воздействий.
В этой схеме выполняется алгоритм подачи реальных управляющих воздействий на реальный объект управления с целью обеспечить необходимые его состояние или поведение. Обычно управление осуществляется либо объектом (явлением), либо процессом. В первом случае, при управлении важны свойства неживых объектов или качества живых или их состояния. Во втором, при управлении процессами, важны показатели процесса (например, технологические режимы), логика его протекания (стадии или этапы), погрешности и отклонения.
Абстрактный объект в классической теории управления появляется над системой управления, как представлено на рис. 2. Математически подобная задача сводится к классической задаче оптимального управления абстрактным объектом [1]. Здесь получается двухуровневая и двухконтурная схема. Первый контур и, соответственно, нижний уровень реализует непосредственное управление реальным объектом (левая часть схемы), на втором уровне и во втором контуре осуществляется оценка функционала и решается задача оптимального управления. В определенном смысле можно говорить об управлении функционалом с целью его минимизации.
Алгоритмы управления коренным образом меняются, когда объект управления будет абстрактным. Схема управления в этом случае изменяется, как показано на рис. 3. У абстрактного объекта управления всегда есть «материальный носитель», на который можно подавать реальные управляющие воздействия, реализуя косвенное управление, а состояние абстрактного объекта является в этом случае гомоморфным отображением (образом) [2] каких-то качеств или свойств, показателей материального носителя, и в этом его принципиальное отличие от модели объекта, которая должна реализовывать и все процессы, протекающие в моделируемом объекте. «Гомоморфизм – это приблизительный изоморфизм (изоморфизм – взаимно-однозначное соответствие между элементами двух абстрактных множеств, сохраняющее все свойства элементов этих систем и все отношения между ними). Изоморфизм означает тождество, подобие, одинаковость строения. Такое подобие предполагает равночисленность, так как если исследуемые совокупности имеют разные мощности, то они будут иметь и разное строение [3, 4]. Гомоморфный образ содержит не большее число элементов, чем оригинал, но элементами его могут быть классы индивидов, являющихся элементами прообраза. Основная цель гомоморфного преобразования состоит в том, чтобы «свернуть» всю доступную информацию об исследуемых объектах (явлениях, процессах) в более компактную, удобно обрабатываемую форму. Универсальных алгоритмов такого преобразования в настоящее время нет» [2]. Математически это отображение можно выразить оператором отображения, как показано на схеме (рис. 3).
Материальный носитель и абстрактный объект должны рассматриваться вместе, как единое целое, образуя единый контур управления [5]. Только в этом случае и можно говорить об управлении абстрактным объектом. При этом возникает несколько вопросов.
Первый вопрос связан с оценкой управляемой величины в данном случае она же отражает состояние абстрактного объекта. Эта оценка будет простой, если оператор детерминированный, например функционал от детерминированных величин. Представителем такого оператора может служить оператор оценивания себестоимости изготовления продукта (для удобства его вычисления представлять его можно в многомерном пространстве). Материальным носителем в этом случае будет конкретное производство с заданными технологическими операциями.
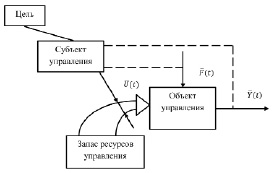
Рис. 1. Схема системы управления
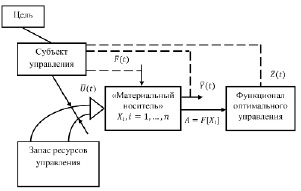
Рис. 2. Абстрактный объект – функционал оптимального управления
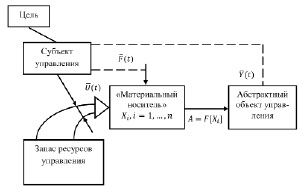
Рис. 3. Схема системы управления абстрактным объектом
Если состояние абстрактного объекта оценивается вероятностью, то встает вопрос – как управлять вероятностью? Повышать вероятность некоторого события возможно только созданием условий, благоприятствующих его появлению, и устранением причин его «непоявления». Примером является управление готовностью производства к запуску новой продукции. Оценить готовность можно вероятностью того, что в данный момент можно начать производство. Для повышения этой готовности необходимо разработать технологию, обеспечить производство всеми материалами, комплектующими, наконец, подготовить кадры [6]. В этом случае управление в значительной мере становится организационным. При этом под организационным управлением будем понимать «развернутую во времени совокупность процедур, позволяющую сформировать определенную целенаправленную систему деятельности. Каждая такая процедура вмешивается в налаженный или случайный ход событий, увеличивая вероятность возникновения события цели… Основу процесса организационного проектирования составляет разработка формально-логической модели предприятия, отвечающей целевым установкам» [1]. Вероятностный оператор в схеме на рис. 3 может также потребовать дополнительных специальных тестовых процедур, оценивающих вклад каждого из влияющих факторов и снижающих уровень автоматизации в схеме [7].
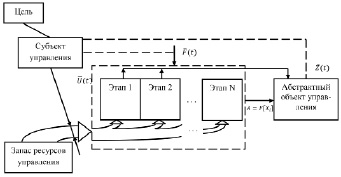
Рис. 4. Управление процессным абстрактным объектом
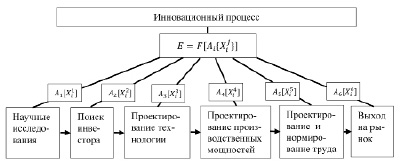
Рис. 5. Отображение инновационного процесса
Особые алгоритмы необходимы при управлении некоторым процессом, схема которого представлена на рис. 4. При этом количество отображающих операторов возрастает за счет разбиения основного процесса на части: этапы, стадии, подпроцессы, процедуры, операции. Кроме того, основной задачей верхнего уровня при управлении процессом становится задача оптимального перераспределения ресурса между частями этого процесса и прогнозирования [8]. Разумеется, и логика следования частей процесса, кроме последовательной, может быть разветвленной, а также с параллельной реализацией некоторых частей и последующим их схождением. При реализации схождения параллельно идущих частей процесса необходимо дополнительно решать задачу синхронизации, а иногда дополнять иерархией.
Подводя итог теоретическому исследованию, введем определение: управление абстрактным объектом будем понимать как применение управленческих алгоритмов к материальному носителю, отображением (образом) которого является состояние абстрактного объекта, изменяющих это состояние в направлении цели управления.
Материалы и методы исследования
Рассмотрим в качестве примера управления процессным абстрактным объектом алгоритмы управления инновационным процессом. Схема преобразования инновационного процесса в абстрактный объект представлена на рис. 5. Здесь изображены не только операторы преобразования информации о каждой стадии протекания инновационного процесса, но и логика контроля за этими стадиями, которая может быть не только последовательной, но предусматривать возвраты к предыдущим стадиям в случае необходимости.
Инновационный процесс начинается с проведения глубоких, поисковых научных исследований, позволяющих определить перспективный продукт, удовлетворяющий некую социальную потребность, которая может быть востребована на рынке. Вторым этапом проводится поиск инвестора. При успешном выполнении первых двух этапов необходимо организовать производство (тиражирование) выбранного продукта. Организация производства включает три этапа: проектирование конструкций и технологии изготовления продукта, проектирование производственных мощностей, проектирование и нормирование труда. Наконец, завершающим этапом является этап вывода продукта на рынок.
Если R – ресурсы, направляемые на управление процессом, то приращение эффективности инновационного процесса можно разложить по этапам его реализации:
(*)
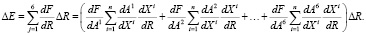Как видим, оценка эффективности инновационного процесса в данном линейном разложении свелась к определению функций влияния: параметров на эффективность, состояния подпроцессов на параметры и, наконец, вложенных ресурсов на состояние подпроцессов, их определение (например, экспертным методом) позволит оптимальным образом перераспределить ресурсы управляющих воздействий.
Результаты исследования и их обсуждение
Проведенное исследование показывает:
1. У абстрактного объекта управления всегда есть материальный носитель.
2. Состояние абстрактного объекта – гомоморфное отображение материального носителя.
3. Цель управления абстрактным объектом всегда связана с его состоянием.
Управление абстрактным объектом сводится к организационному управлению, алгоритмы которого преобразуют материальный носитель в направлении целевого изменения состояния этого абстрактного объекта.
Главной задачей общего алгоритма управления является ранжирование влияющих факторов и оптимальное перераспределение ресурсов между ними. В простейшем случае можно применить линейное разложение по формуле (*), в котором функции влияния могут быть определены экспертным методом.
Заключение
Таким образом, исследование алгоритмов управления абстрактным объектом позволяет сделать вывод о том, что для достижения целевого состояния абстрактного объекта необходимо организовывать материальный носитель и создавать адекватные условия, в которых он функционирует. При этом главной задачей общего алгоритма управления является ранжирование влияющих факторов и оптимальное перераспределение ресурсов между ними.