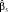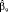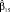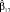Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Эконометрическое моделирование используется для решения различных прикладных задач. Но по конечным целям С.А. Айвазян выделяет две основные: «(а) прогноз экономических и социально-экономических показателей (переменных); (б) имитация различных возможных сценариев социально-экономического развития анализируемой системы, когда статистически выявленные взаимосвязи между характеристиками производства, потребления, социальной и финансовой политики и т.п. используются для прослеживания того, как планируемые (возможные) изменения тех или иных поддающихся управлению параметров производства или распределения скажутся на значениях интересующих нас «выходных» характеристик» [1]. При решении задач второго типа возможно использование многофакторных регрессионных моделей для выявления и ранжирования факторов по степени их влияния на результирующую переменную. В первую очередь при оценке влияния факторов на эндогенную переменную учитывают значения коэффициентов регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости [2].

Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности, бета-коэффициенты и дельта-коэффициенты [2].

Коэффициенты эластичности 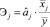позволят сравнивать факторы в процентах и могут быть вычислены не только для линейной функции. Коэффициенты эластичности показывают, на сколько процентов в среднем изменится зависимая переменная при изменении объясняющей переменной на один процент при фиксированных значениях других объясняющих переменных. Коэффициент эластичности не учитывает степень колеблемости факторов.

Для решения вопроса сравнения силы влияния факторов, имеющих разную степень колеблемости, используют бета-коэффициенты, или коэффициенты регрессии в стандартизованном виде: 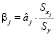. Стандартизованные коэффициенты сравнимы между собой, поэтому с их помощью можно ранжировать факторы по силе воздействия на результирующую переменную. Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения Sy изменится эндогенная переменная с изменением соответствующей экзогенной переменной xj на величину своего среднеквадратического отклонения при фиксированном значении остальных независимых переменных.

Перечисленные коэффициенты позволяют упорядочить факторы по степени влияния факторов на эндогенную переменную. Однако еще раз обратим внимание на важный момент – коэффициенты эластичности, бета-коэффициенты, как и коэффициенты регрессии, могут интерпретироваться только при условии, что остальные переменные в модели регрессии неизменны, когда изменение одной переменной не приводит к изменению других переменных [2].

При наличии мультиколлинеарности переменных по коэффициентам регрессии нельзя судить о влиянии этих переменных на функцию [3]. Существуют различные методы, направленные на выявление мультиколлинеарности: анализ матриц коэффициентов парной и частной корреляции, метод Фаррара – Глоубера [3], метод дополнительных регрессий, тесно связанный с методом инфляционных факторов (VIF) и другие. Выявление мультиколлинеарности с помощью VIF реализовано во многих программах, в том числе в R и Gretl [4].

Фактор инфляции дисперсии VIF (Variance Inflation Factor) показывает, во сколько раз увеличивается (вздувается) дисперсия коэффициента регрессии за счёт коррелированности регрессоров X1,…,Xk по сравнению с дисперсией этого коэффициента, если бы регрессоры были некоррелированы. Фактор инфляции дисперсии вычисляется по формуле

,

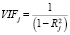где 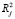– коэффициент детерминации j-го регрессора Xj, (j = 1,…,k, k – число факторов модели), по всем остальным регрессорам. Если фактор инфляции дисперсии равен единице, то это свидетельствует об ортогональности вектора значений признака остальным. Высокие значения фактора инфляции дисперсии соответствуют почти линейной зависимости j-го столбца от остальных, происходящей из-за высокой корреляции данных. Принято считать, что значение от 1 до 2 ( 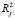от 0 до 0,5) означает, что включение Xj в модель не приводит к мультиколлинеарности.

Если VIF_j = 16, то стандартная ошибка оценки параметра βj в 4 раза 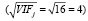превышает эту оценку, полученную при полном отсутствии мультиколлинеарности. Считается, что если 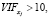то данный регрессор приводит к мультиколлинеарности. Недостатками этого критерия мультиколлинеарности является то, что он может принимать большие значения сразу для нескольких признаков, что мешает определить, какой из признаков необходимо удалить.

В программе Gretl представлен ещё один метод, основанный на вычислении собственных значений и собственных векторов матрицы XTX, позволяющий не только выявить мультиколлинеарность среди исходных регрессоров, но и определить переменные, которые показывают наибольшую вовлеченность в зависимости. Этот метод известен как метод Белсли [5]. В Gretl метод представлен как диагностика коллинеарности Belsley-Kuh-Welsch (BKW).

Если матрица XTX обратима, то

,

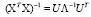где 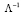– матрица, обратная к диагональной матрице собственных значений матрицы XTX, расположенных в порядке убывания; U – матрица, столбцами которой являются нормированные собственные векторы, то есть сумма квадратов координат каждого вектора равна 1.

Дисперсия коэффициента регрессии 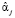равна

,

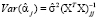где 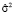– выборочная дисперсия остатков.

Вычислив диагональные элементы матрицы 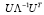, получаем представление oценки дисперсии параметров регрессии в виде суммы p слагаемых

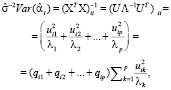
где λ_k – собственное число матрицы XTX; p – количество параметров в модели регрессии, λ1 > λ2 > … > λp,

q_ij – доля j-го собственного вектора в дисперсии i-го коэффициента регрессии :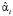

.

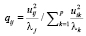Коэффициент (индекс) обусловленности η_j вычисляется по формуле

,

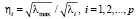где 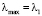– максимальное собственное число.

Для обнаружения мультиколлинеарности признаков в программе Gretl выдаются значения факторов инфляции дисперсии (Метод инфляционных факторов) и таблица диагностики коллинеарности Belsley-Kuh-Welsch [6] (табл. 1), в которой каждая строка соответствует своему индексу обусловленности η_j, а элементы строки – значения q_ij.. Сумма элементов по столбцам равна 1.

Большие величины η_j означают, что, возможно, есть зависимость между регрессорами. Большие значения qij в строках, соответствующих большим величинам η_j, относятся к регрессорам, между которыми эта зависимость существует.

Вопрос о том, какое значение коэффициента обусловленности считать большим, решается в каждом конкретном случае индивидуально, в зависимости от ценности информации, её объёма, целей и задач исследования. Часто значения коэффициента обусловленности считаются большими, если они больше 10 [7].

Относительно близкое к нулю λj приводит к большим коэффициентам обусловленности. Нулевое значение λj означает, что существует строгая мультиколлинеарность. Большие значения коэффициентов обусловленности свидетельствуют о наличии зависимостей; большие значения долевых коэффициентов qij внутри соответствующих строк указывают столбцы матрицы Х, участвующие в зависимостях.

Отметим также, что если больших коэффициентов обусловленности больше одного, то в зависимостях могут участвовать все переменные, которые имеют большие суммарные значения коэффициентов в последних строках таблицы с большими коэффициентами обусловленности.

Проиллюстрируем применение метода инфляционных факторов и метода Белсли для выявления и устранения мультиколлинеарности при решении задачи анализа значимости и степени влияния ряда традиционных показателей на переменную прибыль (убыток) до налогообложения ряда предприятий, относящихся к виду деятельности «Добыча сырой нефти» (Система СПАРК 13.12.2017 [8]). Была сделана выборка данных, представляющих финансовые показатели 186 фирм за 2016 г. В качестве регрессоров модели использованы более 20 переменных – среднесписочная численность работников, рентабельность активов, стоимость основных производственных средств и оборудования, стоимость совокупных активов, материальные активы и др.

Таблица 1

Разложение дисперсии коэффициентов регрессии

На основании собранных данных была построена эконометрическая линейная модель множественной регрессии. Анализ мультиколлинеарности, выполненный средствами пакета Gretl, показал наличие сильной мультиколлинеарности (табл. 2 и рис. 1). Из табл. 2 видно, что факторы Х2, Х7, Х15 имеют самые большие значения VIF, скорее всего именно эти факторы приводят к мультиколлинеарности [7].

Анализ диагностики мультиколлинеарности по методу Белсли, фрагмент которой приведен на рис. 1, показал, что наибольшему значению индекса обусловленности равному 6317,33 соответствуют факторы Х2, Х7, Х12, Х15 с большими значениями qij, между этими факторами существует тесная зависимость. Выявив с помощью метода Белсли переменные, участвующие в зависимости, удаляем из регрессионной модели одну из этих переменных. На первом шаге удаляем Х2. Затем параметры модели оцениваются заново. Если обнаружена другая зависимость, исключаем из модели одну из переменных второй группы и далее повторяем исследование на мультиколлинеарность. Через несколько шагов была получена модель, не содержащая коллинеарных факторов, все коэффициенты которой значимы (рис. 2 и 3):

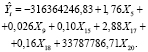
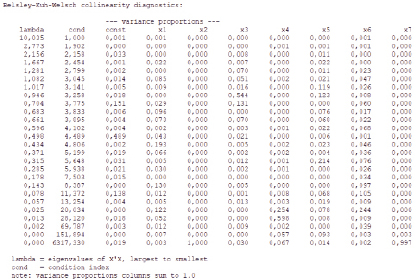
Рис. 1. Фрагмент диагностики коллинеарности по методу Белсли

Таблица 2

Значения инфляционных факторов

Рис. 2. Результат оценки параметров модели МНК

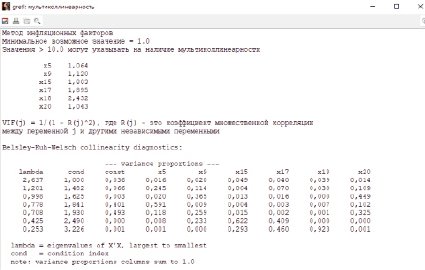
Рис. 3. Результат теста на мультиколлинеарность

В последнюю модель вошли следующие факторы: Х5 – Денежные средства, ед. RUB; Х9 – Займы и кредиты (долгосрочные), ед. RUB; Х15 – Краткосрочные обязательства, ед. RUB; Х17 – Нематериальные активы, ед. RUB; Х18 – Оборотные активы, ед. RUB; Х20 – Рентабельность активов (ROA), %. Коэффициент детерминации 0,865 и скорректированный коэффициент детерминации свидетельствуют о хорошем приближении модели исходным данным.

Анализ теста на мультиколлинеарность последней модели показал ее отсутствие. Значение факторов инфляции от 1 до 2,4; наибольшее значение индекса обусловленности 3,2 (рис. 3).

Избавившись от мультиколлинеарности, можно использовать полученное уравнение регрессии для оценки влияния факторов на зависимую переменную с помощью бета и дельта-коэффициентов Δ (j):

,

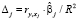где 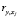– коэффициент парной корреляции между фактором Xj и зависимой переменной, R2 – коэффициент детерминации.

Дельта-коэффициент показывает долю влияния фактора в суммарном влиянии всех факторов [3]. Полученные результаты приведены в табл. 3, из которой можно сделать вывод, что наибольшее влияние на переменную прибыль (убыток) до налогообложения предприятий, относящихся к виду деятельности «Добыча сырой нефти» оказывает фактор Х18 – Оборотные активы (50,8 %), затем Х5 – Денежные средства (19,3 %) и Х17 – Нематериальные активы (15,4 %).

Таблица 3

Бета и дельта-коэффициенты

Таким образом, была решена задача ранжирования факторов по степени их влияния на результирующий показатель.