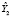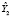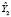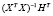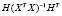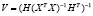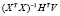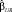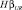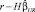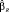Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Основная цель эконометрического моделирования – изучение взаимосвязей между переменными, описывающими экономические объекты. При моделировании простых экономических объектов используются отдельные изолированные уравнения парной или множественной регрессии. Для описания сложных экономических систем, включающих несколько экономических объектов, используются не отдельные уравнения, которых недостаточно для объяснения их функционирования, а системы уравнений. Возникает необходимость оценивания систем уравнений. Для этой цели в эконометрике разработаны специальные методы исследования и оценивания. Методы оценивания зависят от типа системы уравнений. Если исследуемая система включает независимые уравнения (система независимых уравнений), то каждое уравнение может рассматриваться самостоятельно, и для оценки его параметров, при условии выполнения всех предпосылок Гаусса – Маркова, можно использовать обычный метод наименьших квадратов (МНК, ordinary least squares method, OLS), при гетероскедастичном возмущении – метод взвешенных наименьших квадратов (weighted least squares method, WLS), при гетероскедастичности и/или автокорреляции – обобщенный метод наименьших квадратов (ОМНК, generalized least squares method, GLS) [1].

Если взаимосвязь уравнений объясняется только корреляцией их случайных возмущений (влиянием «одной экономической среды» на формирование переменных уравнения), то такая система называется системой внешне не связанных уравнений (Seemingly Unrelated Regression, SUR). Оценка параметров SUR выполняется в рамках обобщенного метода наименьших квадратов (ОМНК), применяемого к специальным образом составленной спецификации модели [2].

Если система состоит из набора взаимосвязанных уравнений, и одни и те же переменные в одних уравнениях являются эндогенными, а в других – регрессорами, то такие системы называют системами одновременных уравнений, СОУ (Simultaneous equations). СОУ чаще остальных систем используется в эконометрических исследованиях. Для оценки параметров СОУ используются: косвенный метод наименьших квадратов (КМНК, indirect least squares method, ILS), двухшаговый метод наименьших квадратов (ДМНК, two stage least squares method, 2SLS), которые позволяют решить проблему эндогенности переменных, возникающую при оценке структурных параметров системы. Повысить точность ДМНК-оценок структурных параметров можно в рамках трёхшагового метода наименьших квадратов (ТМНК, three stage least squares method, 3SLS), учитывающего взаимодействие уравнений в системе [3]. Рассмотрим методы оценки параметров СОУ на примере следующей модели [4]:

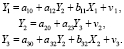(1)

Вектор эндогенных переменных системы (1) включает элементы: Y1 – объем продукции (в тыс. штук); Y2 – количество работающих (в тыс. человек); Y3 – стоимость основных фондов (в млн злотых), вектор экзогенных переменных: X1 – использованное сырьё (в тыс. тонн); X2 – инвестиции (в млн злотых). Данные за 11 лет приведены в табл. 1.

Проблема эндогенности регрессоров структурной формы спецификации (1) приводит к смещению МНК-оценок параметров модели. Поэтому для оценки параметров используются косвенный метод наименьших квадратов (КМНК) – для точно идентифицируемых уравнений модели, и двухшаговый метод наименьших квадратов (ДМНК) – для идентифицируемых уравнений. КМНК-оценки параметров точно идентифицируемых уравнений совпадают с ДМНК-оценками [5].

Косвенный метод наименьших квадратов. Алгоритм КМНК состоит из следующих шагов [6]:

1. По структурной форме модели

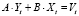, (2)

где

,

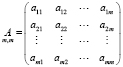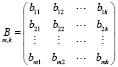
– матрицы структурных параметров, 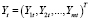– вектор-столбец значений эндогенных переменных, 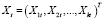– вектор-столбец значений предопределенных переменных, которые могут включать как экзогенные переменные (внешние по отношению к системе), так и лаговые значения эндогенных переменных, 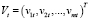– вектор-столбец случайных возмущений, t – номер наблюдения, строится приведенная форма (значком «Т» обозначена операция транспонирования):

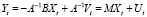, (3)

где

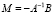(4)

– матрица коэффициентов приведенной формы,

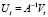
– вектор случайных возмущений приведенной формы.

2. Определяются МНК-оценки параметров приведенной формы (3).

3. По МНК-оценкам приведенной формы вычисляются оценки параметров структурной формы (2).

Для оценки структурных параметров по приведенным, на третьем шаге, используется уравнение взаимосвязи структурных и приведенных параметров (4):

,

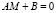которое можно записать через расширенную матрицу 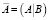структурной формы

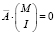, (5)

где I – единичная матрица k×k, где k – число предопределенных переменных в системе. Если значения элементов матрицы М приведенной формы неизвестны, то в системе (5) используются их МНК-оценки. Расширенная матрица структурных параметров для модели (1) имеет вид

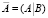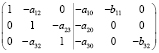= . (6)

Первое и третье уравнения системы (1) точно идентифицируемы, поэтому для них применим КМНК. Рассмотрим первое уравнение структурной формы. Его параметры, с учетом (6), удовлетворяют системе линейных уравнений (5)

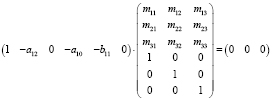
или

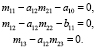(7)

Таким образом, КМНК-оценки структурных параметров первого уравнения системы (1) равны

,

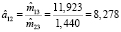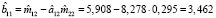, (8)

,

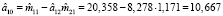где использованы МНК-оценки параметров приведенной формы, полученные по данным табл. 1:

, ,

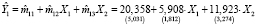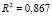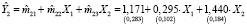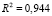, , (9)

, .

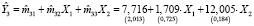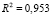Двухшаговый метод наименьших квадратов. В ДМНК, на первом шаге, оцениваются эндогенные регрессоры уравнения по всем предопределенным переменным модели. В первом уравнении структурной формы

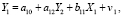(10)

– это Y2 (количество работающих). Оценка этой переменной выполняется в рамках второго уравнения приведенной формы (9). На втором шаге ДМНК, по оценкам 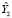и экзогенной переменной X1 (приведенных в табл. 2), находятся ДМНК-оценки параметров первого уравнения структурной формы:

.

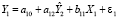Таблица 2

Результаты первого шага ДМНК

Из результатов оценивания следует, что КМНК-оценки параметров первого (точно идентифицируемого) уравнения структурной формы СОУ (8) совпадают с его ДМНК-оценками:

,

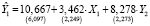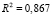. (11)

Метод инструментальных переменных (МИП). Для решения проблемы эндогенности используется метод инструментальных переменных, в котором в качестве инструментов, замещающих регрессоры, коррелирующие с возмущением, используются переменные (инструменты), сильно коррелирующие с данным регрессором, и не коррелирующие с возмущением модели. МИП-оценка параметров модели множественной линейной регрессии имеет вид [7]:

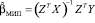, (12)

где Z – матрица инструментальных переменных. Задача выбора инструментальных переменных не всегда решается просто. Одним из способов является замена переменной на её оценку, полученную в рамках другой модели. Применительно к первому уравнению структурной формы СОУ (1), заменим переменную Y2 её оценкой, полученной в рамках модели приведенной формы (9). Элементы матриц регрессоров и инструментальных переменных приведены в табл. 3.

Таблица 3

Матрицы МИП-оценки

Результаты, полученные по формуле (12), совпадают с ДМНК-оценками. Таким образом, ДМНК является методом инструментальных переменных, нацеленным на корректировку эндогенности регрессоров модели.

Метод наименьших квадратов с ограничениями на параметры. Оценим параметры первого уравнения структурной формы (1) в рамках МНК с ограничениями на параметры. МНК-оценка параметров линейной модели множественной регрессии

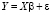(13)

с линейными ограничениями общего вида

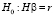, (14)

где Y – вектор значений эндогенной переменной (n*1), X – матрица регрессоров (n*k), β – вектор параметров (k*1), r – вектор констант ограничений (q*1), H – матрица ограничений (q*k), ranr(H) = q, q * k, определяется по формуле [8, 9]

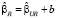, (15)

где 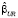– МНК-оценка параметров без учёта ограничений (unrestricted)

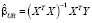, (16)

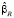– МНК-оценка параметров при наличии ограничений (restricted), b – коэффициент корректировки:

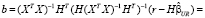
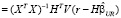, (17)

где

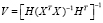. (18)

Оценка 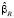параметров модели (13), (14) является решением задачи на условный экстремум:

, ,

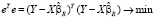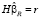где e – вектор остатков в модели с ограничениями на параметры. Оценим первое уравнение модели (1) МНК без учета ограничений:

,

.

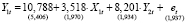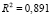МНК-оценки параметров:

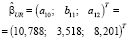
– смещенные и несостоятельные, в силу проблемы эндогенности. Для вычисления корректировочного члена (15), в качестве ограничений на параметры используем взаимосвязь (7) между структурными и приведенными параметрами, которую запишем в матричном виде:

.

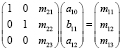При формировании матрицы ограничений H и вектора констант ограничений r воспользуемся МНК-оценками параметров приведенной формы (9):

,

.

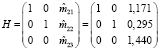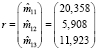В табл. 4 приведены значения матриц, используемых в формулах (15)–(18) в порядке, удобном для их вычисления.

Значения вектора оценок параметров без ограничений, ограничений в неявном виде, коэффициента корректировки, оценок параметров при наличии ограничений приведены в табл. 5.

Таблица 5

Вычисление оценок параметров с ограничениями

Сравнение результатов, приведенных в пятом столбце табл. 5, и оценок параметров модели (11) показывает, что оценки параметров структурного уравнения СОУ в рамках МНК с ограничениями (5) на структурные параметры совпадают с ДМНК-оценками, решающими проблему эндогенности.